Cách chứng minh đường thẳng vuông góc với mặt phẳng – bài tập có đáp án chi tiết

Cách chứng minh đường thẳng vuông góc với mặt phẳng – bài tập có đáp án

Phương pháp chứng minh đường thẳng vuông góc với mặt phẳng.

Để chứng minh đường thẳng a vuông góc với mặt phẳng (P) ta chứng minh:

– a vuông góc với hai đường thẳng cắt nhau nằm trong (P).

– a song song với đường thẳng b mà b vuông góc với (P).

Bài tập chứng minh đường thẳng vuông góc với mặt phẳng có đáp án chi tiết

Lời giải chi tiết

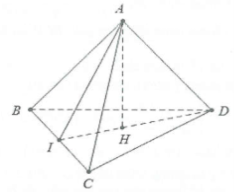
a) Do các tam giác ABC và BCD là hai tam giác cân nên tại A và D ta có: $\left\{ \begin{array}  {} AI\bot BC \\  {} DI\bot BC \\ \end{array} \right.$ (trong tam giác cân đường trung tuyến đồng thời là đường cao)

Do đó $BC\bot (ADI)$.

b) Do AH là đường cao trong tam giác ADI nên $AH\bot DI$

Mặt khác $BC\bot (ADI)\Rightarrow BC\bot AH$

Do đó $AH\bot (BCD)$

Lời giải chi tiết

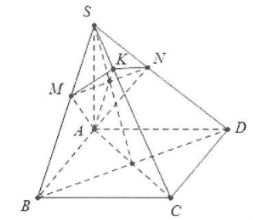
a) Do $SA\bot (ABCD)\Rightarrow SA\bot BC$

Mặt khác ABCD là hình vuông nên $BC\bot AB$

Khi đó $\left\{ \begin{array}  {} BC\bot AB \\  {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAB)$

Tương tự chứng minh trên ta có: $CD\bot (SAD)$

b) Do $BC\bot (SAB)\Rightarrow BC\bot AM$

Mặt khác $AM\bot SB\Rightarrow AM\bot (SBC)$

Tương tự ta có: $AN\bot (SCD)$

c) Do $\left\{ \begin{array}  {} AM\bot (SBC) \\  {} AN\bot (SCD) \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} AM\bot SC \\  {} AN\bot SC \\ \end{array} \right.\Rightarrow SC\bot (AMN)$

Hai tam giác vuông SAB và SAD bằng nhau có các đường cao tương ứng là AM và AN nên CM = DN. Mặt khác tam giác SBD cân tại đỉnh S nên MN//BD.

d) Do ABCD là hình vuông nên $AC\bot BD$, mặt khác $SA\bot BD\Rightarrow BD\bot (SAC)$

Do $MN//BD\Rightarrow MN\bot (SAC)\Rightarrow MN\bot AK$

Lời giải chi tiết

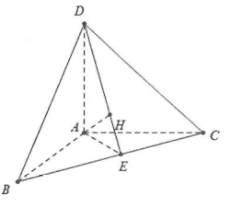
a) Gọi H là hình chiếu vuông góc của điểm A trên mặt phẳng (BCD) thì $AH\bot (BCD)$

Ta có $\left\{ \begin{array}  {} AD\bot AB \\  {} AD\bot AC \\ \end{array} \right.\Rightarrow AD\bot (ABC)\Rightarrow AD\bot BC$

Mặt khác $AH\bot BC\Rightarrow BC\bot (ADH)\Rightarrow BC\bot DH$

Tương tự chứng minh trên ta có: $BH\bot CD$

Do đó H là trực tâm của tam giác BCD.

b) Gọi $E=DH\cap BC$, do $BC\bot (ADH)\Rightarrow BC\bot AE$

Xét ∆ ABC vuông tại A có đường cao AE ta có: $\frac{1}{A{{E}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{C}^{2}}}$

Lại có: $\frac{1}{A{{H}^{2}}}=\frac{1}{A{{D}^{2}}}+\frac{1}{A{{E}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{C}^{2}}}+\frac{1}{A{{D}^{2}}}$(đpcm).

c) Đặt AB = x; AC = y; AD = z. Ta có: $\left\{ \begin{array}  {} BC=\sqrt{{{x}^{2}}+{{y}^{2}}} \\  {} BD=\sqrt{{{x}^{2}}+{{z}^{2}}} \\  {} CD=\sqrt{{{y}^{2}}+{{z}^{2}}} \\ \end{array} \right.$

Khi đó $\text{cosB=}\frac{B{{C}^{2}}+B{{D}^{2}}-C{{D}^{2}}}{2.BC.BD}=\frac{{{x}^{2}}}{BC.BD}>0\Rightarrow \widehat{CBD}<{{90}^{\circ }}$

Tương tự chứng minh trên ta cũng có $\left\{ \begin{array}  {} \widehat{BDC}<{{90}^{\circ }} \\  {} \widehat{BCD}<{{90}^{\circ }} \\ \end{array} \right.\Rightarrow$ tam giác BCD có 3 góc nhọn.

Lời giải chi tiết

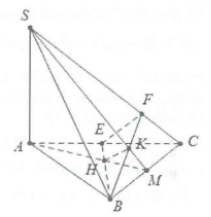
a) Giả sử $AH\bot BC$ tại M.

Ta có: $\left\{ \begin{array}  {} BC\bot AM \\  {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAM)\Rightarrow BC\bot SM$

Mặt khác $SK\bot BC\Rightarrow$ S, K, M thẳng hàng do đó AH, SK, BC đồng quy tại điểm M.

b) Do H là trực tâm của tam giác ABC nên $BH\bot AC$

Mặt khác $BH\bot SA\Rightarrow BH\bot (SAC)\Rightarrow BH\bot SC$

Lại có: $BK\bot SC\Rightarrow SC\bot (BHK)$

c) Do $SC\bot (BHK)\Rightarrow SC\bot HK$, mặt khác $BC\bot (SAM)\Rightarrow BC\bot HK$

Do đó $HK\bot (SBC)$

Lời giải chi tiết

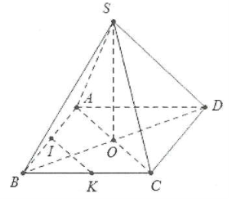
a) Do SA = SC $\Rightarrow$ ∆ SAC cân tại S có trung tuyến SO đồng thời là đường cao suy ra $SO\bot AC$

Tương tự ta có: $SO\bot BD\Rightarrow SO\bot (ABCD)$

b) Do ABCD là hình thoi nên $AC\bot BD$

Mặt khác $SO\bot (ABCD)\Rightarrow AC\bot SO$

Do vậy $AC\bot (SBD)$

IK là đường trung bình trong tam giác BAC nên $IK//AC$ mà $AC\bot (SBD)\Rightarrow IK\bot (SBD)$

Lời giải chi tiết

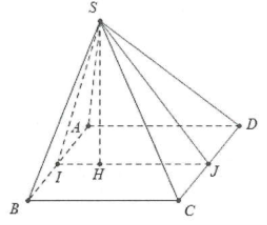
a) Ta có: ∆SAB đều cạnh a nên $SI=\frac{a\sqrt{3}}{2}$

Tứ giác IBCJ là hình chữ nhật nên IJ = BC = a

∆SCD là tam giác vuông cân đỉnh S $\Rightarrow SJ=\frac{CD}{2}=\frac{a}{2}$

Do đó $S{{J}^{2}}+S{{I}^{2}}=I{{J}^{2}}={{a}^{2}}\Rightarrow \vartriangle SIJ$ vuông tại S.

b) Do ∆SCD cân tại S nên $SJ\bot CD$

Do $AB//CD\Rightarrow SJ\bot AB$

Mặt khác $SJ\bot SI\Rightarrow SJ\bot (SAB)$

Chứng minh tương tự ta có: $SI\bot (SCD).$

c) Do $SI\bot (SCD)\Rightarrow SI\bot CD$

Mặt khác $CD\bot IJ\Rightarrow CD\bot (SIJ)\Rightarrow CD\bot SH$

Do $SH\bot IJ\Rightarrow SH\bot (ABCD)$

Lời giải chi tiết

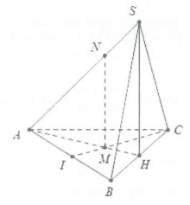
Do điểm M thuộc đường trung tuyến CI và MC = 2MI

$\Rightarrow$ M là trọng tâm tam giác ABC $\Rightarrow M=AH\cap CI$

Ta có : $\frac{NA}{NS}=\frac{MA}{MH}=2\Rightarrow MN//SH$

Mặt khác $SH\bot (ABC)\Rightarrow MN\bot (ABC)$