Bài toán mặt cầu với chóp có cạnh bên vuông góc đáy – cách giải và bài tập có đáp án chi tiết

Bài toán mặt cầu với chóp có cạnh bên vuông góc đáy – cách giải và bài tập có đáp án

Phương pháp, định hướng giải

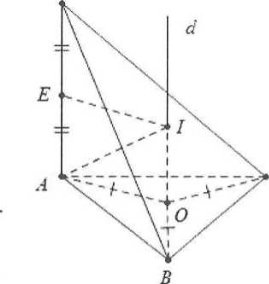
Xét khối chóp $S.ABC$ có $SA\bot \left( ABC \right)$. Tìm tâm và tính bán kính mặt cầu ngoại tiếp khối chóp $S.ABC$.

Dựng tâm. Dựng trục đường tròn ngoại tiếp d của tam giác $ABC$, thì $d//SA$

Trong mặt phẳng $\left( SA;d \right)$, dựng đường trung trực $\Delta$ của SA. Tâm I của mặt cầu là giao điểm của d và $\Delta$.

Tính bán kính $R$ của mặt cầu

Gọi O là tâm đường tròn ngoại tiếp $\Delta ABC$.

Gọi E là trung điểm của SA.

Xét $\Delta AOI$ vuông tại O

Ta có ${{R}^{2}}=A{{I}^{2}}=O{{A}^{2}}+O{{I}^{2}}=O{{A}^{2}}+A{{E}^{2}}=O{{B}^{2}}+{{\left( \frac{SA}{2} \right)}^{2}}.$

với $OA={{R}_{d}}$ là bán kính đường tròn ngoại tiếp đáy.

Khi đó: ${{R}_{S.ABC}}=\sqrt{\frac{S{{A}^{2}}}{4}+R_{d}^{2}}.$

Tổng quát: Cho khối chóp $S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ có $SA\bot A{{A}_{1}}{{A}_{2}}.$ Gọi ${{R}_{d}}$ là bán kính đường tròn ngoại tiếp đa giác $A{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ thì bán kính mặt cầu ngoại tiếp R của khối chóp $S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ được tính theo công thức: $R=\sqrt{\frac{S{{A}^{2}}}{4}+R_{d}^{2}}.$

Bài tập trắc nghiệm mặt cầu, khối cầu có đáp án chi tiết

Lời giải chi tiết

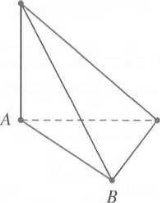
+ Ta có $\widehat{SB;\left( ABC \right)}=\widehat{SBA}={{60}^{0}}\Rightarrow SA=\tan {{60}^{0}}.AB=a\sqrt{3}.$

Tam giác ABC vuông tại $A\Rightarrow A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\Rightarrow BC=2a$.

+ Hình chóp $S.ABC$ có chiều cao $h=a\sqrt{3};$ bán kính ${{R}_{day}}=\frac{BC}{2}=a$

$\Rightarrow$ Bán kính mặt cầu cần tính là $R=\sqrt{{{a}^{2}}+\frac{{{\left( a\sqrt{3} \right)}^{2}}}{4}}=\frac{a\sqrt{7}}{2}.$

Chọn D.

Lời giải chi tiết

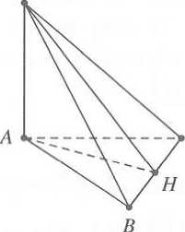
+ Đặt $AB=x\xrightarrow{{}}{{S}_{\Delta ABC}}=\frac{{{x}^{2}}\sqrt{3}}{4}={{a}^{2}}\sqrt{3}\Rightarrow x=2a.$

Gọi H là trung điểm của $BC\Rightarrow AH\bot BC$ mà $SA\bot BC$

Suy ra $BC\bot \left( SAH \right)\Rightarrow BC\bot SH\Rightarrow {{S}_{\Delta SBC}}=\frac{1}{2}SH.BC=2{{a}^{2}}$

$\Rightarrow \frac{1}{2}SH.2a=2{{a}^{2}}\Rightarrow SH=2a\Rightarrow SA=\sqrt{S{{H}^{2}}-A{{H}^{2}}}=a.$

+ Hình chóp $S.ABC$ có chiều cao $h=SA=a;$ bán kính ${{R}_{day}}=\frac{2a\sqrt{3}}{3}$

$\Rightarrow$ Bán kính mặt cầu cần tính là $R=\sqrt{\frac{{{\left( 2a\sqrt{3} \right)}^{2}}}{3}+\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{57}}{6}.$

Chọn A.

Lời giải chi tiết

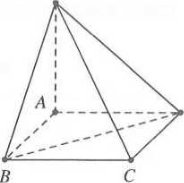
+  Đặt $AB=x\xrightarrow{{}}BD=x\sqrt{2}$ và $SB=\sqrt{S{{A}^{2}}+A{{B}^{2}}}=\sqrt{{{x}^{2}}+2{{a}^{2}}}$

Tam giác SBD đều $\Rightarrow SB=BD\xrightarrow{x\sqrt{2}=\sqrt{{{x}^{2}}+2{{a}^{2}}}}x=a\sqrt{2}$

+ Hình chóp $S.ABCD$ có chiều cao $h=a\sqrt{2};$ bán kính ${{R}_{day}}=a$

$\Rightarrow$ Bán kính mặt cầu cần tính là $R=\sqrt{{{a}^{2}}+\frac{{{\left( a\sqrt{2} \right)}^{2}}}{4}}=\frac{a\sqrt{6}}{2}.$

Vậy thể tích khối cầu là $V=\frac{4\pi }{3}.{{\left( \frac{a\sqrt{6}}{2} \right)}^{3}}=\sqrt{6}{{a}^{3}}.$ Chọn C.

Lời giải chi tiết

Ta có $\left\{ \begin{matrix}   SA\bot BC  \\   AB\bot BC  \\\end{matrix}\Rightarrow CB\bot \left( SAB \right)\Rightarrow \left( \widehat{SC;\left( SAB \right)} \right) \right.=\left( \widehat{SC;SB} \right)=\widehat{CSB}$

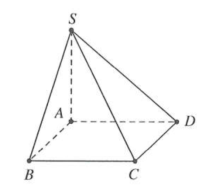
Tam giác SBC vuông tại $B\Rightarrow \tan \widehat{CSB}=\frac{BC}{SB}\Rightarrow SB=a\sqrt{3}$

Tam giác SAB vuông tại $A\Rightarrow SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=a\sqrt{2}$

Vậy $h=SA=a\sqrt{2};{{R}_{d}}=\frac{BD}{2}=\frac{AB\sqrt{2}}{2}=\frac{a\sqrt{2}}{2}$ nên $R=a.$

Chọn A.

Lời giải chi tiết

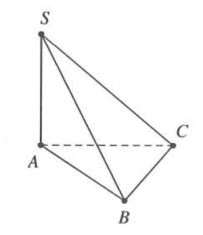
Ta có $SA\bot \left( ABC \right)\Rightarrow \left( \widehat{SB;(ABC)} \right)=\left( \widehat{SB;AB} \right)=\overset\frown{SBA}={{45}^{0}}.$

Tam giác SAB vuông tại $A$, có $\widehat{SBA}={{45}^{0}}\Rightarrow SA=AB=a$.

Tam giác ABC vuông tại $A$, có $\sin \widehat{ACB}=\frac{AB}{AC}\Rightarrow AC=2a.$

Suy ra bán kính đường tròn ngoại tiếp $\Delta ABC$ là ${{R}_{\Delta ABC}}=\frac{AC}{2}=a.$

Vậy bán kính mặt cầu cần tính là

$R=\sqrt{R_{\Delta ABC}^{2}+\frac{S{{A}^{2}}}{4}}=\sqrt{{{a}^{2}}+\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{5}}{2}.$ Chọn B.

Lời giải chi tiết

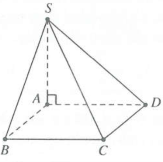
Vì $CD\bot \left( SAD \right)\Rightarrow \left( \widehat{\left( SCD \right);\left( ABCD \right)} \right)=\left( \widehat{SD;AD} \right)=\overset\frown{SDA}={{45}^{0}}.$

Tam giác SAD vuông tại A, có $\widehat{SDA}={{45}^{0}}\Rightarrow SA=AD=x.$

Bán kính đường tròn ngoại tiếp ABCD là ${{R}_{ABCD}}=\frac{AC}{2}=\frac{x\sqrt{2}}{2}.$

Bán kính mặt cầu là $R=\sqrt{R_{ABCD}^{2}+\frac{S{{A}^{2}}}{4}}=\frac{x\sqrt{3}}{2}.$

Mà $R_{S.ABCD}^{{}}=\frac{a\sqrt{6}}{2}\Rightarrow \frac{x\sqrt{3}}{2}=\frac{a\sqrt{6}}{2}\Leftrightarrow x=a\sqrt{2}.$

Vậy ${{S}_{\Delta SAB}}=\frac{{{x}^{2}}}{2}={{a}^{2}}.$ Chọn C.

Lời giải chi tiết

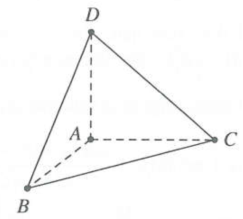
Vì $A,B,C,D$ thuộc $\left( S \right)\Rightarrow \left( S \right)$ ngoại tiếp tứ diện ABCD.

Tứ diện ABCD có chiều cao $h=AD;$ đáy là tam giác ABC.

Đặt $AB=a,AC=b,AD=c\Rightarrow h=c$ và ${{R}_{day}}=\frac{BC}{2}=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{2}$

$\Rightarrow$ Bán kính mặt cầu ngoại tiếp tứ diện ABCD là

$R=\sqrt{{{\left( \frac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{2} \right)}^{2}}+\frac{{{c}^{2}}}{4}}=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}{2}=\sqrt{3}\Rightarrow {{a}^{2}}+{{b}^{2}}+{{c}^{2}}=12$

Ta có $12={{a}^{2}}+{{b}^{2}}+{{c}^{2}}\ge 3\sqrt[3]{{{\left( abc \right)}^{2}}}\Leftrightarrow abc\le 8\xrightarrow{{}}{{V}_{ABCD}}=\frac{abc}{6}\le \frac{4}{3}.$ Chọn C.

Lời giải chi tiết

Vì $SA=SB=SD$ và $\Delta ABD$ đều cạnh $a\xrightarrow[{}]{}S.ABD$ là hình chóp tam giác đều.

Mặt khác $\widehat{BSD}={{90}^{0}}\Rightarrow SB\bot SD\Rightarrow SA,SB,SD$ đôi một vuông góc và bằng $\frac{a\sqrt{2}}{2}.$

Áp dụng công thức giải nhanh, ta được ${{R}_{S.ABD}}=\frac{\sqrt{S{{A}^{2}}+S{{B}^{2}}+S{{D}^{2}}}}{2}=R=\frac{a\sqrt{6}}{4}.$ Chọn A.

Lời giải chi tiết

Đặt $OA=a,OB=b$ với $a,b>0$ suy ra $OA+OB=OC\Leftrightarrow a+b=1.$

Bán kính mặt cầu ngoại tiếp tứ diện OACB ($OA,OB,OC$ đôi một vuông góc) là

$R=\frac{\sqrt{O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}}}{2}=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}+1}}{2}=\frac{1}{2}\sqrt{{{a}^{2}}+{{\left( 1-a \right)}^{2}}+1}=\frac{1}{2}\sqrt{2{{a}^{2}}-2a+2}$

Dễ thấy ${{a}^{2}}-a+1={{\left( a-\frac{1}{2} \right)}^{2}}+\frac{3}{4}\ge \frac{3}{4}\Rightarrow \sqrt{{{a}^{2}}-a+1}\ge \frac{\sqrt{3}}{2}\Rightarrow R\ge \frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{4}.$

Dấu bằng xảy ra khi và chỉ khi $a=b=\frac{1}{2}.$ Vậy giá trị bé nhất cần tìm là $\frac{\sqrt{6}}{4}.$ Chọn A.

Lời giải chi tiết

Dễ thấy tâm mặt cầu ngoại tiếp tứ diện $AB'C'C$ cũng là tâm mặt cầu ngoại tiếp khối lăng trụ $ABC.A'B'C'$ hay là tâm mặt cầu ngoại tiếp khối chóp $A'.ABC.$

Sử dụng công thức tính nhanh, ta được $R=\sqrt{{{r}^{2}}+\frac{{{h}^{2}}}{4}}=\sqrt{{{\left( {{R}_{\Delta ABC}} \right)}^{2}}+\frac{A'{{A}^{2}}}{4}}.$

Ta có $\cos \widehat{BAC}=\frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2.AB.AC}=\frac{{{a}^{2}}+{{a}^{2}}-3{{a}^{2}}}{2{{a}^{2}}}=-\frac{1}{2}\Rightarrow \widehat{BAC}={{120}^{0}}.$

$\Rightarrow {{R}_{\Delta ABC}}=\frac{BC}{2\sin \widehat{BAC}}=\frac{a\sqrt{3}}{2.\sin {{120}^{0}}}=a.$ Khi đó $R=\sqrt{{{\left( {{R}_{\Delta ABC}} \right)}^{2}}+\frac{A'{{A}^{2}}}{4}}=a\sqrt{2}.$ Chọn D.

Lời giải chi tiết

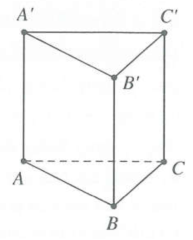
Ta có $\left\{ \begin{matrix}   AA'\bot BC  \\   AB\bot BC  \\\end{matrix} \right.\Rightarrow BC\bot \left( AA'B'B \right)$ và $\left\{ \begin{matrix}   \left( A'BC \right)\cap \left( AA'B'B \right)=A'B  \\   \left( ABC \right)\cap \left( AA'B'B \right)=AB\text{   }  \\\end{matrix} \right.$

$\Rightarrow \widehat{\left( A'BC \right);\left( ABC \right)}=\left( \widehat{A'B;AB} \right)=\widehat{A'BA}={{60}^{0}}\Rightarrow AA'=AB.\tan {{60}^{0}}=a\sqrt{3}$

Tam giác ABC vuông cân tại $B,$ có ${{R}_{\Delta ABC}}=\frac{AC}{2}=\frac{a\sqrt{2}}{2}.$

Suy ra bán kính mặt cầu là $R=\sqrt{R_{_{\Delta ABC}}^{2}+\frac{A'{{A}^{2}}}{4}}=\frac{a\sqrt{5}}{2}.$

Vậy thể tích khối cầu cần tính là $V=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi .{{\left( \frac{a\sqrt{5}}{2} \right)}^{3}}=\frac{5\sqrt{5}\pi {{a}^{3}}}{6}.$ Chọn B.

Lời giải chi tiết

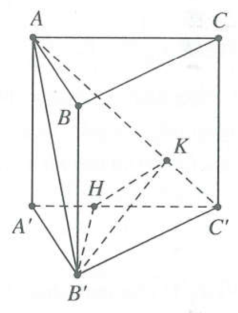
Kẻ $B'H\bot A'C'\left( H\in A'C' \right),$ kẻ $HK\bot AC'\left( K\in AC' \right)$.

Ta có $B'H\bot \left( ACC' \right)\Rightarrow \left\{ \begin{matrix}   B'H\bot AC'  \\   HK\bot AC'  \\\end{matrix}\Rightarrow AC'\bot \left( B'HK \right) \right.$

Khi đó $\widehat{\left( ACC' \right);\left( AB'C' \right)}=\widehat{\left( HK;B'K \right)}=\widehat{B'KH}={{60}^{0}}.$

Tam giác $A'B'C'$ vuông cân tại $B'\Rightarrow B'H=\frac{A'C'}{2}=\frac{a\sqrt{2}}{2}.$

Tam giác $B'HK$ vuông tại H, có $\sin \widehat{B'HK}=\frac{BH}{B'K}\Rightarrow B'K=\frac{a\sqrt{6}}{3}.$

Tam giác $AB'C'$ vuông tại $B',$ có $B'K$ là đường cao

$\Rightarrow \frac{1}{B'{{K}^{2}}}=\frac{1}{AB{{'}^{2}}}+\frac{1}{B'C{{'}^{2}}}\Rightarrow \frac{1}{AB{{'}^{2}}}=\frac{1}{2{{a}^{2}}}\Rightarrow AB'=a\sqrt{2}.$

Tam giác $AA'B$ vuông tại $A',$ có $AA'=\sqrt{AB{{'}^{2}}-A'B{{'}^{2}}}=\sqrt{{{\left( a\sqrt{2} \right)}^{2}}-{{a}^{2}}}=a$.

Vậy bán kính mặt cầu cần tìm là $R=\sqrt{R_{_{\Delta ABC}}^{2}+\frac{AA{{'}^{2}}}{4}}=\sqrt{{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}+\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{3}}{2}.$ Chọn C.