Bài toán mặt cầu, khối cầu và Hình chóp bất kì (bài toán Tổng quát – Nâng cao)

Bài toán mặt cầu, khối cầu và Hình chóp bất kì (bài toán Tổng quát – Nâng cao)

Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là

 $R=\sqrt{{{x}^{2}}+{{r}^{2}}}$ với

r là bán kính đường tròn ngoại tiếp đa giác đáy.

$x=\frac{S{{O}^{2}}-{{r}^{2}}}{2h}:S$ là đỉnh hình chóp, O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao khối chóp.

Bài tập trắc nghiệm mặt cầu, khối cầu và hình chóp bất kì có đáp án chi tiết

Lời giải chi tiết

Hình vẽ tham khảo

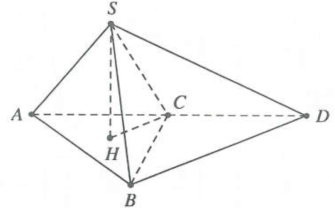
Vì C là tâm đường tròn ngoại tiếp $\Delta ABD$ nên $r=BC=a$

Gọi H là hình chiếu của S trên mặt phẳng $\left( ABC \right)\Rightarrow H$ là tâm đường tròn ngoại tiếp $\Delta ABC$

Tam giác SHC vuông tại H, có $SC=\frac{2a\sqrt{3}}{3};HC=\frac{a\sqrt{3}}{3}\Rightarrow SH=\sqrt{S{{C}^{2}}-H{{C}^{2}}}=a$

Vậy $r=h=a$ và $SC=\frac{2a\sqrt{3}}{3}$ nên $R=\frac{a\sqrt{37}}{6}.$ Chọn A.

Lời giải chi tiết

Vì E là trung điểm $DC\Rightarrow \Delta EBC$ vuông tại E

Gọi M là trung điểm của BC

$\Rightarrow M$ là tâm đường tròn ngoại tiếp tam giác EBC

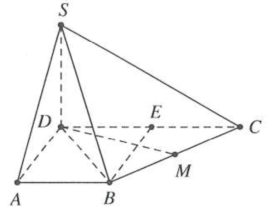
Xét hình chóp $S.BCE$ có S là đỉnh, M là tâm đáy, chiều cao $h=SD$ và bán kính đường tròn ngoại tiếp đáy $r=\frac{BC}{2}=\frac{a\sqrt{2}}{2}$

$\Delta BCD$ vuông cân tại $B\Rightarrow DM=\sqrt{B{{D}^{2}}+B{{M}^{2}}}=\frac{a\sqrt{10}}{2}$

$\Delta SDM$ vuông tại $D\Rightarrow SM=\sqrt{S{{D}^{2}}+D{{M}^{2}}}=\frac{a\sqrt{14}}{2}$

Áp dụng công thức, ta được $R=\sqrt{{{\left( \frac{S{{M}^{2}}-{{r}^{2}}}{2.SD} \right)}^{2}}+{{r}^{2}}}=\frac{a\sqrt{11}}{2}.$ Chọn D.

Lời giải chi tiết

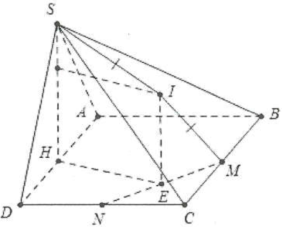
Gọi H là trung điểm của $AD\Rightarrow SH\bot AD$

$\Rightarrow SH\bot \left( ABCD \right).$ Gọi E là trung điểm của MN, dựng đường thẳng d qua E song song với SH, trên d lấy điểm I sao cho $IS=IC\Rightarrow I$ là tâm mặt cầu ngoại tiếp khối chóp $S.CMN\Rightarrow IS=IC=IM=IN=R.$

Ta có: $CE=\frac{MN}{2}=\frac{a\sqrt{2}}{4}\Rightarrow IE=\sqrt{{{R}^{2}}-\frac{{{a}^{2}}}{8}};SH=\frac{a\sqrt{3}}{2}$

$H{{E}^{2}}={{\left( \frac{3}{4}CD \right)}^{2}}+{{\left( \frac{1}{4}AD \right)}^{2}}=\frac{5{{a}^{2}}}{8}$

Lại có ${{R}^{2}}-H{{E}^{2}}={{\left( SH-IE \right)}^{2}}\Leftrightarrow {{R}^{2}}-\frac{5{{a}^{2}}}{8}={{\left( \frac{a\sqrt{3}}{2}-\sqrt{{{R}^{2}}-\frac{{{a}^{2}}}{8}} \right)}^{2}}\Rightarrow R=\frac{a\sqrt{93}}{12}.$ Chọn D.

Lời giải chi tiết

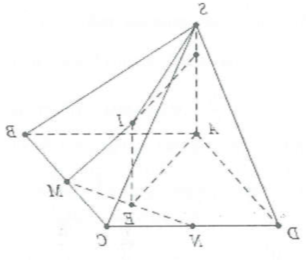
Gọi E là trung điểm của MN, dựng đường thẳng d qua E song song với SA, trên d lấy điểm I sao cho $IS=IC\Rightarrow I$  là tâm mặt cầu ngoại tiếp khối chóp$S.CMN\Rightarrow IS=IC=IM=IN=R.$

Ta có: $CE=\frac{MN}{2}=\frac{a\sqrt{2}}{4}\Rightarrow IE=\sqrt{{{R}^{2}}-\frac{{{a}^{2}}}{8}};SA=2a$

$A{{E}^{2}}={{\left( \frac{3}{4}CD \right)}^{2}}+{{\left( \frac{3}{4}AD \right)}^{2}}=\frac{9{{a}^{2}}}{8}$

Lại có ${{R}^{2}}-A{{E}^{2}}={{\left( SA-IE \right)}^{2}}$

$\Leftrightarrow {{R}^{2}}-\frac{9{{a}^{2}}}{8}={{\left( 2a-\sqrt{{{R}^{2}}-\frac{{{a}^{2}}}{8}} \right)}^{2}}\Rightarrow R=\frac{3a\sqrt{3}}{4}.$

Chọn C.

Lời giải chi tiết

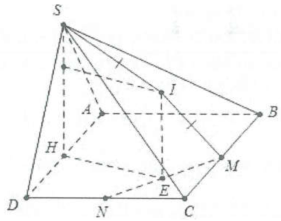
Gọi H là trung điểm của $AD\Rightarrow SH\bot AD$

$\Rightarrow SH\bot \left( ABCD \right)$. Gọi E là trung điểm của MN, dựng đường thẳng d qua E song song với SH, trên d lấy điểm I sao cho $IS=IC\Rightarrow I$  là tâm mặt cầu ngoại tiếp khối chóp$S.CMN\Rightarrow IS=IC=IM=IN=R.$

Ta có: $CE=\frac{MN}{2}=\frac{a\sqrt{5}}{4}\Rightarrow IE=\sqrt{{{R}^{2}}-\frac{5{{a}^{2}}}{16}};SH=a\sqrt{3}$

$H{{E}^{2}}={{\left( \frac{3}{4}CD \right)}^{2}}+{{\left( \frac{1}{4}AD \right)}^{2}}=\frac{13{{a}^{2}}}{16}$

Lại có ${{R}^{2}}-H{{E}^{2}}={{\left( SH-IE \right)}^{2}}$ $\Leftrightarrow {{R}^{2}}-\frac{13{{a}^{2}}}{16}={{\left( a\sqrt{3}-\sqrt{{{R}^{2}}-\frac{5{{a}^{2}}}{16}} \right)}^{2}}\Rightarrow R=\frac{2a\sqrt{3}}{3}.$

Chọn A.

Lời giải chi tiết

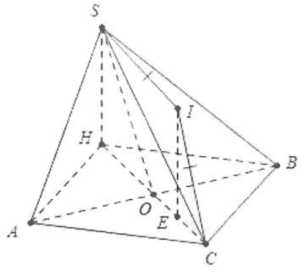
Gọi H là đối xứng của C qua$AB\Rightarrow CH\bot AB.$

O là trung điểm của $CH$

$\Rightarrow OH=CO=\frac{a\sqrt{3}}{2};\widehat{SOH}={{60}^{0}}$

Suy ra $SH=OH\tan {{60}^{0}}=\frac{3a}{2}$

Gọi E là trọng tâm tam giác ABC, dựng đường thẳng d qua E song song với SH, trên d lấy điểm I sao cho $IS=IC\Rightarrow I$  là tâm mặt cầu ngoại tiếp khối chóp$S.CMN$

$\Rightarrow IS=IC=IM=IN=R.$

có: $CE=\frac{2CO}{3}=\frac{a\sqrt{3}}{3}\Rightarrow IE=\sqrt{{{R}^{2}}-\frac{{{a}^{3}}}{3}};HE=2CE=\frac{2a\sqrt{3}}{3}$z

Lại có ${{R}^{2}}-H{{E}^{2}}={{\left( SH-IE \right)}^{2}}$ $\Leftrightarrow {{R}^{2}}-\frac{4{{a}^{2}}}{3}={{\left( \frac{3a}{2}-\sqrt{{{R}^{2}}-\frac{{{a}^{2}}}{3}} \right)}^{2}}\Rightarrow R=\frac{a\sqrt{217}}{12}.$

Chọn B.