Bài tập về tính thiết diện qua đỉnh nón có đáp án chi tiết

Bài tập về tính thiết diện qua đỉnh nón có đáp án chi tiết

Dưới đây là một số bài tập trắc nghiệm liên quan đến thiết diện của hình nón hay ra trong đề thi đại học có đáp án chi tiết

Lời giải chi tiết

Thiệt diện qua trục hình nón là tam giác cân SAB có cạnh bên SA = l, cạnh đáy AB = 2R

Theo bài ra, ta có $S{{A}^{2}}+S{{B}^{2}}=A{{B}^{2}}\Leftrightarrow 2{{l}^{2}}=4{{R}^{2}}\Leftrightarrow l=R\sqrt{2}$

Mặt khác $AB=2R=a\sqrt{6}\Rightarrow R=a\sqrt{6}$suy ra $l=\frac{a\sqrt{6}}{2}.\sqrt{2}=a\sqrt{3}$

Do đó $h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\frac{a\sqrt{6}}{2}\to V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi {{a}^{3}}\sqrt{6}}{4}$

Chọn A.

Lời giải chi tiết

Thiết diện qua trục hình nón là tam giác cân SAB có cạnh bên SA = l, cạnh đáy AB =2R

Theo bài ra, tam giác SAB vuông $\Rightarrow SA\bot SB\Rightarrow {{S}_{\Delta SAB}}=\frac{S{{A}^{2}}}{2}=\frac{{{l}^{2}}}{2}={{a}^{2}}\Rightarrow l=a\sqrt{2}$

Do đó $l=R\sqrt{2}\Rightarrow R=\frac{l}{\sqrt{2}}=a$. Vậy diện tích cần tìm là ${{S}_{xq}}=\pi Rl=\sqrt{2}\pi {{a}^{2}}$. Chọn B.

Lời giải chi tiết

Theo bài ra, tam giác SAB đều cạnh a $\Rightarrow SA=SB=AB=a$

Do đó, chiều cao $SO=\frac{a\sqrt{3}}{2}$, bán kính đáy $R=\frac{AB}{2}=\frac{a}{2}$

Vậy thể tích cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}.{{\left( \frac{a}{2} \right)}^{2}}.\frac{a\sqrt{3}}{2}=\frac{\pi {{a}^{3}}\sqrt{3}}{24}$

Chọn C

Lời giải chi tiết

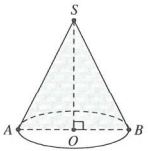
Theo bài ra, tacó $AB=2R=18$ và $\widehat{SAO}={{30}^{o}}$

Tam giác SAO vuông tại O, có $SO=OA.\tan \widehat{SAO}=9.\tan {{30}^{o}}=3\sqrt{3}$

Thiết diện qua trục hình nón là tam giác cân SAB

Suy ra diện tích cần tính là ${{S}_{\Delta SAB}}=\frac{1}{2}SO.AB=\frac{1}{2}.3\sqrt{3}.18=27\sqrt{3}c{{m}^{2}}$

Chọn D

Lời giải chi tiết

 Theo bài ra, ta có $\left\{ \begin{array}  {} 2l+2R=10 \\  {} \frac{1}{2}h.2R=2\sqrt{5} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} l+R=5 \\  {} h.R=2\sqrt{5} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} l=5-R \\  {} R.\sqrt{{{l}^{2}}-{{R}^{2}}}=2\sqrt{5} \\ \end{array} \right.$

Do đó ${{R}^{2}}.\left[ \left( 5-{{R}^{2}} \right)-{{R}^{2}} \right]=20\Leftrightarrow {{R}^{2}}\left( 25-10R \right)=5\Leftrightarrow 10{{R}^{3}}-25{{R}^{2}}+20=0\Rightarrow R=2$

Suy ra $h=\sqrt{5}$ Vậy thể tích cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{.2}^{2}}.\sqrt{5}=\frac{4\sqrt{5}\pi }{3}c{{m}^{3}}$. Chọn B

Lời giải chi tiết

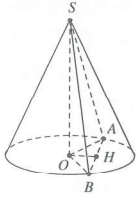
Vì góc ở đỉnh bằng ${{120}^{o}}\Rightarrow 2R=l\sqrt{3}\Rightarrow SA=\frac{2\sqrt{3}}{3}OA=\frac{2\sqrt{3}}{3}R$

Gọi H là trung điểm của AB$\Rightarrow OH\bot AB$ mà $SO\bot OH$

Suy ra OH là đoạn vuông góc chung của AB và SO => OH =3

Tam giác OAH vuông tại H, có $AH=\sqrt{O{{A}^{2}}-O{{H}^{2}}}=\sqrt{{{R}^{2}}-9}$

Tam giác SAB vuông tại S, có $S{{A}^{2}}+S{{B}^{2}}=A{{B}^{2}}$

$\Leftrightarrow 2.{{\left( \frac{2\sqrt{3}}{3}R \right)}^{2}}=4\left( {{R}^{2}}-9 \right)\Leftrightarrow -\frac{4}{3}{{R}^{2}}=-36\Rightarrow R=3\sqrt{3}\Rightarrow l=6$

Vậy diện tích xung quanh cần tính là ${{S}_{xq}}=\pi Rl=18\sqrt{3}\pi$.

Chọn A. 

Lời giải chi tiết

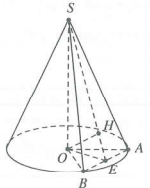
Theo giả thiết, ta có tam giác OAB đều cạnh R

Gọi E là trung điểm AB, suy ra $OE\bot AB$và $OE=\frac{R\sqrt{3}}{2}$

Gọi h là hình chiếu của O trên SE $\Rightarrow OH\bot SE$

Ta có $\left\{ \begin{array}  {} AB\bot OE \\  {} AB\bot SO \\ \end{array} \right.\Rightarrow AB\bot \left( SEO \right)\Rightarrow AB\bot OH$

Từ đó suy ra $OH\bot \left( SAB \right)$ nên $d\left( O;\left( SAB \right) \right)=OH=\frac{R}{2}$

Tam giác SEO vuông tại O, có $\frac{1}{S{{O}^{2}}}=\frac{1}{O{{H}^{2}}}-\frac{1}{O{{E}^{2}}}=\frac{8}{3{{R}^{2}}}\Rightarrow SO=\frac{R\sqrt{6}}{4}$

Chọn B

Lời giải chi tiết

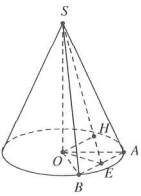
Theo giả thiết, ta có tam giác SAB vuông cân tại S

Gọi E là trung điểm AB, suy ra $\left\{ \begin{array}  {} SE\bot AB \\  {} OE\bot AB \\ \end{array} \right.$ và $SE=\frac{1}{2}AB$

Ta có ${{S}_{\Delta SAB}}=\frac{1}{2}AB.SE=4{{a}^{2}}\Leftrightarrow \frac{1}{2}AB.\frac{1}{2}AB=4{{a}^{2}}\Rightarrow AB=4a$

Gọi H là hình chiếu của O trên SE => $OH\bot SE$

Lại có $\left\{ \begin{array}  {} AB\bot OE \\  {} AB\bot SO \\ \end{array} \right.\Rightarrow AB\bot \left( SEO \right)\Rightarrow AB\bot OH$

Từ đó suy ra $OH\bot \left( SAB \right)\Rightarrow \widehat{\left( SO;\left( SAB \right) \right)}=\widehat{OSH}={{30}^{o}}$

Tam giác SEO vuông tại O, có $SO=SE.\cos \widehat{\text{OS}E}=a\sqrt{3}$.

Chọn D.

Lời giải chi tiết

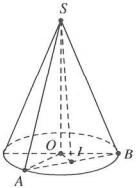
Gọi I là trung điểm AB, suy ra $OI\bot AB,SI\bot AB$ và OI = a

Tam giác SAO vuông tại O, có $OA=SA.\cos \widehat{SAO}=\frac{SA\sqrt{3}}{2}$

Tam giác SAI vuông tại I, có $IA=SA\cos \widehat{SAB}=\frac{SA}{2}$

Tam giác OIA vuông tại I, có $O{{A}^{2}}=O{{I}^{2}}+I{{A}^{2}}$

$\Leftrightarrow \frac{3}{4}S{{A}^{2}}={{a}^{2}}+\frac{1}{4}S{{A}^{2}}\Leftrightarrow S{{A}^{2}}=2{{a}^{2}}\Rightarrow SA=a\sqrt{2}$

Vậy độ dài đường sinh cần tìm là $l=a\sqrt{2}$. Chọn C.

Lời giải chi tiết

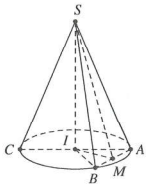
Vì góc ở đỉnh là 60^o nên thiết diện qua trục SAC là tam giác đều cạnh 2R $\Rightarrow$ Đường cao của hình nón là $SI=R\sqrt{3}$
Tam giác SA là thiết diện qua đỉnh, chắn trên đáy cung AB có số đo bằng 90° nên IAB là tam giác vuông cân tại I $\Rightarrow AB=R\sqrt{2}$

Gọi M là trung điểm của AB thì $\left\{ \begin{array}  {} IM\bot AB \\  {} SM\bot AB \\ \end{array} \right.$và $IM=\frac{R\sqrt{2}}{2}$

Tam giác SMI vuông tại I, có $SM=\sqrt{S{{I}^{2}}+I{{M}^{2}}}=\frac{R\sqrt{14}}{2}$

Vậy diện tích cần tính là ${{S}_{\Delta SAB}}=\frac{1}{2}AB.SM=\frac{{{R}^{2}}\sqrt{7}}{2}$ . Chọn A.