Bài tập về tính thiết diện hình trụ có đáp án chi tiết

Bài tập về tính thiết diện hình trụ có đáp án chi tiết

Dưới đây là bài tập trắc nghiệm tính thiết diện hình trụ hay ra trong đề thi có đáp án chi tiết

Lời giải chi tiết

Thiết diện qua trục hình trụ là hình chữ nhật có hai kích thước h và 2R

Theo bài ra, ta có $h=2R=2a\Rightarrow \left\{ \begin{array}  {} R=a \\  {} h=2\text{a} \\ \end{array} \right..$ Vậy ${{S}_{xq}}=2\pi Rh=2\pi .a.2\text{a}=4\pi {{a}^{2}}.$ Chọn B.

Lời giải chi tiết

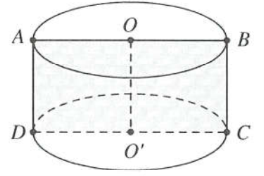
Thiết diện qua trục của hình trụ là hình chữ nhật ABCD có hai kích thước $AB=2R,AD=h$

Theo bài ra, ta có ABCD là hình vuông $\Rightarrow AB=AD\Leftrightarrow h=2R$

Diện tích toàn phần của hình trụ là ${{S}_{tp}}=2\pi Rh+2\pi {{R}^{2}}$

$=2\pi R.2R+2\pi {{R}^{2}}=6\pi {{R}^{2}}=6\pi \xrightarrow{{}}R=1\Rightarrow h=2.$

Vậy thề tích khối trụ là $V=\pi {{R}^{2}}h=2\pi .$ Chọn A.

Lời giải chi tiết

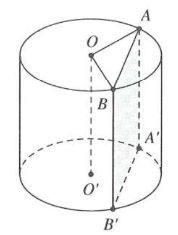
Thiết diện qua trục hình trụ là hình chữ nhật có hai kích thước h, 2R

Theo bài ra, ta có $\left\{ \begin{array}  {} h=2\text{R} \\  {} {{S}_{xq}}=4\pi  \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} h=2\text{R} \\  {} 2\pi Rh=4\pi  \\ \end{array} \right.\xrightarrow{{}}\left\{ \begin{array}  {} R=1 \\  {} h=2 \\ \end{array} \right.$

Thiết diện song song với trục OO' là hình chữ nhật ABB'A' (hình bên).

Dây cung AB căng một cung 120° $\Rightarrow \widehat{AOB}={{120}^{\circ }}$

Tam giác OAB có $AB=\sqrt{O{{A}^{2}}+O{{B}^{2}}-2.OA.OB.\cos \widehat{AOB}}=\sqrt{3}$

Vì AA' là đường sinh $\xrightarrow{{}}A{A}'=h=2.$

Vậy ${{S}_{AB{B}'{A}'}}=AB.A{A}'=2.\sqrt{3}.$ Chọn C.

Lời giải chi tiết

Thiết diện song song với trục $O{O}'$là hình chữ nhật $AB{B}'{A}'$ (hình bên).

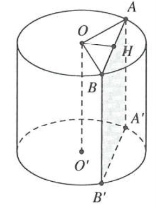
Vì $O{O}'\text{//}\left( AB{B}'{A}' \right)\Rightarrow d\left( O{O}';\left( \alpha  \right) \right)=d\left( O;\left( \alpha  \right) \right)=d\left( O;AB \right)$

Gọi H là trung điểm AB mà $OA=OB\Rightarrow OH\bot AB$

Tam giác OAH vuông tại H, có $AH=\sqrt{O{{A}^{2}}-O{{H}^{2}}}$

$=\sqrt{{{R}^{2}}-{{\left( \frac{R}{2} \right)}^{2}}}=\frac{R\sqrt{3}}{2}\xrightarrow{{}}AB=2AH=2.\frac{R\sqrt{3}}{2}=R\sqrt{3}$

Do đó $AB=R\sqrt{3},A{A}'=\frac{3R}{2}\xrightarrow[{}]{}{{S}_{AB{B}'{A}'}}=\frac{3\sqrt{3}{{R}^{2}}}{2}.$ Chọn D.

Lời giải chi tiết

Thiết diện qua trục là hình vuông ABCD (hình vẽ bên)

Suy ra $AB=BC=2\sqrt{3}\Rightarrow \left\{ \begin{array}  {} h=BC=2\sqrt{3} \\  {} R=OA=\frac{AB}{2}=\sqrt{3} \\ \end{array} \right.$

Tam giác OBM cân tại O, có $\widehat{OBM}=60{}^\circ \Rightarrow \Delta OBM.$ đều

$\Rightarrow BM=OB=\sqrt{3}\Rightarrow AM=\sqrt{A{{B}^{2}}-B{{M}^{2}}}=\sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}}=3$

Kẻ $MH\bot AB\left( H\in AB \right)$ mà $A\text{D}\bot MH\Rightarrow MH\bot \left( ABC\text{D} \right)$

Tam giác ABM vuông tại $M\Rightarrow MH=\frac{AM.BM}{AB}=\frac{3}{2}$

Diện tích tam giác ACD là ${{S}_{\Delta AC\text{D}}}=\frac{1}{2}.A\text{D}.C\text{D}=\frac{{{\left( 2\sqrt{3} \right)}^{2}}}{2}=6$

Vậy thể tích tứ diện ACDM là ${{V}_{AC\text{D}M}}=\frac{1}{3}.MH.{{S}_{\Delta AC\text{D}}}=\frac{1}{3}.\frac{3}{2}.6=3.$ Chọn B.

Lời giải chi tiết

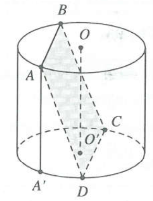
Xét hình vuông ABCD có AD không song song và không vuông góc với trục OO' của hình trụ.

Dựng đường sinh AA', ta có $\left\{ \begin{array}  {} CD\bot A{A}' \\  {} CD\bot AD \\ \end{array} \right.\Rightarrow CD\bot \left( A{A}'D \right)\Rightarrow CD\bot {A}'D$

Suy ra A'C là đường kính đáy nên ${A}'C=2\text{R}=140cm$

Xét tam giác vuông AA'C, ta có $AC=\sqrt{A{{{{A}'}}^{2}}+{A}'{{C}^{2}}}=100\sqrt{2}\text{ }cm.$

Suy ra cạnh hình vuông bằng 100 cm. Chọn B.

Lời giải chi tiết

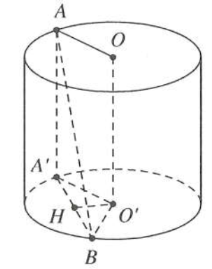
Từ hình vẽ kết hợp với giả thiết, ta có $OA=O'B=R$

Kẻ đường sinh AA' là đường sinh $\Rightarrow \left\{ \begin{array}  {} {O}'{A}'=R \\  {} A{A}'=R\sqrt{3} \\ \end{array} \right.$ và $\widehat{BA{A}'}={{30}^{0}}$

Vì $O{O}'\text{//}\left( AB{A}' \right)$ nên

$d\left( O{O}';\left( AB \right) \right)=d\left( O{O}';\left( AB{A}' \right) \right)=d\left( {O}';\left( AB{A}' \right) \right)$

Goi H là trung điểm ${A}'B\Rightarrow \left\{ \begin{array}  {} {O}'H\bot {A}'B \\  {} {O}'H\bot A{A}' \\ \end{array} \right.\Rightarrow {O}'H\bot \left( AB{A}' \right)$

Tam giác ABA' vuông tại A', có $B{A}'=A{A}'.\tan {{30}^{\circ }}=R$

Suy ra tam giác A'BO' đều có cạnh bằng R nên ${O}'H=\frac{R\sqrt{3}}{2}.$Chọn C.

Lời giải chi tiết

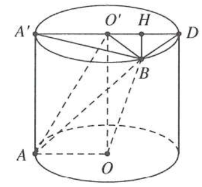
Kẻ đường sinh AA', gọi D là điểm đối xứng với A' qua tâm O'

Và H là hình chiếu của B trên A'D

Ta có $BH\bot \left( AO{O}'{A}' \right)$ nên ${{V}_{O{O}'AB}}=\frac{1}{3}{{S}_{\Delta AO{O}'}}.BH$

Xét tam giác vuông ${A}'AB,$ có ${A}'B=\sqrt{A{{B}^{2}}-A{{{{A}'}}^{2}}}=a\sqrt{3}$

Xét tam giác vuông ${A}'BD,$ có $BD=\sqrt{{A}'{{D}^{2}}-{A}'{{B}^{2}}}=a$

Suy ra $BH=\frac{a\sqrt{3}}{2}.$ Vậy ${{V}_{O{O}'AB}}=\frac{1}{3}.\left( \frac{1}{2}{{a}^{2}} \right).\frac{a\sqrt{3}}{2}=\frac{\sqrt{3}{{a}^{3}}}{12}$ (đvtt).

Chọn A.

Lời giải chi tiết

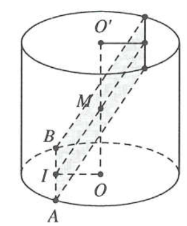
Dựa vào hình vẽ, kết hợp với giả thiết ta có

$OA=OB=R,O{O}'=2R$ và $\widehat{IM\text{O}}={{30}^{0}}$

Xét tam giác vuông MOI, có $OI=MO.\tan {{30}^{0}}=\frac{R\sqrt{3}}{3}$

Xét tam giác vuông AIO, có $IA=\sqrt{O{{A}^{2}}-O{{I}^{2}}}=\sqrt{{{R}^{2}}-{{\left( \frac{R}{\sqrt{3}} \right)}^{2}}}=\frac{R\sqrt{6}}{3}$

Suy ra $AB=2IA=\frac{2R\sqrt{6}}{3}.$ Chọn C.

Lời giải chi tiết

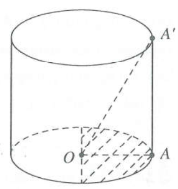
Dựng cốc hình trụ, phần gạch chéo chính là hình chiếu của diện tích bề mặt nước trong cốc (tham khảo hình vẽ bên)

Gọi S là diện tích bề mặt nước, S₀ là diện tích phần gạch chéo

Theo công thức hình chiếu, ta có $\cos \varphi =\frac{{{S}_{0}}}{S},$ với $\varphi =\widehat{\left( S;{{S}_{0}} \right)}=\widehat{{A}'OA}$

Tam giác $OA{A}'$ vuông tại A, có $\cos \widehat{{A}'OA}=\frac{OA}{O{A}'}=\frac{3}{\sqrt{{{3}^{2}}+{{15}^{2}}}}=\frac{\sqrt{26}}{26}$

Và ${{S}_{0}}=\frac{\pi {{R}^{2}}}{2}=\frac{9\pi }{2}\xrightarrow{{}}S=\frac{9\pi }{2}:\frac{\sqrt{26}}{26}=\frac{9\sqrt{26}\pi }{2}\text{ c}{{\text{m}}^{\text{2}}}\text{.}$ Chọn B.