Bài tập về lực và thời gian nén dãn có đáp án chi tiết

BÀI TẬP VỀ LỰC VÀ THỜI GIAN NÉN DÃN CỦA CLLX CÓ LỜI GIẢI CHI TIẾT

Lời giải chi tiết:

Biểu thức lực kéo về tác dụng lên vật ở vị trí li độ x là: $F=\,-kx$. Chọn B.

Lời giải chi tiết:

Ta có: F= kx $\Rightarrow $ $k=\,\frac{-F}{x}\,\left( \frac{N}{m} \right)$ . Chọn D.

Lời giải chi tiết:

Ta có : ${{F}_{h\text{ }max~~~}}=k\left| \left. \Delta {{\ell }_{o}}+A \right| \right.$.

Lại có: A = 4 cm , độ dãn của lò xo khi vật ở VTCB: $\Delta {{\ell }_{o}}=\frac{g}{{{\omega }^{2}}}=0,1m=10cm$.

Khi đó F_{đh max} = ${{F}_{h\text{ }max~~~}}=k\left| \left. \Delta {{\ell }_{o}}+A \right| \right.=m{{\omega }^{2}}.0,14=2,8N$. Chọn A .

Lời giải chi tiết:

Độ cứng $k=m{{\omega }^{2}}=16N/m$

Độ dãn của lò xo khi vật ở VTCB: $\Delta {{l}_{o}}=\frac{g}{{{\omega }^{2}}}=0,0625m=6,25cm$

Tại thời điểm $t=\frac{1}{6}\left( s \right)$ ta có: x = 2 (cm)

Chú ý chiều dương hướng lên nên khi vật có li độ x = 2 cm ta có: $\Delta \ell =\Delta {{\ell }_{o}}\,-2\,=\,4,25\,cm$

Suy ra${{F}_{h}}\,=\,k.\Delta \ell \,=\,0,68\,N$. Chọn D .

Lời giải chi tiết:

Khi vật ở vị trí biên dưới ta có: F_đh = 10 N và lực đàn hồi này là lực đàn hồi cực đại.

Vì con lắc lò xo được treo thẳng đứng nên lực đàn hồi cực đại của con lắc là :

${{F}_{h\text{ }max~}}=~k\left( \Delta {{\ell }_{o}}+A \right)=\text{ }10\text{ }N$

Mặt khác, khi con lắc ở vị trí cân bằng thì $k\Delta {{\ell }_{o}}$= mg =8 N

Suy ra kA = 2 N do đó $\Delta {{l}_{o}}>A\Rightarrow {{F}_{h\text{ }min}}~=~k\left( \Delta \ell -A \right)=\text{ }6\text{ }N$ . Chọn C .

Lời giải chi tiết:

Ta có: $f=\frac{N}{\Delta t}=\frac{100}{60}=\frac{5}{3}Hz\Rightarrow \omega =2\pi f=\frac{10}{3}\pi \left( rad/s \right)$

Theo hệ thức độc lập ta có: $A=\,\sqrt{{{x}^{2}}\,+\,{{\left( \frac{v}{\omega } \right)}^{2}}}\,=\,\,5\,\,(cm)\,$

Độ biến dạng của lò xo khi vật nằm ở vị trí cân bằng $\Delta {{\ell }_{o}}=\frac{g}{{{\omega }^{2}}}=0,09m=9cm$.

Vì $\Delta {{\ell }_{o}}>A$ nên lực đàn hồi cực đại là${{F}_{hmax~}}=k\left( \Delta {{\ell }_{o}}+A \right)$.

Lực đàn hồi cực tiểu là ${{F}_{h\max }}~=k\left( \Delta {{\ell }_{o}}-A \right)$

Vậy tỉ số cần tìm: $\frac{{{F}_{h\,max~}}}{{{F}_{\,min}}~}=\frac{k\left( \Delta {{\ell }_{o}}+A \right)}{k\left( \Delta {{\ell }_{o}}-A \right)}=\frac{9+5}{9-3}=\frac{7}{3}$ . Chọn D.

Lời giải chi tiết:

Lực đàn hồi cực đại là${{F}_{h\text{ }max}}=~k\left( \Delta l+A \right)=\text{ }10\text{ }N$.

Lực phục hồi cực đại là F_ph = kA= 6 N.

Khi đó $\left\{ \begin{matrix}kA=6N \\k.\Delta \ell =4N \\\end{matrix} \right.\Rightarrow A>\Delta \ell \Rightarrow {{F}_{h\text{ }min}}=\text{ }0\text{ }N$. Chọn D.

Lời giải chi tiết:

Ta có: $\omega =\frac{2\pi }{T}=8\pi \left( rad/s \right)$

Do con lắc nằm ngang suy ra lực đàn hồi cực đại tác dụng lên vật nặng đạt được tại vị trí biên

Suy ra ${{F}_{h\text{ }max}}=\text{ }kA\text{ }=~~m{{\omega }^{2}}A=\text{ }6,4\text{ }N$ . Chọn D .

Lời giải chi tiết:

Trong trường hợp $A\ge \Delta l$thì F_{đh min} = 0 do đó trong bài toán này $\frac{{{F}_{h\text{ }max}}}{{{F}_{h\text{ }min}}}=3\Rightarrow \Delta l>A$

Theo bài ra ta có: $\frac{{{F}_{h\text{ }max}}}{{{F}_{h\text{ }min}}}=\frac{k\left( \Delta l+A \right)}{k\left( \Delta l-A \right)}=3\Leftrightarrow A=\frac{\Delta l}{2}=\frac{g}{2{{\omega }^{2}}}=0,02m$.

Do đó tốc độ cực đại của vật là v_max = $\omega A=10\pi $ cm/s. Chọn C .

Lời giải chi tiết:

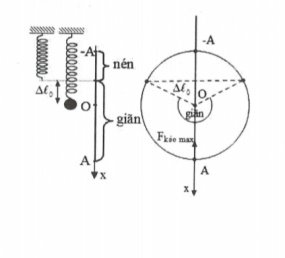
- Khoảng thời gian lò xo nén là:

$\Delta t=\frac{2\alpha }{\omega }=2.\frac{1}{\omega }\arccos \frac{\Delta {{l}_{0}}}{A}$.

- Khoảng thời gian lò xo dãn là $T-\Delta t$.

Ta có: $T=2\pi \sqrt{\frac{m}{k}}=\frac{2\pi }{25}\Rightarrow {{t}_{n\acute{e}n}}=~\frac{\pi }{75}$.

Khi đó $2.\frac{1}{\omega }.\arccos \frac{\Delta {{l}_{o}}}{A}=\frac{\pi }{75}\Rightarrow \frac{\Delta {{l}_{o}}}{A}=\frac{\sqrt{3}}{2}$.

Do đó$A=\frac{2mg}{k\sqrt{3}}\Rightarrow {{v}_{max}}=\omega A=\sqrt{\frac{m}{k}}.\frac{2g}{\sqrt{3}}~=\text{ }0,462\text{ }cm/s$.Chọn C.

Lời giải chi tiết:

Ta có: $\omega =\frac{2\pi }{T}=5\pi \left( rad/s \right)\Rightarrow \Delta {{l}_{0}}=\frac{g}{{{\omega }^{2}}}=0,04m$=4 cm.

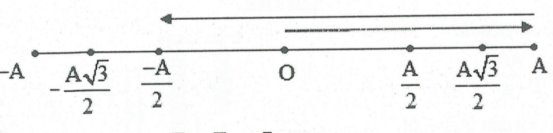Do $A>\Delta {{l}_{o}}$ nên F_{đh min} = 0 khi vật ở vị trí có li độ $x=-\Delta {{l}_{o}}=-4cm=\frac{-A}{2}$.

$$ Khi đó ta có: ${{t}_{0}}_{\to {{F}_{_{h}}}\text{ }=0}={{t}_{\left( 0\to A\to 0\to \frac{-A}{2} \right)}}=\frac{T}{2}+\frac{T}{12}=\frac{7}{30}s$ . Chọn A .

$$ $$ _{$$ $$}

Lời giải chi tiết:

Biên độ dao động của vật là $A=\frac{{{l}_{2}}-{{l}_{1}}}{2}=3cm;\omega =\frac{2\pi }{T}=5\pi \left( rad/s \right)$.

Mặt khác $\Delta l=\frac{g}{{{\omega }^{2}}}=0,04m=4cm$ .

Độ cứng của lò xo là $k=m{{\omega }^{2}}=50N/m$ .

Do $\Delta l>A$ nên lực đàn hồi cực tiểu là${{F}_{min}}=~k\left( \Delta l-A \right)=\text{ }0,5\text{ }N$. Chọn D .

Lời giải chi tiết:

Do lò xo nằm ngang nên lực đàn hồi bằng lực phục hồi.

Ta có: $\left\{ \begin{matrix}\frac{1}{2}k{{A}^{2}}=1 \\kA=10 \\\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}A=20cm \\k=50N/m \\\end{matrix} \right.$. Lại có:${{F}_{hp}}~=5\sqrt{3}=\frac{\sqrt{3}}{2}{{F}_{hp\text{ }max}}\Leftrightarrow \left| \left. x \right| \right.=\frac{A\sqrt{3}}{2}$ .

Suy ra thời gian ngắn nhất để ${{F}_{hp}}=~\frac{\sqrt{3}}{2}{{F}_{hp\text{ }max}}~$là: $\Delta t={{t}_{\left( \frac{A\sqrt{3}}{2}\to A\to \frac{A\sqrt{3}}{2} \right)}}=\frac{T}{6}=0,1\left( s \right)\Rightarrow T=0,6s$.

Thời gian $\frac{\Delta t}{T}=\frac{2}{3}\Rightarrow \Delta t=\frac{T}{2}+\frac{T}{12}+\frac{T}{12}$

Suy ra quãng đường lớn nhất vật đi được là: ${{s}_{max}}=~2A+\frac{A}{2}+\frac{A}{2}=\text{ }3A\text{ }=\text{ }60\text{ }cm$. Chọn A .

Lời giải chi tiết:

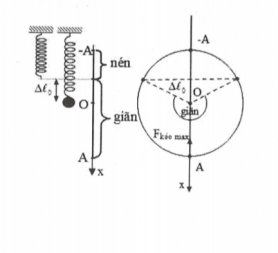
- Khoảng thời gian lò xo nén là:

$\Delta t=\frac{2\alpha }{\omega }=2.\frac{1}{\omega }.\arccos \frac{\Delta {{l}_{0}}}{A}$.

- Khoảng thời gian lò xo dãn là $T-\Delta t$ .

Suy ra : $\frac{T-\Delta t}{\Delta t}=2\Rightarrow \Delta t=\frac{T}{3}=0,4s$.

$\Rightarrow \frac{\Delta {{l}_{o}}}{A}=\cos \frac{\pi }{3}=\frac{1}{2}\Rightarrow \Delta {{l}_{0}}=\frac{A}{2}$.

Trong 1 chu kì khi vật có li độ dương F_đh và F_hp cùng chiều ( hướng về VTCB ) .

Khi x thuộc $\left[ -\frac{A}{2};0 \right]$ lực phục hồi hướng xuống dưới và lực đàn hồi hướng lên .

Khi x thuộc $\left[ -\frac{A}{2};A \right]$ lực đàn hồi và lực phục hồi đều hướng xuống .

Như vậy thời gian cần tìm là $\Delta t'=2{{t}_{\left( -\frac{A}{2}\to 0 \right)}}=2.\frac{T}{12}=\frac{T}{6}=0,2s$. Chọn D .

Lời giải chi tiết:

Theo hệ thức độc lập ta có: ${{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}$.

Khi lò xo dãn 2 cm thì $\left| \left. x \right| \right.=\left| \left. \Delta l-2 \right| \right.$ suy ra ${{\left( \Delta l-2 \right)}^{2}}={{A}^{2}}-\frac{80{{v}^{2}}}{{{\omega }^{2}}}(1)$

Hoàn toàn tương tự ta có: ${{\left( \Delta l-4 \right)}^{2}}={{A}^{2}}-\frac{72{{v}^{2}}}{{{\omega }^{2}}}(2)$; ${{\left( \Delta l-6 \right)}^{2}}={{A}^{2}}-\frac{54{{v}^{2}}}{{{\omega }^{2}}}(3)$.

Lấy (1) $-$ (2) $\Rightarrow 4\left( \Delta l-3 \right)=-\frac{8{{v}^{2}}}{{{\omega }^{2}}}$ , lấy (1) $-$ (3) $\Rightarrow 8\left( \Delta l-4 \right)=\frac{-26{{v}^{2}}}{{{\omega }^{2}}}$.

Suy ra $\frac{\Delta l-3}{2(\Delta l-4)}=\frac{8}{26}\Leftrightarrow \Delta l-3=\frac{8}{13}\Delta l-\frac{32}{13}\Leftrightarrow \Delta l=1,4$.

Đặt $b=\frac{{{v}^{2}}}{{{\omega }^{2}}}\Rightarrow \left\{ \begin{matrix}{{A}^{2}}-80b=0,36 \\{{A}^{2}}-54b=21,16 \\\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}A=\sqrt{64,36} \\b=0,8 \\\end{matrix} \right.,\omega =\sqrt{\frac{g}{\Delta l}}=\sqrt{\frac{5000}{7}}$.

- Khoảng thời gian lò xo nén là: $\Delta t=\frac{2\alpha }{\omega }=2.\frac{1}{\omega }.\arccos \frac{\Delta {{l}_{0}}}{A}=0,1044\left( s \right)$

- Khoảng thời gian lò xo dãn là: $T-\Delta t=0,13s$

Do đó $\overline{{{v}_{tb}}}=\frac{2\left( A+\Delta l \right)}{T-\Delta t}=1,45m/s$ . Chọn B .

Lời giải chi tiết:

Từ đề bài, ta tìm được chiều dài tự nhiên của lò xo là : l₀ = 3.10 = 30 cm .

Khoảng cách giữa M và N lớn nhất khi lò xo dãn cực đại, nếu chọn chiều (+) hướng xuống ta suy ra lúc