Bài tập trắc nghiệm Tỉ số thể tích khối lăng trụ có đáp án chi tiết

Bài tập trắc nghiệm Tỉ số thể tích khối lăng trụ có đáp án chi tiết
Bài tập tính thể tích khối lặng trụ sử dụng công thức simson có đáp án
| Bài tập 1: Gọi V là thể tích của hình lập phương $ABCD.{A}'{B}'{C}'{D}',{{V}_{1}}$ là thể tích tứ diện ${A}'ABD$. Hệ thức nào sau đây đúng?
A. $V=6{{V}_{1}}$ B. $V=4{{V}_{1}}$ C. $V=3{{V}_{1}}$ D. $V=2{{V}_{1}}$ |
Lời giải chi tiết
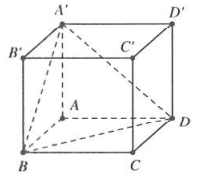
Ta có $V={{S}_{ABCD}}.A{A}'$ và ${{V}_{1}}=\frac{1}{3}{{S}_{\Delta ABD}}.A{A}'$
Mà ${{S}_{\Delta ABD}}=\frac{1}{2}{{S}_{ABCD}}\xrightarrow{{}}\frac{V}{{{V}_{1}}}=6$
Suy ra $V=6{{V}_{1}}$. Chọn A.
| Bài tập 2: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$. Gọi D là trung điểm của AC. Tính tỉ số thể tích khối tứ diện ${B}'BAD$ và thể tích khối lăng trụ đã cho.
A. $\frac{1}{4}$ B. $\frac{1}{6}$ C. $\frac{1}{12}$ D. $\frac{1}{3}$ |
Lời giải chi tiết
Ta có ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.B{B}'$ và ${{V}_{{B}'BAD}}=\frac{1}{3}{{S}_{\Delta BAD}}.B{B}'.$
Mà ${{S}_{\Delta BAD}}=\frac{1}{2}{{S}_{\Delta ABC}}\xrightarrow[{}]{}k=\frac{{{V}_{{B}'BAD}}}{{{V}_{ABC.{A}'{B}'{C}'}}}=\frac{1}{6}.$ Chọn B.
| Bài tập 3: Cho khối lăng trụ $ABC.{A}'{B}'{C}'$. Đường thẳng đi qua trọng tâm của tam giác ABC và song song với BC cắt các cạnh AB, AC lần lượt tại M, N. Mặt phẳng $\left( {A}'MN \right)$ chia khối lăng trụ thành hai phần. Tính tỉ số thể tích (phần bé chia phần lớn) của chúng.
A. $\frac{2}{3}$ B. $\frac{4}{23}$ C. $\frac{4}{9}$ D. $\frac{4}{27}$ |
Lời giải chi tiết
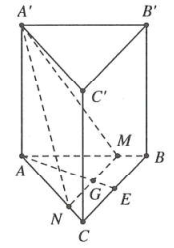
Gọi G là trọng tâm của tam giác ABC.
Gọi E là trung điểm của BC $\Rightarrow \frac{AG}{AE}=\frac{2}{3}$
Qua G kẻ đường thẳng $d//BC,$ cắt AB, AC lần lượt tại M, N.
$\Rightarrow \frac{AM}{AB}=\frac{AN}{AC}=\frac{AG}{AE}=\frac{2}{3}$ (định lí Talet)
$\Rightarrow \left\{ \begin{matrix} AM=\frac{2}{3}AB \\ AN=\frac{2}{3}AC \\\end{matrix}\Rightarrow {{S}_{\Delta AMN}}=\frac{4}{9}{{S}_{\Delta ABC}} \right.$ (1).
Ta có ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.AA'$ và ${{V}_{{A}'.AMN}}=\frac{1}{3}{{S}_{\Delta AMN}}.AA'$ (2).
Từ (1) và (2) $\Rightarrow {{V}_{{A}'.AMN}}=\frac{4}{27}{{V}_{ABC.{A}'{B}'{C}'}}\Rightarrow {{V}_{BMNC,{A}'{B}'{C}'}}=\frac{23}{27}{{V}_{ABC.{A}'{B}'{C}'}}$
Vậy tỉ số cần tìm là $\frac{4}{27}:\frac{23}{27}=\frac{4}{23}.$ Chọn B.
| Bài tập 4: Cho hình lăng trụ $ABC.{A}'{B}'{C}'$ có đáy ABC là tam giác vuông cân tại A, $AC=2\sqrt{2}.$ Biết $A{C}'$ tạo với mặt phẳng $\left( ABC \right)$ một góc $60{}^\circ $ và $A{C}'=4$. Tính thể tích của khối đa diện $ABC{C}'{B}'$.
A. $\frac{8\sqrt{3}}{3}$ B. $\frac{\sqrt{3}}{3}$ C. $2\sqrt{3}$ D. $\frac{16\sqrt{3}}{3}$ |
Lời giải chi tiết
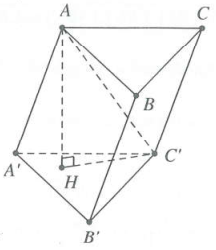
Gọi H là hình chiếu của A trên mặt phẳng $\left( {A}'{B}'{C}' \right)$.
Suy ra $H{C}'$ là hình chiếu của $A{C}'$ trên mặt phẳng $\left( {A}'{B}'{C}' \right)$.
Do đó $\widehat{\left( A{C}';\left( ABC \right) \right)}=\widehat{\left( A{C}';H{C}' \right)}=\widehat{AH{C}'}=60{}^\circ $
Tam giác $AH{C}'$, có $AH=A{C}'\sin \widehat{A{C}'H}=2\sqrt{3}$
Diện tích tam giác ${{S}_{\Delta ABC}}=\frac{A{{C}^{2}}}{2}=4$
Suy ra ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.AH=8\sqrt{3}$
Ta có ${{V}_{A.{A}'{B}'{C}'}}=\frac{1}{3}{{S}_{\Delta {A}'{B}'{C}'}}.AH=\frac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}=\frac{8\sqrt{3}}{3}.$
Suy ra ${{V}_{ABC{C}'{B}'}}={{V}_{ABC.{A}'{B}'{C}'}}-{{V}_{A.{A}'{B}'{C}'}}=\frac{16\sqrt{3}}{3}$. Chọn D.
| Bài tập 5: Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ có thể tích V. Các điểm M, N, P lần lượt thuộc các cạnh $AC,A{B}',A{D}'$ sao cho $AM=2AC,AN=3A{B}',AP=4A{D}'.$ Tính thể tích của khối tứ diện $AMNP$ theo V.
A. ${{V}_{AMNP}}=8V$ B. ${{V}_{AMNP}}=4V$ C. ${{V}_{AMNP}}=6V$ D. ${{V}_{AMNP}}=12V$ |
Lời giải chi tiết
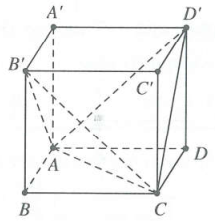
Ta có $V={{V}_{A{B}'{D}'{C}'}}+\left( {{V}_{A{A}'{B}'{D}'}}+{{V}_{C{C}'{B}'{D}'}}+{{V}_{{D}'DAC}}+{{V}_{{B}'BAC}} \right).$
Mà ${{V}_{A{A}'{B}'{D}'}}={{V}_{C{C}'{B}'{D}'}}={{V}_{{D}'DAC}}={{V}_{{B}'BAC}}=\frac{V}{6}.$
Suy ra ${{V}_{A{B}'{D}'{C}'}}=\frac{V}{3}.$
Từ gia thiết, ta có $\frac{A{B}'}{AN}=\frac{1}{3};\frac{AC}{AM}=\frac{1}{2};\frac{A{D}'}{AP}=\frac{1}{4}.$
Ta có $\frac{{{V}_{A.{B}'{D}'{C}'}}}{{{V}_{A.NPM}}}=\frac{A{B}'}{AN}.\frac{A{D}'}{AP}.\frac{AC}{AM}=\frac{1}{24}.$
$\xrightarrow{{}}{{V}_{A.NPM}}=24{{V}_{A.{B}'{D}'{C}'}}=24.\frac{V}{3}=8V.$ Chọn A.
Nhận xét: Công thức giải nhanh: Thể tích của khối tứ diện (4 đỉnh nằm trên hai đường chéo của hai mặt đối diện) có thể tích bằng $\frac{1}{3}$của khối lăng trụ tam giác.
| Bài tập 6: Cho lăng trụ tam giác đều $ABC.{A}'{B}'{C}'$ có góc giữa hai mặt phẳng $\left( {A}'BC \right)$ và $\left( ABC \right)$ bằng $30{}^\circ $. Điểm M nằm trên cạnh $A{A}'$. Biết cạnh $AB=a\sqrt{3},$ thể tích khối đa diện $MBC{C}'{B}'$ bằng
A. $\frac{3{{a}^{3}}}{4}.$ B. $\frac{3{{a}^{3}}\sqrt{3}}{2}.$ C. $\frac{3{{a}^{3}}\sqrt{2}}{4}.$ D. $\frac{2{{a}^{3}}}{3}.$ |
Lời giải chi tiết
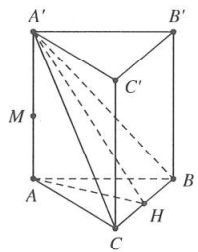
Gọi V là thể tích khối lăng trụ $ABC.{A}'{B}'{C}'$.
Do $A{A}'//B{B}'\Rightarrow {{V}_{M.BC{B}'{C}'}}={{V}_{{A}'.BC{C}'{B}'}}=V-{{V}_{{A}'.ABC}}=V-\frac{V}{3}=\frac{2V}{3}$
Dựng $AH\bot BC$ mà $A{A}'\bot BC\Rightarrow BC\bot \left( {A}'HA \right)$
Do đó $\widehat{\left( {A}'BC \right);\left( ABC \right)}=\widehat{{A}'HA}=30{}^\circ \Rightarrow AH=\frac{AB\sqrt{3}}{2}=\frac{3a}{2}.$
Khi đó $A{A}'=AH.\tan 30{}^\circ =\frac{a\sqrt{3}}{2}\Rightarrow V=A{A}'.{{S}_{\Delta ABC}}=\frac{9{{a}^{3}}}{8}.$
Vậy thể tích cần tính là ${{V}_{M.BC{C}'{B}'}}=2\frac{V}{3}=\frac{3{{a}^{3}}}{4}.$ Chọn A.
| Bài tập 7: Cho hình lăng trụ $ABC.{A}'{B}'{C}'$ có thể tích bằng V. Các điểm M, N, P lần lượt thuộc các cạnh $A{A}',B{B}',C{C}'$ sao cho $\frac{AM}{A{A}'}=\frac{1}{2};\frac{BN}{B{B}'}=\frac{CP}{C{C}'}=\frac{2}{3}.$ Tính thể tích của khối đa diện $ABC.MNP$
A. ${V}'=\frac{2}{3}V$ B. ${V}'=\frac{9}{16}V$ C. ${V}'=\frac{20}{27}V$ D. ${V}'=\frac{11}{18}V$ |
Lời giải chi tiết
Công thức giải nhanh ${{V}_{ABC.MNP}}=\left( \frac{m+n+p}{3} \right)V$ với $m=\frac{AM}{A{A}'},n=\frac{BN}{B{B}'},p=\frac{CP}{C{C}'}.$
Áp dụng với: $m=\frac{1}{2};n=\frac{2}{3};p=\frac{2}{3},$ ta được ${{V}_{ABC.MNP}}=\frac{11}{18}V$. Chọn D.
| Bài tập 8: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ cạnh 2a, gọi M là trung điểm của $B{B}'$ và P thuộc cạnh $D{D}'$sao cho $DP=\frac{1}{4}D{D}'$. Mặt phẳng $\left( AMP \right)$ cắt $C{C}'$ tại N. Thể tích khối đa diện AMNPBCD bằng
A. $V=2{{a}^{3}}$ B. $V=3{{a}^{3}}$ C. $V=\frac{11{{a}^{3}}}{3}$ D. $V=\frac{9{{a}^{3}}}{4}$ |
Lời giải chi tiết
Áp dụng công thức tính nhanh, ta được
$\frac{{{V}_{AMNPBCD}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}'}}}=\frac{1}{2}\left( \frac{BM}{B{B}'}+\frac{DP}{D{D}'} \right)=\frac{1}{2}.\left( \frac{1}{2}+\frac{1}{4} \right)=\frac{3}{8}\xrightarrow{{}}{{V}_{AMNPBCD}}=\frac{3}{8}.{{\left( 2a \right)}^{3}}=3{{a}^{3}}$. Chọn B
| Bài tập 9: Cho hình hộp $ABCD.{A}'{B}'{C}'{D}'$. Gọi M là điểm thuộc $C{C}'$ thỏa mãn $C{C}'=4CM$. Mặt phẳng $\left( A{B}'M \right)$ chia khối hộp thành hai phần có thể tích là ${{V}_{1}}$ và ${{V}_{2}}$. Gọi ${{V}_{1}}$ là phần thể tích có chứa điểm B. Tính tỉ số $k=\frac{{{V}_{1}}}{{{V}_{2}}}$.
A. $k=\frac{7}{32}$ B. $k=\frac{7}{16}$ C. $k=\frac{7}{25}$ D. $k=\frac{25}{32}$. |
Lời giải chi tiết
Trong mặt phẳng $\left( CD{D}'{C}' \right),$kẻ $MN//{C}'D.$ Suy ra $CN=\frac{1}{4}CD$ và ${{V}_{1}}$ là khối đa diện $AB{B}'NCM.$
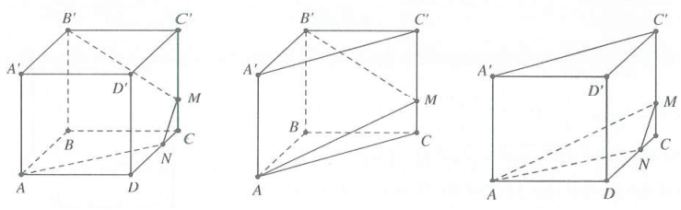
Ta chia khối hộp thành hai phần (như hình vẽ). Khi đó ${{V}_{AB{B}'.NCM}}={{V}_{AB{B}'CM}}+{{V}_{MACN}}.$
- ${{V}_{AB{B}'CM}}=\frac{0+\frac{1}{4}+1}{3}.{{V}_{ABC.{A}'{B}'{C}'}}=\frac{5}{12}.\left( \frac{1}{2}V \right)$
- ${{V}_{MACN}}=\frac{1}{4}.\frac{1}{4}{{V}_{{C}'.ADC}}=\frac{1}{16}.\left( \frac{1}{3}{{V}_{ADC.{A}'{D}'{C}'}} \right)=\frac{1}{96}V.$
Vậy ${{V}_{1}}={{V}_{ABCM{B}'}}+{{V}_{MACN}}=\frac{7}{32}V\xrightarrow{{}}{{V}_{2}}=\frac{25}{32}\xrightarrow{{}}\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{7}{25}.$Chọn C
Nhận xét: Ta có ${{V}_{MACN}}=\frac{1}{4}.\frac{1}{4}{{V}_{{C}'.ADC}}$ vì diện tích giảm 4 lần và chiều cao giảm 4 lần
| Bài tập 10: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ cạnh a. Gọi M là trung điểm của ${A}'{B}',$ N là trung điểm của BC. Tính thể tích của khối tứ diện ADMN.
A. $V=\frac{{{a}^{3}}}{3}.$ B. $V=\frac{{{a}^{3}}}{12}.$ C. $V=\frac{{{a}^{3}}}{6}.$ D. $V=\frac{{{a}^{3}}}{2}.$ |
Lời giải chi tiết
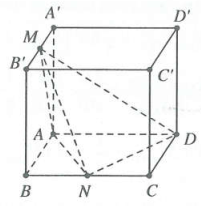
Ta có ${{V}_{ADMN}}={{V}_{M.ADN}}=\frac{1}{3}.d\left( M;\left( ABCD \right) \right).{{S}_{\Delta AMD}}$
Lại có $d\left( M;\left( ABCD \right) \right)=d\left( {A}';\left( ABCD \right) \right)=A{A}'$
Và ${{S}_{\Delta AMD}}={{S}_{ABCD}}-{{S}_{\Delta ABN}}-{{S}_{\Delta CDN}}={{S}_{ABCD}}-\frac{1}{2}{{S}_{ABCD}}=\frac{1}{2}{{S}_{ABCD}}$
Do đó ${{V}_{ADMN}}=\frac{1}{3}.A{A}'.\frac{1}{2}{{S}_{ABCD}}=\frac{1}{6}A{A}'.{{S}_{ABCD}}=\frac{{{V}_{ABCD.{A}'{B}'{C}'{D}'}}}{6}=\frac{{{a}^{3}}}{6}.$
Chọn C.
| Bài tập 11: Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ có $AB=a,AD=2a.$ Diện tích tam giác ${A}'DC$ bằng $\frac{{{a}^{2}}\sqrt{13}}{2}.$ Tính thể tích khối chóp ${A}'.BC{C}'{B}'$ theo a.
A. ${{a}^{3}}$ B. $2{{a}^{3}}$ C. $3{{a}^{3}}$ D. $6{{a}^{3}}$ |
Lời giải chi tiết
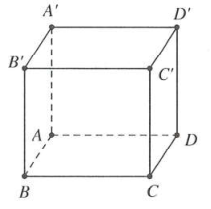
Ta có $\left\{ \begin{matrix} CD\bot D{D}' \\ CD\bot AD \\\end{matrix}\Rightarrow CD\bot \left( AD{D}'{A}' \right)\Rightarrow CD\bot {A}'D. \right.$
Suy ra ${{S}_{\Delta {A}'CD}}=\frac{1}{2}.{A}'D.CD=\frac{{{a}^{2}}\sqrt{13}}{2}\xrightarrow{{}}{A}'D=a\sqrt{13}$
Do đó $A{A}'=\sqrt{{A}'{{D}^{2}}-A{{D}^{2}}}=\sqrt{{{\left( a\sqrt{13} \right)}^{2}}-{{\left( 2a \right)}^{2}}}=3a.$
Thể tích của khối hộp $ABCD.{A}'{B}'{C}'{D}'$ là $V=A{A}'.AB.AD=6{{a}^{3}}$.
Lại có ${{V}_{{A}'.BC{C}'{B}'}}=\frac{1}{3}{{V}_{ABCD.{A}'{B}'{C}'{D}'}}=\frac{1}{3}.6{{a}^{3}}=2{{a}^{3}}.$ Chọn B.
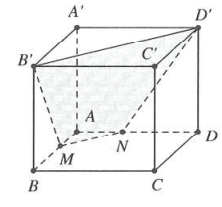
| Bài tập 12: Cho khối hộp $ABCD.{A}'{B}'{C}'{D}'$. Gọi M thuộc cạnh AB sao cho $MB=2MA.$ Mặt phẳng $\left( M{B}'{D}' \right)$ chia khối hộp thành hai phần. Tính tỉ số thể tích của hai phần đó.
A. $\frac{5}{12}.$ B. $\frac{7}{17}.$ C. $\frac{13}{41}.$ D. $\frac{5}{17}.$ |
Lời giải chi tiết
Lý thuyết bổ sung:
Cho hình chóp cụt $ABC.{A}'{B}'{C}'$ có chiều cao h, ${{S}_{1}}$ là diện tích tam giác ABC, ${{S}_{2}}$ là diện tích tam giác ${A}'{B}'{C}'.$ Thể tích khối chóp cụt $ABC.{A}'{B}'{C}'$ là $$
Qua M kẻ đường thẳng $d//BD,$ cắt AD tại N
Suy ra thiết diện cắt bởi mặt phẳng $\left( M{B}'{D}' \right)$ là $MN{D}'{B}'$
Khi đó ${{V}_{ABCD.{A}'{B}'{C}'{D}'}}={{V}_{AMN.{A}'{B}'{D}'}}+{{V}_{{B}'{C}'{D}'.MBCDN}}$
Đặt $A{A}'=h;{{S}_{ABCD}}=S\xrightarrow{{}}{{V}_{ABCD.{A}'{B}'{C}'{D}'}}=S.h$
Áp dụng công thức tính thể tích chóp cụt, ta có
${{V}_{AMN.{A}'{B}'{D}'}}=\frac{1}{3}A{A}'.\left( {{S}_{\Delta AMN}}+{{S}_{\Delta {A}'{B}'{D}'}}+\sqrt{{{S}_{\Delta AMN}}.{{S}_{\Delta {A}'{B}'{D}'}}} \right)$
Mà $\frac{{{S}_{\Delta AMN}}}{{{S}_{\Delta ABD}}}=\frac{AM}{AB}.\frac{AN}{AD}=\frac{1}{9}\Rightarrow {{S}_{\Delta AMN}}=\frac{1}{9}{{S}_{\Delta ABD}}=\frac{S}{18}.$
Và ${{S}_{\Delta {A}'{B}'{D}'}}=\frac{S}{2}\xrightarrow{{}}{{V}_{AMN.{A}'{B}'{D}'}}=\frac{1}{3}h\left( \frac{S}{18}+\frac{S}{2}+\sqrt{\frac{S}{18}.\frac{S}{2}} \right)=\frac{13}{54}V$
Vậy tỉ số thể tích cần tính là $\frac{13}{54}:\left( 1-\frac{13}{54} \right)=\frac{13}{41}.$ Chọn C.
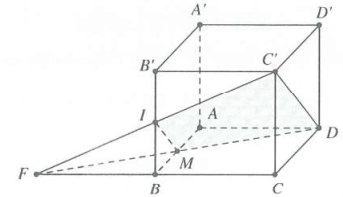
| Bài tập 13: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$. Gọi I là trung điểm của $B{B}',$ mặt phẳng $\left( DI{C}' \right)$ chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng
A. $\frac{3}{8}$ B. $\frac{2}{3}$ C. $\frac{7}{17}.$ D. $\frac{5}{12}$ |
Lời giải chi tiết
Tham khảo hình vẽ dưới đây:
Đặt $A{A}'=h;{{S}_{ABCD}}=S\xrightarrow{{}}{{V}_{ABCD.{A}'{B}'{C}'{D}'}}=S.h$
Nối $I{C}'$ cắt BC tại F; nối FD cắt AB tại M.
Suy ra $mp\left( DI{C}' \right)$ chia khối lập phương thành hai khối $IBM.{C}'CD$ và $IMA{A}'{B}'.{C}'D{D}'$
Vì M là trung điểm của AB mà $BM//CD\Rightarrow \frac{FB}{FC}=\frac{1}{2}.$
Ta có $BI//C{C}'\Rightarrow \frac{IB}{C{C}'}=\frac{FB}{FC}=\frac{1}{2}\Rightarrow {{S}_{\Delta IBM}}=\frac{1}{4}{{S}_{\Delta BA{B}'}}=\frac{1}{8}{{S}_{AB{B}'{A}'}}$
Áp dụng công thức tính thể tích chóp cụt, ta được
${{V}_{IBM.{C}'CD}}=\frac{1}{3}BC.\left( {{S}_{\Delta IBM}}+{{S}_{\Delta {C}'CD}}+\sqrt{{{S}_{\Delta IBM}}.{{S}_{\Delta {C}'CD}}} \right)=\frac{1}{3}h.\left( \frac{S}{8}+\frac{S}{2}+\sqrt{\frac{S}{8}.\frac{S}{2}} \right)=\frac{7}{24}.Sh$
Do đó, thể tích khối $IMA{A}'{B}'.{C}'D{D}'$ là ${{V}_{IMA{A}'{B}'.{C}'D{D}'}}=V-\frac{7}{24}V=\frac{17}{24}V.$
Vậy tỉ số cần tính là $\frac{7}{24}:\frac{17}{24}=\frac{7}{17}.$ Chọn C.
| Bài tập 14: Cho khối lăng trụ $ABC.{A}'{B}'{C}'$ có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng $A{A}'$ và $B{B}'$. Đường thẳng CM cắt đường thẳng ${C}'{A}'$ tại P, đường thẳng CN cắt đường thẳng ${C}'{B}'$ tại Q. Thể tích của khối đa diện lồi ${A}'MP{B}'NQ$ bằng:
A. 1 B. $\frac{1}{3}$ C. $\frac{1}{2}$ D. $\frac{2}{3}$ |
Lời giải chi tiết
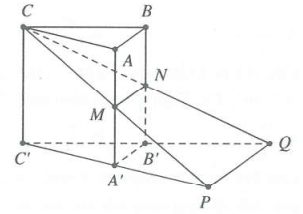
Ta có: ${{V}_{C.ABNM}}=\frac{1}{2}{{V}_{C.AB{B}'{A}'}}=\frac{1}{2}.\frac{2}{3}{{V}_{ABC.{A}'{B}'{C}'}}=\frac{1}{3}.$
Suy ra ${{V}_{CMN.{A}'{B}'{C}'}}={{V}_{ABC.{A}'{B}'{C}'}}-{{V}_{C.ABNM}}=1-\frac{1}{3}=\frac{2}{3}.$
Lại có ${{V}_{C.{C}'PQ}}={{V}_{CMN.{A}'{B}'{C}'}}+{{V}_{{A}'MP{B}'NQ}}$
$\Rightarrow {{V}_{{A}'MP{B}'NQ}}={{V}_{C.{C}'PQ}}-\frac{2}{3}.$ Mà ${{S}_{\Delta {C}'PQ}}=4{{S}_{{A}'{B}'{C}'}}$
$\Rightarrow {{V}_{C.{C}'PQ}}=4{{V}_{{C}'.{A}'{B}'{C}'}}=4.\frac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}=\frac{4}{3}.$
Vậy ${{V}_{{A}'MP{B}'NQ}}=\frac{4}{3}-\frac{2}{3}=\frac{2}{3}.$ Chọn D.
TOÁN LỚP 12
