Bài tập tính Thể tích khối chóp có mặt bên vuông góc với đáy có đáp án chi tiết

Bài tập tính Thể tích khối chóp có mặt bên vuông góc với đáy có đáp án chi tiết
Phương pháp giải bài tập tính thể tích khối chóp có mặt bên vuông góc với đáy
Giả sử hình chóp S.ABC có mặt phẳng $(SAB)\bot (ABC)$. Ta dựng $SH\bot AB$(trong trường hợp $\Delta SAB$cân tại S thì H là trung điểm của AB).
Khi đó $\left\{ \begin{array} {} (SAB)\bot (ABC) \\ {} SH\bot AB \\ {} AB=\left( SAB \right)\cap \left( ABC \right) \\ \end{array} \right.\Rightarrow SH\bot \left( ABC \right)$.
Bài tập trắc nghiệm tính thể tích có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB=$a\sqrt{3}$, BC= a. Tam giác SAC cân tại S và thuộc mặt phẳng vuông góc với đáy, mặt phẳng (SAB) tạo với đáy một góc bằng ${{60}^{o}}$. Thể tích khối chóp S.ABC là:
A. $\frac{{{a}^{3}}\sqrt{3}}{2}$. B. $\frac{{{a}^{3}}}{4}$. C. $\frac{{{a}^{3}}\sqrt{3}}{3}$ . D.$2{{a}^{3}}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của AC ta có $SH\bot AC$
Mặt khác $\left( SAC \right)\bot \left( ABC \right)$suy ra $SH\bot \left( ABC \right)$ Dựng $HE\bot AB$ khi đó HE là đường trung bình của tam giác ABC. Do đó: $HE=\frac{BC}{2}=\frac{a}{2}$ Mặt khác: $\left\{ \begin{array} {} AB\bot HE \\ {} AB\bot SH \\ \end{array} \right.\Rightarrow AB\bot (SHE)\Rightarrow \widehat{SEH}=60{}^\circ $. |
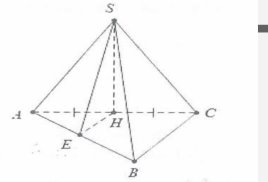 |
Do đó $SH=HE.\tan 60{}^\circ =\frac{a\sqrt{3}}{2},{{S}_{ABC}}=\frac{AB.BC}{2}=\frac{{{a}^{2}}\sqrt{3}}{2}$$\Rightarrow $ ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}}{4}$. Chọn B.
| Bài tập 2: Cho hình chóp S.ABC có đáy là tam giác ABC có AB= AC= 2a và BC= $2a\sqrt{3}$, gọi M là trung điểm của BC. Tam giác SAM cân tại S và thuộc mặt phẳng vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBC) bằng $\frac{a\sqrt{3}}{2}$. Thể tích khối chóp S.ABC là:
A. $\frac{{{a}^{3}}}{6}$. B. $\frac{3{{a}^{3}}}{2}$. C. $\frac{{{a}^{3}}\sqrt{3}}{2}$ . D.$\frac{{{a}^{3}}}{2}$. |
Lời giải chi tiết:
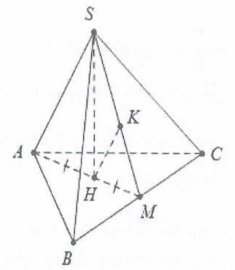
| Gọi H là trung điểm của AM ta có $SH\bot AM$
Mặt khác $\left( SAM \right)\bot \left( ABC \right)$nên $SH\bot \left( ABC \right)$ Ta có: $BM=MC=a\sqrt{3}\Rightarrow AM=\sqrt{A{{B}^{2}}-B{{M}^{2}}}=a$ $\Rightarrow {{S}_{ABC}}=\frac{1}{2}AM.BC={{a}^{2}}\sqrt{3}$. Dựng $HK\bot SM\Rightarrow HK\bot \left( SBC \right)$. Khi đó $d\left( A;\left( SBC \right) \right)=2d\left( H;\left( SBC \right) \right)=2HK$ $\Rightarrow HK=\frac{a\sqrt{3}}{4}\Rightarrow \frac{1}{S{{H}^{2}}}=\frac{1}{H{{K}^{2}}}-\frac{1}{H{{M}^{2}}}\Rightarrow SH=\frac{a\sqrt{3}}{2}$. ${{S}_{ABC}}={{a}^{2}}\sqrt{3}.$Do đó ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}}{2}$. Chọn D. |
 |
Bài tập 3: Cho khối chóp S.ABC có đáy là tam giác ABC vuông tại A, tam giác SAB vuông tại S và thuộc mặt phẳng vuông góc với đáy. Biết SA=$a\sqrt{6}$, SB= $a\sqrt{3}$ và AC=$2a$. Thể tích khối chóp S.ABC là:
|
Lời giải chi tiết:
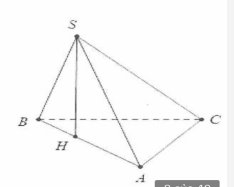
| Dựng $SH\bot AB$. Mặt khác $\left( SAB \right)\bot \left( ABC \right)$ suy ra $SH\bot \left( ABC \right)$. Ta có: $AB=\sqrt{S{{A}^{2}}+S{{B}^{2}}}=3a$. Áp dụng hệ thức lượng trong tam giác vuông SAB ta có: $HA=\frac{S{{A}^{2}}}{AB}=2a$
$\Rightarrow SH=\sqrt{S{{A}^{2}}-H{{A}^{2}}}=a\sqrt{2},{{S}_{ABC}}=\frac{AB.AC}{2}=3{{a}^{2}}$. Khi đó ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}={{a}^{3}}\sqrt{2}$.Chọn A. |
 |
| Bài tập 4: Cho hình chóp S.ABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), SAB là tam giác đều cạnh $a\sqrt{3}$, BC= $a\sqrt{3}$,đường thẳng SC tạo với mặt phẳng (ABC) góc $60{}^\circ $. Thể tích của khối chóp S.ABC bằng:
A.$\frac{{{a}^{3}}\sqrt{3}}{3}$. B. $2{{a}^{3}}\sqrt{6}$. C. $\frac{{{a}^{3}}\sqrt{6}}{2}$. D.$\frac{{{a}^{3}}\sqrt{6}}{6}$. |
Lời giải chi tiết:
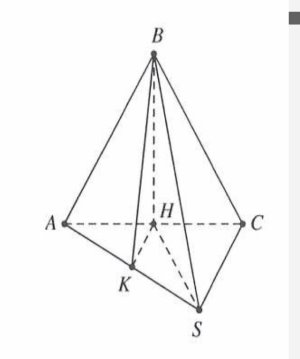
Ta có $\widehat{SC;\left( ABC \right)}=\widehat{\left( SC;AC \right)}=\widehat{SCA}=60{}^\circ $.
Gọi H là trung điểm của AB mà $\Delta ABC$ cân $\Rightarrow BH\bot \left( SAC \right)$.
Gọi K là trung điểm của SA mà $\Delta SAB$ đều $\Rightarrow BK\bot SA$
Suy ra $SA\bot \left( BHK \right)\Rightarrow SA\bot HK$ mà $HK\parallel SC\Rightarrow SA\bot SC$ .
Tam giác SAC vuông tại S, có $\widehat{SCA}=60{}^\circ \Rightarrow SC=SH=\frac{AC}{2}=a$.
Diện tích tam giác ABC là ${{S}_{\Delta ABC}}=\frac{1}{2}.AB.AC=\frac{{{a}^{2}}\sqrt{3}}{2}$.
Tam giác ABH vuông tại H, có $BH=\sqrt{A{{B}^{2}}-A{{H}^{2}}}=a\sqrt{2}$ Vậy thể tích khối chóp S.ABC là $V=\frac{1}{3}.BH.{{S}_{\Delta ABC}}=\frac{{{a}^{3}}\sqrt{6}}{6}$. Chọn D.
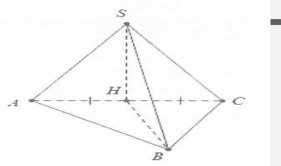
| Bài tập 5: Cho khối chóp S.ABC có đáy là tam giác đều. Tam giác SAC cân tại S và thuộc mặt phẳng vuông góc với đáy, đường thẳng SB tạo với đáy một góc $60{}^\circ $. Biết khoảng cách từ S đến mặt đáy (ABC) là h. Thể tích khối chóp tính theo h là:
A. $\frac{{{h}^{3}}\sqrt{3}}{3}$. B. $\frac{{{h}^{3}}\sqrt{3}}{9}$. C. $\frac{{{h}^{3}}\sqrt{3}}{27}$. D.$\frac{{{h}^{3}}\sqrt{3}}{18}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của AC ta có $SH\bot AC$
Mặt khác $\left( SAC \right)\bot \left( ABC \right)$ nên $SH\bot \left( ABC \right)$ Khi đó SH= $h$. Mặt khác $\widehat{SBH}=60{}^\circ $ Do vậy $HB\tan 60{}^\circ =h\Rightarrow HB=\frac{h}{\sqrt{3}}$. |
 |
Đặt AB=$a\Rightarrow HB=\frac{a\sqrt{3}}{2}=\frac{h}{\sqrt{3}}\Rightarrow a=\frac{2h}{3}$. Do đó ${{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{h}^{2}}\sqrt{3}}{9}\Rightarrow $ ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{h}^{3}}\sqrt{3}}{27}$. Chọn C.
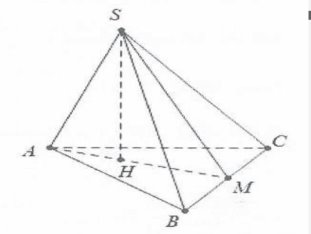
| Bài tập 6: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Gọi M là trung điểm của BC. Tam giác SAM vuông tại S và thuộc mặt phẳng vuông góc với đáy. Biết SA=$\frac{a}{\sqrt{2}}$, thể tích khối chóp S.ABC là:
A. $\frac{{{a}^{3}}\sqrt{2}}{4}$. B. $\frac{{{a}^{3}}\sqrt{2}}{12}$. C. $\frac{{{a}^{3}}\sqrt{2}}{18}$. D.$\frac{{{a}^{3}}\sqrt{2}}{24}$. |
Lời giải chi tiết:
| Dựng $SH\bot AM$ta có $\left( SAM \right)\bot \left( ABC \right)$nên $SH\bot \left( ABC \right)$
Mặt khác $AM=\frac{a\sqrt{3}}{2}$ Suy ra $SM=\sqrt{A{{M}^{2}}-S{{A}^{2}}}=\frac{a}{2}$ Lại có: $SH=\frac{SA.SM}{\sqrt{S{{A}^{2}}+S{{M}^{2}}}}=\frac{a}{\sqrt{6}}$ Vậy ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}\sqrt{2}}{24}$. Chọn D. |
 |
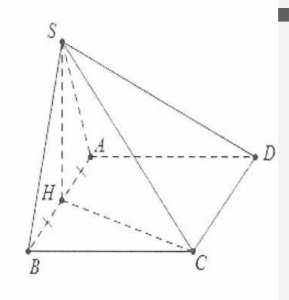
| Bài tập 7: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAB đều cạnh $2a$ và thuộc mặt phẳng vuông góc với đáy. Đường thẳng SC tạo với đáy một góc $30{}^\circ $. Thể tích khối chóp S.ABCD là:
A. $\frac{4{{a}^{3}}\sqrt{6}}{3}$. B. $\frac{2{{a}^{3}}\sqrt{6}}{3}$. C. $\frac{4{{a}^{3}}\sqrt{6}}{6}$. D.$\frac{4{{a}^{3}}\sqrt{2}}{3}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của AB ta có $SH\bot AB$.
Mặt khác $\left( SAB \right)\bot \left( ABC \right)$ nên $SH\bot \left( ABC \right),SH=a\sqrt{3}$. Đường thẳng SC tạo với đáy một góc $30{}^\circ $ Do đó $HC\tan 30{}^\circ =SH\Rightarrow HC=3a$. Khi đó $BC=\sqrt{H{{C}^{2}}-H{{B}^{2}}}=2a\sqrt{2}$ Do vậy ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{4{{a}^{3}}\sqrt{6}}{3}$.Chọn A. |
 |
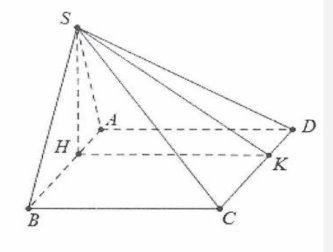
| Bài tập 8: Cho khối chóp S.ABCD có đáy là hình chữ nhật. Tam giác SAB vuông tại S và thuộc mặt phẳng đáy. Biết rằng SA= 3 và SB= 4, mặt phẳng (SCD) tạo với đáy một góc $60{}^\circ $. Thể tích khối chóp S.ABCD là:
A. $\frac{16\sqrt{3}}{15}$. B. $\frac{4\sqrt{3}}{5}$. C. $\frac{16}{5}$. D.$\frac{16\sqrt{3}}{5}$. |
Lời giải chi tiết:
| Dựng $SH\bot AB$ ta có $\left( SAB \right)\bot \left( ABC \right)$nên $SH\bot \left( ABC \right)$. Mặt khác $AB=\sqrt{S{{A}^{2}}+S{{B}^{2}}}=5$
Khi đó: $SH=\frac{SA.SB}{\sqrt{S{{A}^{2}}+S{{B}^{2}}}}=\frac{12}{5}$. Dựng $HK\bot CD$ ta có: $\left\{ \begin{array} {} CD\bot SH \\ {} CD\bot HK \\ \end{array} \right.\Rightarrow CD\bot \left( SHK \right)$ Do đó $\widehat{SKH}=60{}^\circ \Rightarrow HK\tan 60{}^\circ =SH$ $\Rightarrow HK=AD=\frac{SH}{\tan 60{}^\circ }=\frac{4\sqrt{3}}{5}$ Vậy ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{16\sqrt{3}}{5}$. Chọn D. |
 |
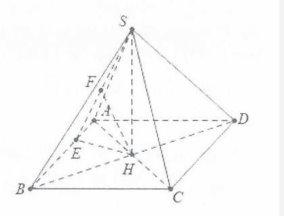
| Bài tập 9: Cho khối chóp S.ABCD có đáy là hình thoi ABCD có AC= $2a$, BD=$2a\sqrt{3}$. Tam giác SAC cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết khoảng cách từ D đến mặt phẳng (SAB) bằng $\frac{2a\sqrt{15}}{5}$.Thể tích khối chóp S.ABCD là:
A.$2{{a}^{3}}\sqrt{15}$ . B. $4{{a}^{3}}$. C. $2{{a}^{3}}\sqrt{2}$. D.$2{{a}^{3}}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của AC ta có $SH\bot AC$. Mặt khác $\left( SAC \right)\bot \left( ABC \right)$nên $SH\bot \left( ABC \right)$. Ta có:$DB=2HB$
Do vậy $d\left( D;\left( SAB \right) \right)=2d\left( H;\left( SAB \right) \right)$ Dựng $HE\bot AB$; $HF\bot SE$. Khi đó $HF=d\left( H;\left( SAB \right) \right)=\frac{1}{2}d\left( D;\left( SAB \right) \right)=\frac{a\sqrt{15}}{5}$. Lại có: $\frac{1}{H{{F}^{2}}}=\frac{1}{H{{E}^{2}}}+\frac{1}{S{{H}^{2}}}$ |
 |
Mặt khác $\begin{array} {} \frac{1}{H{{E}^{2}}}=\frac{1}{H{{A}^{2}}}+\frac{1}{H{{B}^{2}}}=\frac{4}{3{{a}^{2}}}\Rightarrow \frac{1}{S{{H}^{2}}}=\frac{1}{H{{F}^{2}}}-\frac{1}{H{{E}^{2}}}=\frac{1}{3{{a}^{2}}}\Rightarrow S{{H}^{{}}}=a\sqrt{3} \\ {} \\ \end{array}$
${{S}_{ABCD}}=\frac{AC.BD}{2}=2{{a}^{2}}\sqrt{3}\Rightarrow $ ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=2{{a}^{3}}$. Chọn D.
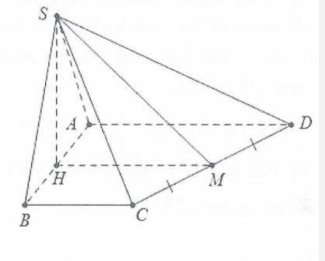
| Bài tập 10: Cho khối chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D có AB= BC=$2a$, AD= $3a$. Tam giác SAB cân tại A và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của CD. Đường thẳng SM tạo với đáy một góc $60{}^\circ $. Thể tích khối chóp S.ABCD là:
A. $\frac{25{{a}^{3}}\sqrt{3}}{6}$. B. $\frac{25{{a}^{3}}\sqrt{3}}{2}$. C.$\frac{5{{a}^{3}}\sqrt{3}}{12}$ . D.$\frac{5{{a}^{3}}\sqrt{3}}{6}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của AB ta có $SH\bot AB$.
Mặt khác $\left( SAB \right)\bot \left( ABC \right)$nên $SH\bot \left( ABC \right)$. Do $\widehat{SM;\left( ABCD \right)}=60{}^\circ \Rightarrow \widehat{SMH}=60{}^\circ $ Lại có $HM=\frac{AD+BC}{2}=\frac{5a}{2}$ $\Rightarrow SH=HM\tan \widehat{SMH}=HM\tan 60{}^\circ =\frac{5a\sqrt{3}}{2}$ Ta có ${{S}_{ABCD}}=\frac{AD+BC}{2}.AB=5{{a}^{2}}$. ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{25{{a}^{3}}\sqrt{3}}{6}$. Chọn A. |
 |
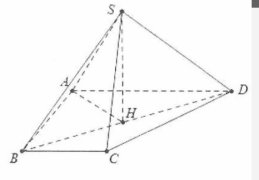
| Bài tập 11: Cho khối chóp S.ABCD có đáy là hình thang ABCD vuông tại A và B có AB= $a\sqrt{3}$, AD= $3a$, BC=$a$. Tam giác SBD cân tại S và thuộc mặt phẳng vuông góc với đáy. Đường thẳng SA tạo với đáy một góc. Thể tích khối chóp S.ABCD là:
A. $6{{a}^{3}}$. B. $\frac{2{{a}^{3}}}{3}$. C. $\frac{3{{a}^{3}}}{2}$. D.$2{{a}^{3}}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của BD ta có $SH\bot BD$. Mặt khác $\left( SBD \right)\bot \left( ABC \right)$ nên $SH\bot \left( ABC \right)$
Lại có $BD=\sqrt{A{{B}^{2}}+A{{D}^{2}}}=2a\sqrt{3}$ $\Rightarrow AH=\frac{1}{2}BD=a\sqrt{3}$. Do SA tạo với đáy góc $45{}^\circ \Rightarrow \widehat{SAH}=45{}^\circ \Rightarrow SH=a\sqrt{3}$ |
 |
Mặt khác ${{S}_{ABCD}}=\frac{AD+BC}{2}.AB=2{{a}^{2}}\sqrt{3}\Rightarrow $ ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=2{{a}^{3}}$.Chọn D.
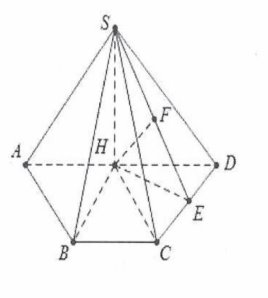
| Bài tập 12: Cho khối chóp S.ABCD có đáy là nửa lục giác đều đường kính AD= $2a$. Tam giác SAD cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng (SCD) bằng $\frac{a\sqrt{3}}{2}$. Thể tích khối chóp S.ABCD là:
A. $\frac{3{{a}^{3}}\sqrt{3}}{8}$. B.$\frac{{{a}^{3}}\sqrt{3}}{8}$ . C. $\frac{{{a}^{3}}\sqrt{3}}{2}$. D.$\frac{{{a}^{3}}\sqrt{3}}{4}$. |
Lời giải chi tiết:
| Gọi H là trung điểm của AD ta có $SH\bot AD$.
Mặt khác $\left( SAD \right)\bot \left( ABC \right)$nên $SH\bot \left( ABC \right)$. Do $AD=2HD\Rightarrow d\left( A;\left( SCD \right) \right)=2d\left( H;\left( SCD \right) \right)$. Dựng $HE\bot CD,HF\bot SE$ $\Rightarrow d\left( H;\left( SCD \right) \right)=HF=\frac{1}{2}d\left( A;\left( SCD \right) \right)=\frac{a\sqrt{3}}{4}$. Mặt khác HCD là tam giác đều cạnh $a$ nên E là trung điểm của CD và HE=$\frac{a\sqrt{3}}{2}$ Suy ra $SH=\frac{a}{2}$ $\Rightarrow $ ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{1}{3}SH.3{{S}_{HCD}}=\frac{{{a}^{3}}\sqrt{3}}{8}$. Chọn B. |
 |
TOÁN LỚP 12
