Bài tập tìm số điểm dao động với biên độ cực đại cực tiểu có đáp án chi tiết

BÀI TẬP SỐ ĐIỂM DAO ĐỘNG VỚI BIÊN ĐỘ CỰC ĐẠI, CỰC TIỂU (CĐ, CT) CÓ ĐÁP ÁN CHI TIẾT

Lời giải chi tiết

Ta có: Bước sóng $\lambda =\frac{v}{f}=\frac{20}{100}=0,2m=20cm$

Do 2 nguồn cùng pha nên số điểm không dao động trên AB là số giá trị k nguyên thỏa mãn $\frac{-AB}{\lambda }-0,5<k<\frac{AB}{\lambda }-0,5\Leftrightarrow -5<k<4\Rightarrow k=4,\pm 3,\pm 2,\pm 1,0$ có 8 giá trị của k thỏa mãn yêu cầu nên có 8 điểm trên AB không dao động. Chọn C

Lời giải chi tiết

Do 2 nguồn cùng pha nên số điểm cực đại trên AB là số giá trị k nguyên thỏa mãn

$\frac{-AB}{\lambda }<k<\frac{AB}{\lambda }\Leftrightarrow -5,33<k<5,33\Rightarrow k=\pm 5,\pm 4,...\pm 1,0$ có 11 giá trị của k thỏa mãn yêu cầu nên có 11 điểm trên AB dao động cực đại. Chọn C.

Lời giải chi tiết

Ta có: $\lambda =vT=v.\frac{2\pi }{\omega }=0,02m=2cm$

Do 2 nguồn ngược pha nên số điểm dao động cực đại trên AB là số giá trị k nguyên thỏa mãn $\frac{-AB}{\lambda }-0,5<k<\frac{AB}{\lambda }-0,5\Leftrightarrow -5,5<k<4,5\Rightarrow k=-5,\pm 4,\pm

3,\pm 2,\pm 1,0$ có 10 giá trị của k thỏa mãn yêu cầu nên có 10 điểm trên AB dao động cực đại. Chọn C.

Lời giải chi tiết

Ta có : Bước sóng $\lambda =\frac{v}{f}=\frac{45}{15}=3cm$

Do 2 nguồn cùng pha nên số điểm dao động cực đại trên AB là số giá trị k nguyên thõa mãn $\frac{-AB}{\lambda }<k<\frac{AB}{\lambda }\Leftrightarrow -3,2<k<3,2\Rightarrow k=\pm 3,\pm 2,\pm 1,0$ có 7 giá trị của k thõa mãn yêu cầu nên có 7 điểm trên đoạn AB dao động cực đại. Chọn B

Lời giải chi tiết

Ta có: f =20Hz. Bước sóng $\lambda =\frac{v}{f}=\frac{100}{20}=5cm$

Điểm dao động với biên độ 8mm là điểm dao động cực đại.

Do 2 nguồn cùng pha nên số điểm dao động cực đại trên AB là số giá trị k nguyên thỏa mãn $\frac{-AB}{\lambda }<k<\frac{AB}{\lambda }\Leftrightarrow -4,8<k<4,8\Rightarrow k=\pm 4,\pm 3,\pm 2,\pm 1,0$ có 9 giá trị của k thỏa mãn yêu cầu nên có 9 điểm trên đoạn AB dao động cực đại. Chọn B.

Lời giải chi tiết

Ta có: $\lambda =\frac{v}{f}=3cm$

Do 2 nguồn ngược pha nên số điểm dao động cực đại trên AB là số giá trị k nguyên thỏa mãn $\frac{-AB}{\lambda }-0,5<k<\frac{AB}{\lambda }-0,5\Leftrightarrow -3,83<k<2,88\Rightarrow k=-3,\pm 2,\pm 1,0$ có 4 giá trị của k thỏa mãn yêu cầu nên có 4 điểm trên AB dao động cực đại. Chọn C

Lời giải chi tiết

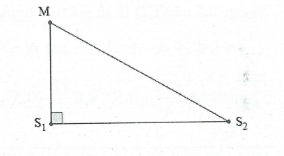
Ta có: f = 15Hz. Bước sóng $\lambda =\frac{v}{f}=\frac{75}{15}=5cm$

$\text{M}{{\text{S}}_{\text{2}}}=\sqrt{MS_{1}^{2}+{{S}_{1}}S_{1}^{2}}=30cm$

Tại M ta có: ${{d}_{2}}-{{d}_{1}}=M{{S}_{2}}-M{{S}_{1}}=14cm$

Tại S₂ ta có: ${{d}_{2}}-{{d}_{1}}=-{{S}_{1}}{{S}_{2}}=-24cm$

Do 2 nguồn cùng pha nên số cực đại qua S₂M là số giá trị k thỏa mãn.

$-24<k\lambda <14\Leftrightarrow -4,8<k<2,8\Rightarrow k=-4,-3,\pm 2,\pm 1,0\Rightarrow $có 7 giá trị của k thỏa mãn yêu cầu. Chọn A.

Lời giải chi tiết

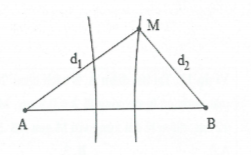
Do giữa M và trung trực của AB có 1 dãy cực đại nên M thuộc cực đại số 2

Khi đó ${{d}_{1}}-{{d}_{2}}=2\lambda \Rightarrow \lambda =3cm$

Tại M ta có: ${{d}_{1}}-{{d}_{2}}=6cm$

Tại A ta có: ${{d}_{1}}-{{d}_{2}}=-AB=-10\,cm$

Điều kiện cực tiểu: ${{d}_{1}}-{{d}_{2}}=(k+0,5)\lambda $

Cho $-\text{10 (k + 0,5)}\lambda <\text{6}\Rightarrow -\text{3,88}<\text{k}<\text{1,5}\Rightarrow \text{k}=-\text{3,}-\text{2,}\pm \text{1,0}$ có 5 điểm không dao động.

Chọn D.

Lời giải chi tiết

Ta có: f =20Hz $\Rightarrow \lambda =\frac{v}{f}=2cm$

$AC=BD=\sqrt{{{18}^{2}}+{{24}^{2}}}=30cm$

Tại D ta có: ${{d}_{1}}-{{d}_{2}}=-12cm$

Tại C ta có: ${{d}_{1}}-{{d}_{2}}=12cm$

Số cực đại trên CD là số giá trị k nguyên thỏa mãn:

$\frac{-12}{\lambda }\le k\le \frac{12}{\lambda }\Leftrightarrow -6\le k\le 6$ suy ra có 13 cực đại.

Số cực tiểu: $\frac{-12}{\lambda }-0,5\le k\le \frac{12}{\lambda }-0,5\Leftrightarrow -6,5\le k\le 5,5\Rightarrow $ có 12 cực tiểu. Chọn B

Lời giải chi tiết

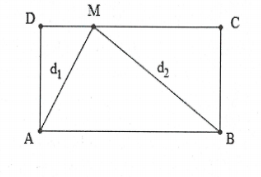
Xét điểm M trên CD: MA = d₁; MB = d₂

Điểm M có biên độ cực đại khi: ${{d}_{1}}-{{d}_{2}}=k\lambda =2k$

Ta cho: $15-15\sqrt{2}\le 2k\le 15\sqrt{2}-15$

$\Leftrightarrow -3,1\le k\le 3,1$ suy ra đoạn CD có 7 điểm có biên độ cực đại. Chọn A.

Lời giải chi tiết

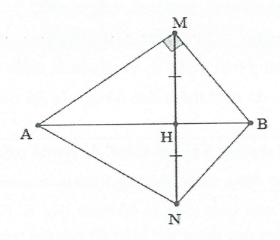
Do $A{{M}^{2}}+M{{B}^{2}}=A{{B}^{2}}$ nên tam giác AMB vuông tại M. Gọi $H=MN\cap AB$

Khi đó $AH=\frac{M{{A}^{2}}}{AB}=12,8cm$

$HB=\frac{M{{B}^{2}}}{AB}=7,2$.

Tại M có: ${{d}_{1}}-{{d}_{2}}=MA-MB=4cm$

Tại H có: ${{d}_{1}}-{{d}_{2}}=HA-HB=5,6cm$

Ta cho: $4\le 0,9k\le 5,6\Rightarrow 4,44\le k\le 6,22$

Do đó 2 cực đại trên MH nên có 4 cực đại trên MN. Chọn D.

Lời giải chi tiết

Ta có: $f=\frac{\omega }{2\pi }=20Hz,\lambda =\frac{v}{f}=\frac{30}{20}=1,5cm$

$BD=\sqrt{A{{D}^{2}}+A{{B}^{2}}}=20\sqrt{2}$

Do 2 nguồn ngược pha nên điều kiện cực đại là: ${{d}_{1}}-{{d}_{2}}=(k+0,5)\lambda =1,5(k+0,5)$

Tại D ta có: ${{d}_{1}}-{{d}_{2}}=AD-BD=20-20\sqrt{2}$

Tại B ta có: ${{d}_{1}}-{{d}_{2}}=AB=20$

Ta cho: $20-20\sqrt{2}\le 1,5(k+0,5)\le 20\Leftrightarrow -6,022\le k\le 12,833\Rightarrow k=-6,-5...12$

Do đó có 19 điểm dao động cực đại trên đoạn BD. Chọn C.

Lời giải chi tiết

Ta có: $M{{S}_{2}}=\sqrt{MS_{1}^{2}+{{S}_{1}}S_{2}^{2}}=10\sqrt{5}cm$

Bước sóng: $\lambda =vT=0,8m$

Hai nguồn cùng pha nên cực đại giao thoa thỏa mãn: ${{d}_{1}}-{{d}_{2}}=k\lambda =0,8k$

Tại điểm M ta có: ${{d}_{1}}-{{d}_{2}}=10-10\sqrt{5}$

Tại điểm S₁ ta có: ${{d}_{1}}-{{d}_{2}}=20$

Ta cho: $-20\le 0,8k\le 10-10\sqrt{5}\Rightarrow -25\le k\le -15,45.$

Chú ý loại điểm S₁ vì nguồn là điểm đặc biệt không phải cực đại (loại $k=-25$)

Do đó có 9 điểm dao động cực đại trên đoạn MS₁. Chọn C

Lời giải chi tiết

Bước sóng: $\lambda =\frac{v}{f}=2cm$

Do 2 nguồn ngược pha nên điều kiện cực đại giao thoa là : ${{d}_{1}}-{{d}_{2}}=(k+0,5)\lambda $

Tại A ta có: ${{d}_{1}}-{{d}_{2}}=-14,5cm$, tại điểm G ta có: ${{d}_{1}}-{{d}_{2}}=GA-GB=7,25cm.$

Ta cho: $-14,5\le 02(k+0,5)\le 7,25\Rightarrow -7,75\le k\le 3,125.$ Suy ra có 11 giá trị của k nguyên thỏa mãn nên có 11 điểm cực đại trên đoạn AG. Chọn A

Lời giải chi tiết

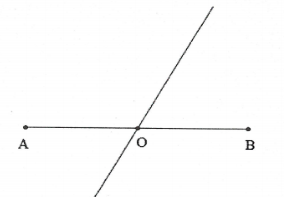
Số cực đại trên khoảng AB là số giá trị k thỏa mãn

$\frac{-Ab}{\lambda }<k<\frac{AB}{\lambda }.$

Ta có : $\lambda =\frac{v}{f}=3cm$

Khi đó: $-3,333<k<3,333$ như vậy trên AB có 7 điểm cực đại nên trên đường thẳng $\Delta $ có tối đa 7 cực đại. Dựa vào đáp án. Chọn A.

Lời giải chi tiết

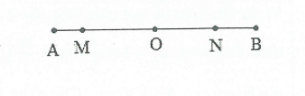
Ta có : $\lambda =\frac{v}{f}=2cm$. Điều kiện cực đại giao thoa:

${{d}_{1}}-{{d}_{2}}=k\lambda $. Tại M ta có ${{d}_{1}}-{{d}_{2}}=MA-MB$

$=(OA-OM)-(OB+OM)=-2OM=-7,5cm$

Tại N tương tự ta có: ${{d}_{1}}-{{d}_{2}}=NA-NB=(OA+ON)-(OB-ON)=2ON=4,5cm$

Ta cho: $-7,5\le 2k\le 4,5\Rightarrow -3,75\le k\le 2,25\Rightarrow $ có 6 điểm cực đại.

Tương tự số cực tiểu: $-7,5\le (k+0,5)\lambda \le 4,5\Rightarrow -4,25\le k\le 1,75$ suy ra có 6 cực tiểu. Chọn B

Lời giải chi tiết

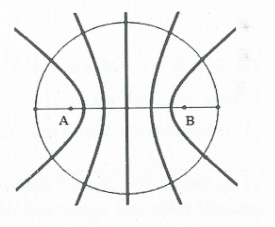
Do đường tròn tâm O có bán kính $R=12\lambda $ còn $AB=9,6\lambda $ nên đoạn AB thuộc đường tròn.

Vì hai nguồn A, B giống hệt nhau nên dao động cùng pha. Số điểm dao động với biên độ cực đại trên AB là:$\frac{-Ab}{\lambda }<k<\frac{AB}{\lambda }$

Thay số: $-\text{9,6 k 9,6}\Rightarrow $có 19 giá trị của k

Vậy nên đoạn AB có 19 điểm dao động với biên độ cực đại hay trên đường tròn tâm O có 2.19 =38 điểm. Chọn D

Lời giải chi tiết

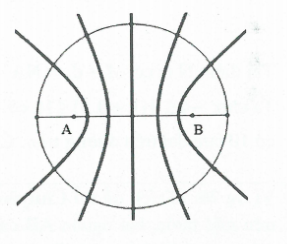
Do đường tòn tâm O có bán kính $2R>x$ nên đoạn AB thuộc đường tròn.

Vì hai nguồn A, B giống hệt nhau nên dao động cùng pha.

Số điểm dao động với biên độ cực đại trên AB là: $\frac{-AB}{\lambda }<k<\frac{AB}{\lambda }$

Thay số: $-\text{4 k 4}\Rightarrow $ có 7 giá trị của k

Vậy nên đoạn AB có 7 điểm dao động với biên độ cực đại hay trên đường tròn tâm O