Bài tập tìm cực trị của hàm số hợp có đáp án chi tiết

BÀI TẬP TÌM CỰC TRỊ CỦA HÀM SỐ HỢP CÓ ĐÁP ÁN
| Bài tập 1: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)=\left( 3-x \right)\left( {{x}^{2}}-1 \right)+2x,\forall x\in \mathbb{R}.$ Hỏi hàm số $g\left( x \right)=f\left( x \right)-{{x}^{2}}-1$ đạt cực tiểu tại điểm nào sau đây?
A. $x=-1.$ B. $x=1.$ C. $x=3.$ D. $x=0.$ |
Lời giải chi tiết
HD: Ta có $g'\left( x \right)=f'\left( x \right)-2x=\left( 3-x \right)\left( {{x}^{2}}-1 \right);g'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=3\text{ } \\ x=\pm 1 \\\end{matrix} \right.$
Lập bảng xét dấu $\xrightarrow[{}]{}$ Hàm số đạt cực tiểu tại $x=1.$Chọn B.
| Bài tập 2: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)=\left( x+3 \right)\left( 9-{{x}^{2}} \right)-3{{x}^{2}},\forall x\in \mathbb{R}.$ Hỏi hàm số $g\left( x \right)=f\left( x \right)+{{x}^{3}}-1$ đạt cực đại tại điểm nào sau đây?
A. $x=3.$ B. $x=-3.$ C. $x=0.$ D. $x=-1.$ |
Lời giải chi tiết
HD: Ta có $g'\left( x \right)=f'\left( x \right)+3{{x}^{2}}=\left( x+3 \right)\left( 9-{{x}^{2}} \right)={{\left( x+3 \right)}^{2}}\left( 3-x \right);g'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=-3\text{ } \\ x=3\text{ } \\\end{matrix} \right.$
Và $g'\left( x \right)$ không đổi dấu khi qua điểm $x=-3\Rightarrow x=3$là điểm cực đại. Chọn A.
| Bài tập 3: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{x}^{2}}-3x,\forall x\in \mathbb{R}$ và $f\left( 0 \right)\ge 10$. Giá trị cực tiểu của hàm số $g\left( x \right)=f\left( x \right)+3$ có thể bằng
A. 13. B. 12. C. 16. D. 14. |
Lời giải chi tiết
HD: Ta có $g'\left( x \right)=f'\left( x \right)={{x}^{2}}-3x;g'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=0\text{ } \\ x=3\text{ } \\\end{matrix} \right.$
Suy ra $x=3$ là điểm cực tiểu của hàm số $\Rightarrow g\left( 3 \right)<g\left( 0 \right)=f\left( 0 \right)+3<13.$ Chọn B.
| Bài tập 4: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{x}^{2}}-2x,\forall x\in \mathbb{R}.$ Hỏi hàm số $g\left( x \right)=f\left( 1-x \right)$ đạt cực đại tại điểm nào dưới đây?
A. $x=1.$ B. $x=-1.$ C. $x=0.$ D. $x=2.$ |
Lời giải chi tiết
HD: Ta có $g'\left( x \right)=-f'\left( 1-x \right)=-\left( 1-x \right)\left( -1-x \right)=\left( 1-x \right)\left( x+1 \right)$
Phương trình $g'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=1\text{ } \\ x=-1 \\\end{matrix} \right.\xrightarrow{{}}x=1$ là điểm cực đại. Chọn A.
| Bài tập 5: Cho hàm số $y=f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right)=\left( {{x}^{2}}-3x \right)\left( 1-x \right)$trên $\mathbb{R}$. Số điểm cực trị của hàm số $g\left( x \right)=f\left( {{x}^{2}}-x+1 \right)$ là
A. 5. B. 6. C. 7. D. 8. |
Lời giải chi tiết
Ta có: $f'\left( x \right)=\left( {{x}^{2}}-3x \right)\left( 1-x \right)$
Khi đó: $g'\left( x \right)=\left[ f\left( {{x}^{2}}-x+1 \right) \right]\begin{matrix} ' \\ {} \\\end{matrix}=\left( 2x-1 \right)f'\left( {{x}^{2}}-x+1 \right)=\left( 2x-1 \right)\left( {{x}^{2}}-x+1 \right)\left( {{x}^{2}}-x-2 \right)\left( x-{{x}^{2}} \right)$
$=\left( 2x-1 \right)\left( {{x}^{2}}-x+1 \right)\left( x+1 \right)\left( x-2 \right)x\left( 1-x \right)$
Do ![]() đổi dấu qua 5 điểm suy ra hàm số
đổi dấu qua 5 điểm suy ra hàm số ![]() có 5 điểm cực trị. Chọn A.
có 5 điểm cực trị. Chọn A.
| Bài tập 6: Cho hàm số $y=f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right)=\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}-4x+3 \right)$trên $\mathbb{R}$. Số điểm cực đại của hàm số $g\left( x \right)=f\left( {{x}^{2}}+2x \right)$ là
A. 1. B. 2. C. 4. D. 5. |
Lời giải chi tiết
Ta có: $f'\left( x \right)={{\left( x-1 \right)}^{2}}\left( x+1 \right)(x-3)$
Khi đó: $g'\left( x \right)=\left( 2x+2 \right)f'\left( {{x}^{2}}+2x \right)=\left( 2x+2 \right){{\left( {{x}^{2}}+2x-1 \right)}^{2}}\left( {{x}^{2}}+2x+1 \right)\left( {{x}^{2}}+2x-3 \right)$
$=\left( 2x+2 \right){{\left( {{x}^{2}}+2x-1 \right)}^{2}}{{\left( x+1 \right)}^{2}}\left( x-1 \right)\left( x+3 \right).$Ta có bảng xét dấu:

Do $g'\left( x \right)$ đổi dấu từ dương sang âm khi qua 1 điểm nên hàm số $g\left( x \right)$ có 1 điểm cực đại. Chọn A.
| Bài tập 7: Cho hàm số $y=f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right)=\left( {{x}^{2}}-4 \right)\left( {{x}^{2}}-2x \right)$trên $\mathbb{R}$. Số điểm cực tiểu của hàm số $g\left( x \right)=f\left( {{x}^{2}}+3x \right)$ là
A. 1. B. 2. C. 3. D. 4.. |
Lời giải chi tiết
Ta có: $f'\left( x \right)=\left( {{x}^{2}}-2 \right)\left( x+2 \right)x$
Khi đó: $g'\left( x \right)=\left( 2x+3 \right)f'\left( {{x}^{2}}+3x \right)=\left( 2x+3 \right){{\left( {{x}^{2}}+3x-2 \right)}^{2}}\left( {{x}^{2}}+3x+2 \right)\left( {{x}^{2}}+3x \right)$
$=\left( 2x+3 \right){{\left( {{x}^{2}}+3x-2 \right)}^{2}}\left( x+1 \right)\left( x+2 \right)x\left( x+3 \right).$

Do $g'\left( x \right)$ đổi dấu từ âm sang dương khi qua 3 điểm nên hàm số $g\left( x \right)$ có 3 điểm cực tiểu. Chọn C.
| Bài tập 8: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)=\left( {{x}^{2}}-3x+2 \right)\left( x-1 \right)$và $g\left( x \right)=-2f\left( 2-x \right)+{{x}^{2}}.$ Hàm số đạt cực trị tại điểm x bằng
A. $x=2.$ B. $x=-2.$ C. $x=-3.$ D. $x=3.$ |
Lời giải chi tiết
Ta có $f'\left( x \right)={{\left( x-1 \right)}^{2}}\left( x-2 \right)\xrightarrow{{}}f'\left( 2-x \right)=-x{{\left( 1-x \right)}^{2}}$
Lại có $g'\left( x \right)=2f\left( 2-x \right)+2x=-2x{{\left( 1-x \right)}^{2}}+2x=2{{x}^{2}}\left( 2-x \right).$
Phương trình $g'\left( x \right)=0\Leftrightarrow 2{{x}^{2}}\left( 2-x \right)=0\Leftrightarrow \left[ \begin{matrix} x=0 \\
x=2 \\\end{matrix}. \right.$
Suy ra hàm số đạt cực tiểu tại điểm ![]() Chọn A.
Chọn A.
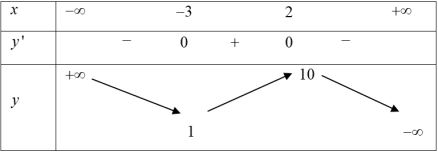
| Bài tập 9: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
Hàm số $y=\left( \sqrt{{{x}^{2}}+x+2} \right)$ có mấy điểm cực trị? A. 9. B. 7. C. 6. D. 5. |
Lời giải chi tiết
Ta có $y=\left( \sqrt{{{x}^{2}}+x+2} \right)\xrightarrow{{}}y'=\frac{2x-1}{2\sqrt{{{x}^{2}}+x+2}}.f'\left( \sqrt{{{x}^{2}}+x+2} \right).$
Xét $y'=0\Leftrightarrow \left( 2x+1 \right).f'\left( \sqrt{{{x}^{2}}+x+2} \right)=0\Leftrightarrow \left[ \begin{matrix} x=-\frac{1}{2}\text{ } \\ f'\left( \sqrt{{{x}^{2}}+x+2} \right)=0\text{ (*)} \\\end{matrix} \right.$
Lại có $f'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=\pm 1 \\ x=2\text{ } \\ x=4\text{ } \\ {} \\\end{matrix} \right.$ suy ra (*)$\Leftrightarrow \left[ \begin{matrix} \sqrt{{{x}^{2}}+x+2}=\pm 1 \\ \sqrt{{{x}^{2}}+x+2}=2\text{ } \\ \sqrt{{{x}^{2}}+x+2}=4\text{ } \\\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix} {{x}^{2}}+x+1=0 \\ {{x}^{2}}+x=2\text{ } \\ {{x}^{2}}+x=14\text{ } \\\end{matrix} \right.$ (có 4 nghiệm).
Suy ra hàm số đã cho có 5 điểm cực trị. Chọn D.
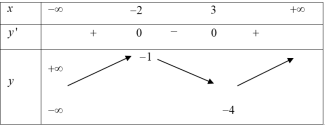
| Bài tập 10: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ dưới
Số điểm cực trị của hàm số $y=\left| f\left( 2x-1 \right) \right|$ là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Ta có: $y=\left| f\left( x \right) \right|$ thì $y'=\frac{f'\left( x \right).f\left( x \right)}{\left| f\left( x \right) \right|}$
Ta có: $y=\left| f\left( 2x-1 \right) \right|\Rightarrow y'=\frac{\left[ f\left( 2x-1 \right) \right]'.f\left( 2x-1 \right)}{\left| f\left( 2x-1 \right) \right|}=\frac{2f'\left( 2x-1 \right).f\left( 2x-1 \right)}{\left| f\left( 2x-1 \right) \right|}(*)$
Dựa vào BBT suy ra phương trình $f\left( x \right)=0$ có một nghiệm $x=a>2$ nên phương trình
$f\left( 2x-1 \right)=0\Leftrightarrow 2x-1=a(1)$có 1 nghiệm.
$f'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=-3 \\ x=2\text{ } \\\end{matrix} \right.\Rightarrow f\left( 2x-1 \right)=0\Leftrightarrow \left[ \begin{matrix} 2x-1=-3 \\ 2x-1=2\text{ } \\\end{matrix} \right.(2)$
Từ (1) và (2) suy ra phương trình (*) có 3 nghiệm phân biệt.
Vậy hàm số $y=\left| f\left( 2x-1 \right) \right|$ có 3 điểm cực trị. Chọn A.
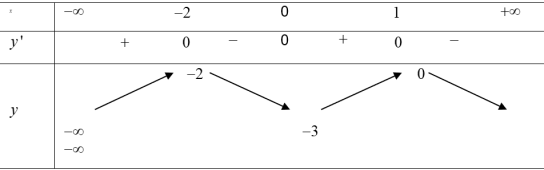
| Bài tập 11: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ dưới:
Số điểm cực trị của hàm số $y=\left| f\left( {{x}^{2}}+2 \right) \right|$ là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Ta có: $f'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=-2 \\ x=3\text{ } \\\end{matrix} \right.$
Ta có: $y=\left( \left| f\left( {{x}^{2}}+2 \right) \right| \right)\begin{matrix} ' \\ {} \\\end{matrix}=\frac{f\left( {{x}^{2}}+2 \right)\left[ f\left( {{x}^{2}}+2 \right) \right]'}{\left| f\left( {{x}^{2}}+2 \right) \right|}=\frac{f\left( {{x}^{2}}+2 \right).2x.f'\left( {{x}^{2}}+2 \right)}{\left| f\left( {{x}^{2}}+2 \right) \right|}(*)$
Dựa vào BBT ta có thể giả sử $f\left( x \right)=0$ có 1 nghiệm duy nhất là$x=a>3$
Khi đó $f\left( {{x}^{2}}+2 \right)=0\Leftrightarrow {{x}^{2}}+2=a(1)$
Mặt khác $2x.f'\left( {{x}^{2}}+2 \right)=0\Leftrightarrow \left[ \begin{matrix} x=0\text{ } \\ {{x}^{2}}+2=-2(2) \\ {{x}^{2}}+2=3\text{ } \\\end{matrix} \right.$
Từ (1) và (2) suy ra (*) có 5 nghiệm phân biệt suy ra hàm số $y=\left| f\left( {{x}^{2}}+2 \right) \right|$ có 5 điểm cực trị.
Chọn C.
| Bài tập 12: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{\left( x+1 \right)}^{2}}\left( {{x}^{2}}-3x \right),$với mọi $x\in \mathbb{R}$. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số$y=f\left( {{x}^{2}}-4x-m \right)$ có 5 điểm cực trị?
A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Ta có $g'\left( x \right)=\left( 2x-4 \right)f'\left( {{x}^{2}}-4x-m \right)=2\left( x-2 \right){{\left( t+1 \right)}^{2}}\left( {{t}^{2}}-3t \right)$ (với $t={{x}^{2}}-4x-m$)
Số điểm cực trị của hàm số $g\left( x \right)$ là số nghiệm bội lẻ của phương trình $\left( x-2 \right)\left( {{t}^{2}}-3t \right)=0$
$\Leftrightarrow \left( x-2 \right)\left( {{x}^{2}}-4x-m \right)\left( {{x}^{2}}-4x-m-3 \right)=0$
Hàm số có 5 điểm cực trị khi các phương trình $u\left( x \right)={{x}^{2}}-4m-m=0$ và $v\left( x \right)={{x}^{2}}-4m-m-3=0$
Có 2 nghiệm phân biệt khác nhau và khác 2 $\Leftrightarrow \left\{ \begin{matrix} \Delta _{u}^{'}=4+m>0\text{ } \\ \Delta _{u}^{'}=4+m+3>0 \\ u\left( 2 \right)=-4-m\ne 0 \\ v\left( 2 \right)=-7-m\ne 0 \\\end{matrix} \right.\Leftrightarrow m>-4$
Vậy 3 giá trị nguyên âm của m thỏa mãn yêu cầu. Chọn A.
| Bài tập 13: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{\left( x-2 \right)}^{4}}\left( {{x}^{3}}-x \right),$với mọi $x\in \mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m\in \left[ -10;0 \right]$ để hàm số$y=f\left( {{x}^{2}}+m \right)$ có 7 điểm cực trị?
A. 9. B. 7. C. 8. D. 10. |
Lời giải chi tiết
Ta có $g'\left( x \right)=\left[ f\left( {{x}^{2}}+m \right) \right]'=2x.f'\left( {{x}^{2}}+m \right)=2x{{\left( t-2 \right)}^{4}}\left( {{t}^{3}}-t \right)$ (với $t={{x}^{2}}+m$)
Số điểm cực trị của hàm số $g\left( x \right)$ là số nghiệm bội lẻ của phương trình $x.t\left( {{t}^{2}}-1 \right)$
$\Leftrightarrow x\left( {{x}^{2}}+m \right)\left( {{x}^{2}}+m-1 \right)\left( {{x}^{2}}+m+1 \right)=0\Leftrightarrow \left[ \begin{matrix} x=0\text{ } \\ {{x}^{2}}=-m\text{ } \\ {{x}^{2}}=1-m\text{ } \\ {{x}^{2}}=-1-m \\\end{matrix} \right.(*)$
PT (*) có 7 nghiệm phân biệt khi $\Leftrightarrow \left\{ \begin{matrix} -m>0\text{ } \\ 1-m>0\text{ } \\ -1-m>0 \\\end{matrix} \right.\Leftrightarrow m<-1.$
Vậy có 8 giá trị nguyên âm của $m\in \left[ -10;0 \right]$ thỏa mãn. Chọn C.
| Bài tập 14: Cho hàm số $y=f\left( x \right)$ liên tục trên khoảng $\mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây
Số giá trị nguyên của tham số $m\in \left[ -10;10 \right]$ để hàm số$g\left( x \right)={{\left[ f\left( x \right)+m \right]}^{2}}$ có 5 điểm cực trị là: A. 11. B. 10. C. 9. D. 12. |
Lời giải chi tiết
Ta có: $g'\left( x \right)=2.f'\left( x \right).\left[ f\left( x \right)+m \right]=0\Leftrightarrow \left[ \begin{matrix} f'\left( x \right)=0\text{ } \\ f\left( x \right)=-m \\\end{matrix} \right.$
Do hàm số $y=f\left( x \right)$ có 3 điểm cực trị nên phương trình $f'\left( x \right)=0$ có 3 nghiệm phân biệt.
Để hàm số$g\left( x \right)$ có 5 điểm cực trị thì phương trình $f\left( x \right)=-m$ có 2 nghiệm phân biệt
$\Leftrightarrow \left[ \begin{matrix} -2\le m<0 \\ m\le -3\text{ } \\\end{matrix} \right.$
Chú ý:Với $m=-2,m=-3$ thì $f'\left( x \right)=-m$ có nghiệm kép tại $x=-2.$
Kết hợp với $m\in \mathbb{Z}\Rightarrow m=\left\{ -10;-8;-7;-6;-5;-4;-3;-2;-1 \right\}.$ Chọn B.
| Bài tập 15: Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)=\left( {{x}^{3}}-2{{x}^{2}} \right)\left( {{x}^{3}}-2x \right),$với mọi $x\in \mathbb{R}$. Hàm số$y=\left| f\left( 1-2018x \right) \right|$ có nhiều nhất bao nhiêu điểm cực trị?
A. 9. B. 2018. C. 2022. D. 11. |
Lời giải chi tiết
Ta có $f'\left( x \right)=\left( {{x}^{3}}-2{{x}^{2}} \right)\left( {{x}^{3}}-2x \right)={{x}^{3}}\left( x-2 \right)\left( {{x}^{2}}-2 \right);\forall x\in \mathbb{R}.$
Số điểm cực trị của hàm số $y=g\left( x \right)=\left| f\left( 1-2018x \right) \right|$ là tổng số nghiệm của phương trình
$g'\left( x \right)=0\Leftrightarrow 2018.f'\left( 1-2018x \right)=0\xrightarrow{{}}$ có 4 điểm.
Số nghiệm của phương trình $\left( 1-2018x \right)=0\xrightarrow{{}}$ có tối đa 5 nghiệm vì đạo hàm có 4 nghiệm.
Vậy hàm số đã cho có tối đa 9 điểm cực trị. Chọn A.
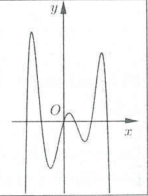
| Bài tập 16: Hàm số đa thức bậc sáu $y=f\left( x \right)$ có đồ thị như hình vẽ bên cạnh.
Hàm số $g\left( x \right)=f\left( 3-\sqrt{3}x \right)$ có bao nhiêu điểm cực trị? A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Số điểm cực trị của hàm số $y=f\left( ax+b \right)$ bằng số điểm cực trị của hàm số $y=f\left( x \right)$
Dựa vào hình vẽ, ta thấy hàm số $y=f\left( x \right)$ có 5 điểm cực trị.
Chọn C.
| Bài tập 13: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu như hình vẽ.
Gọi m, n lần lượt là số điểm cực đại, số điểm cực tiểu của hàm số. Tính ${{m}^{2}}-2n.$ A. 3. B. 6. C.$-1$. D. 0. |
Lời giải chi tiết
Ta thấy $f'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix} x=-1 \\ x=2\text{ } \\ x=4\text{ } \\\end{matrix} \right.$ và $f'\left( x \right)$ không xác định tại $x=0.$
TOÁN LỚP 12