Bài tập Tiếp tuyến với bài toán tương giao có đáp án chi tiết

Bài tập Tiếp tuyến với bài toán tương giao có đáp án

Phương pháp giải bài toán tiếp tuyến với bài toán tương giao

Viết phương trình hoành độ giữa đồ thị hàm số $y=f\left( x \right)\left( C \right)$ và đường thẳng $d:y=ax+b$. Gọi $A\left( {{x}_{i}};a{{x}_{i}}+b \right)$ là tọa độ giao điểm khi đó ${{k}_{i}}={f}'\left( {{x}_{i}} \right)$ là hệ số góc của tiếp tuyến của $\left( C \right)$ tại điểm A.

Bài tập trắc nghiệm tiếp tuyến và tương giao có đáp án chi tiết

Lời giải

Phương trình hoành độ giao điểm là: $\frac{-x+1}{2\text{x}-1}=x+m\Leftrightarrow \left( x+m \right)\left( 2\text{x}-1 \right)=-x+1$ (Do $x=\frac{1}{2}$ không phải là nghiệm) $\Leftrightarrow 2{{\text{x}}^{2}}+2\text{x}-m-1=0\left( * \right)$.

Ta có: ${\Delta }'={{m}^{2}}+2m+2>0\left( \forall x\in \mathbb{R} \right)\Rightarrow d$ luôn cắt $\left( C \right)$ tại 2 điểm phân biệt.

Gọi ${{x}_{1}},{{x}_{2}}$ là nghiệm của phương trình (*) theo định lý Vi-ét ta có: $\left\{ \begin{array}  {} {{x}_{1}}+{{x}_{2}}=-1 \\  {} {{x}_{1}}{{x}_{2}}=\frac{-m-1}{2} \\ \end{array} \right.$

Khi đó ${{k}_{1}}+{{x}_{2}}=\frac{-1}{{{\left( 2{{\text{x}}_{1}}-1 \right)}^{2}}}-\frac{1}{{{\left( 2{{\text{x}}_{2}}-1 \right)}^{2}}}=-\frac{4{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-8{{\text{x}}_{1}}{{x}_{2}}-4\left( {{x}_{1}}+{{x}_{2}} \right)+2}{{{\left[ 4{{\text{x}}_{1}}{{x}_{2}}-2\left( {{x}_{1}}+{{x}_{2}} \right)+1 \right]}^{2}}}$

$=-4{{m}^{2}}-8m-6=-4{{\left( m+1 \right)}^{2}}-2\le -2$.

Do đó ${{k}_{1}}+{{k}_{2}}$ đạt giá trị lớn nhất $\Leftrightarrow m=-1$.

Lời giải

Phương trình đường thẳng d là: $y=k\text{x}+3$

Phương trình hoành độ giao điểm là: ${{x}^{3}}+4{{\text{x}}^{2}}+3=k\text{x}+3\Leftrightarrow \left[ \begin{array}  {} {{x}_{3}}=0\Rightarrow A\left( 0;3 \right) \\  {} g\left( x \right)={{x}^{2}}+4\text{x}-k=0 \\ \end{array} \right.$

Để d cắt $\left( C \right)$ tại 3 điểm phân biệt $\Leftrightarrow g\left( x \right)=0$ có 2 nghiệm phân biệt khác 0

$\Leftrightarrow \left\{ \begin{array}  {} {\Delta }'=4+k>0 \\  {} k\ne 0 \\ \end{array} \right.\Leftrightarrow 0\ne k>-4$

Khi đó gọi, $B\left( {{x}_{1}};k{{\text{x}}_{1}}+3 \right)$, $C\left( {{x}_{2}};k{{x}_{2}}+3 \right)$$\Rightarrow {{k}_{1}}={y}'\left( {{x}_{1}} \right)=3\text{x}_{1}^{2}+8{{\text{x}}_{1}},{{k}_{2}}=3\text{x}_{2}^{2}+8{{\text{x}}_{2}}$

Để các tiếp tuyến tại B, C vuông góc với nhau $\Leftrightarrow {{k}_{1}}.{{k}_{2}}=-1$

$\Leftrightarrow {{x}_{1}}.{{x}_{2}}\left( 3{{\text{x}}_{1}}+8 \right)\left( 3{{\text{x}}_{2}}+8 \right)=-1\Leftrightarrow {{x}_{1}}.{{x}_{2}}\left( 9{{\text{x}}_{1}}{{x}_{2}}+24\left( {{x}_{1}}+{{x}_{2}} \right)+64 \right)=-1$

$\Leftrightarrow -k\left( -9k-32 \right)=-1\Leftrightarrow 9{{k}^{2}}+32k+1=0\Leftrightarrow k=\frac{-16\pm \sqrt{247}}{9}$ (thỏa mãn)

Vậy $k=\frac{-16\pm \sqrt{247}}{9}\Rightarrow d_y=\frac{-16\pm \sqrt{247}}{9}x+3$.

Lời giải

Phương trình hoành độ giao điểm là $\frac{x-1}{x-2}=2\text{x}+1\Leftrightarrow \left\{ \begin{array}  {} x\ne 2 \\  {} 2{{\text{x}}^{2}}-4\text{x}-1=0 \\ \end{array} \right.\Leftrightarrow x=\frac{2\pm \sqrt{6}}{2}$

Mặt khác ta có: ${y}'=\frac{-1}{{{\left( x-2 \right)}^{2}}}\Rightarrow {{k}_{1}}+{{k}_{2}}={y}'\left( \frac{2+\sqrt{6}}{2} \right)+{y}'\left( \frac{2-\sqrt{6}}{2} \right)=20$. Chọn C.

Lời giải

Phương trình hoành độ giao điểm là ${{x}^{2}}-2m\text{x}+1=0$

Đk cắt tại 2 điểm phân biệt là: ${\Delta }'={{m}^{2}}-1>0$. Khi đó ${{x}_{1}};{{x}_{2}}$ là hoành độ giao điểm thì $\left\{ \begin{array}  {} {{x}_{1}}+{{x}_{2}}=2m \\  {} {{x}_{1}}{{x}_{2}}=1 \\ \end{array} \right.$

Lại có ${y}'=2\text{x}-2\Rightarrow {y}'\left( {{x}_{1}} \right)+{y}'\left( {{x}_{2}} \right)=2{{\text{x}}_{1}}-2+2{{\text{x}}_{2}}-2=4m-4=4\Leftrightarrow m=2$. Chọn A.

Lời giải

Phương trình hoành độ giao điểm là: ${{x}^{3}}-3\left( m+1 \right){{x}^{2}}+3m\text{x}+2=0$

$\Leftrightarrow \left( x-1 \right)\left( {{x}^{2}}-\left( 3m+2 \right)x-2 \right)=0\Leftrightarrow \left\{ \begin{array}  {} x=1 \\  {} g\left( x \right)={{x}^{2}}-\left( 3m+2 \right)x-2=0 \\ \end{array} \right.$

+) Để $\left( C \right)$ cắt Ox tại 3 điểm phân biệt $\Leftrightarrow g\left( x \right)=0$ có 2 nghiệm phân biệt khác 1.

$\Leftrightarrow \left\{ \begin{array}  {} \Delta ={{\left( 3m+2 \right)}^{2}}+8>0 \\  {} g\left( 1 \right)=-3m-3\ne 0 \\ \end{array} \right.\left( * \right)$

Khi đó gọi, $B\left( {{x}_{1}};0 \right),C\left( {{x}_{2}};0 \right)\Rightarrow \left\{ \begin{array}  {} {{x}_{1}}+{{x}_{2}}=3m+2 \\  {} {{x}_{1}}{{x}_{2}}=-2 \\ \end{array} \right.\left( {{x}_{1}}\ne {{x}_{2}} \right)$

Ta có: ${{k}_{1}}={y}'\left( {{x}_{1}} \right)=3\text{x}_{1}^{2}-6\left( m+1 \right){{x}_{1}}+3m,{{k}_{2}}={y}'\left( {{x}_{2}} \right)=3x_{2}^{2}-6\left( m+1 \right){{x}_{2}}+3m$

Do tiếp tuyến tại B và C song song nên ta có: ${{k}_{1}}={{k}_{2}}\Leftrightarrow x_{1}^{2}-2\left( m+1 \right){{x}_{1}}=x_{2}^{2}-2\left( m+1 \right){{x}_{2}}$

$\Leftrightarrow \left( {{x}_{1}}-{{x}_{2}} \right)\left( {{x}_{1}}+{{x}_{2}}-2m-2 \right)=0\Leftrightarrow {{x}_{1}}+{{x}_{2}}=2m+2\Leftrightarrow 3m+2=2m+2\Leftrightarrow m=0$ (t/m). Chọn A.

Lời giải

Từ giả thiết ta được đường thẳng MN có một vectơ chỉ phương $\overrightarrow{u}\left( 1;6 \right)$.

Suy ra hệ số góc của đường thẳng MN bằng 6.

Gọi $A\left( {{x}_{0}};{{y}_{0}} \right)$ ta có: ${f}'\left( {{x}_{0}} \right)=6\Leftrightarrow x_{0}^{3}-7{{\text{x}}_{0}}=6\Leftrightarrow \left[ \begin{array}  {} {{x}_{0}}=3 \\  {} {{x}_{0}}=-1 \\  {} {{x}_{0}}=-2 \\ \end{array} \right.$.

Ta được các phương trình tiếp tuyến tương ứng là $y=6x-\frac{117}{4}$, $y=6\text{x}+\frac{11}{4}$, $y=6\text{x}+2$.

Kiểm tra điều kiện cắt tại 3 điểm

Ta xét phương trình $\frac{1}{4}{{x}^{4}}-\frac{7}{2}{{x}^{2}}=6\text{x}+m\Leftrightarrow g\left( x \right)=\frac{1}{4}{{x}^{4}}-\frac{7}{2}{{x}^{2}}-6\text{x}=m\left( * \right)$.

Khi đó ${g}'\left( x \right)=0\Leftrightarrow {{x}^{3}}-7\text{x}-6=0\Leftrightarrow \left[ \begin{array}  {} x=3 \\  {} x=-1 \\  {} x=-2 \\ \end{array} \right.$. Ta được bảng biến thiên sau:

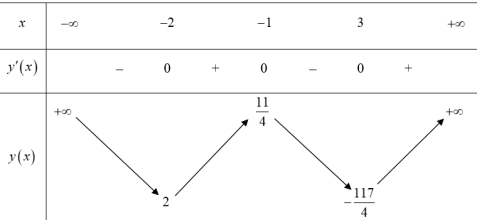
Dựa vào BBT suy ra $m=\frac{11}{4}$, $m=2$ thì phương trình (*) có ba nghiệm.

Vậy có hai điểm A thỏa mãn yêu cầu bài toán. Chọn B.

Lời giải

Ta có ${y}'\left( {{x}_{1}} \right)={y}'\left( {{x}_{2}} \right)=5\Leftrightarrow \left[ \begin{array}  {} 3\text{x}_{1}^{2}+6m{{\text{x}}_{1}}+2=5 \\  {} 3\text{x}_{2}^{2}+6m{{\text{x}}_{1}}+2=5 \\ \end{array} \right.$. Khi đó ${{x}_{1}};{{x}_{2}}$ là nghiệm của phương trình

$3{{\text{x}}^{2}}+6m\text{x}+2=5$ hay ${{x}^{2}}+2m\text{x}-1=0\left( {{m}^{2}}+1>0 \right)$. Theo Vi-ét ta có: $\left\{ \begin{array}  {} {{x}_{1}}+{{x}_{2}}=-2m \\  {} {{x}_{1}}{{x}_{2}}=-1 \\ \end{array} \right.$

Lại có $x_{1}^{2}+x_{2}^{2}={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{\text{x}}_{1}}{{x}_{2}}=4{{m}^{2}}+2=10\Leftrightarrow m=\pm \sqrt{2}$. Chọn B.

Lời giải

Viết lại $d:y=\frac{1}{3}x+\frac{2}{3}$. ${y}'=3{{\text{x}}^{2}}-6m\text{x}+3\left( m+1 \right)$

Ta có: ${y}'\left( {{x}_{1}} \right).\frac{1}{3}=-1$, ${y}'\left( {{x}_{2}} \right).\frac{1}{3}=-1$ nên ${{x}_{1}};{{x}_{2}}$ là nghiệm của PT: ${{x}^{2}}-2m\text{x}+m+1=-1$

$\Leftrightarrow {{x}^{2}}-2m\text{x}+m+2=0\left( 1 \right)$

Để tồn tại 2 điểm M, N thỏa mãn yêu cầu bài toán thì phương trình (1) có 2 nghiệm phân biệt dương

$\Leftrightarrow \left\{ \begin{array}  {} {\Delta }'={{m}^{2}}-m-2>0 \\  {} 2m>0 \\  {} m+2>0 \\ \end{array} \right.\Leftrightarrow m>2$.

Khi đó ta có: $\left\{ \begin{array}  {} {{x}_{1}}+{{x}_{2}}=2m \\  {} {{x}_{1}}{{x}_{2}}=m+2 \\ \end{array} \right.\Rightarrow {{\left( \sqrt{{{x}_{1}}}+\sqrt{{{x}_{2}}} \right)}^{2}}={{x}_{1}}+{{x}_{2}}+2\sqrt{{{x}_{1}}{{x}_{2}}}=2m+2\sqrt{m+2}=20$

$\Leftrightarrow \left\{ \begin{array}  {} m<10 \\  {} m+2={{\left( 10-m \right)}^{2}} \\  \end{array} \right.\Leftrightarrow m=7$ (tm). Chọn A.