Bài tập thể tích Hình trụ nội - ngoại tiếp hình lăng trụ đứng

Bài tập thể tích Hình trụ nội - ngoại tiếp hình lăng trụ đứng

Phương pháp: Hình trụ nội - ngoại tiếp lăng trụ đứng có chiều cao bằng độ dài cạnh bên của lăng trụ và đáy là đường tròn nội - ngoại tiếp đa giác đáy của lăng trụ (tham khảo hình vẽ)

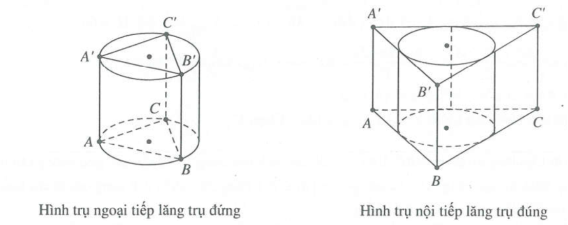
Dưới dây là một số bài tập trắc nghiệm hình trụ nội tiếp, ngoại tiếp lăng trụ hay ra trong đề thi có đáp án chi tiết

Lời giải chi tiết

• Chiều cao của khối trụ là $h=A{A}'=4$

• Bán kính đường tròn ngoại tiếp ΔABC là ${{R}_{\Delta ABC}}=\frac{{{2}^{2}}.\sqrt{3}}{4}=\sqrt{3}$

Suy ra bán kính đáy hình trụ là $R=\sqrt{3}.$ Vậy thể tích khối trụ là $V=\pi {{R}^{2}}h=12\pi .$ Chọn D.

Lời giải chi tiết

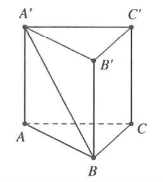
Tam giác ABC vuông tại A, có $BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=2a$

Suy ra bán kính đường tròn ngoại tiếp ΔABC là ${{R}_{\Delta ABC}}=\frac{BC}{2}=a$

Ta có $A{A}'\bot \left( ABC \right)\Rightarrow \widehat{{A}'B;\left( ABC \right)}=\widehat{\left( A{A}';AB \right)}=\widehat{{A}'BA}={{60}^{0}}$

Tam giác A'AB vuông tại A, có $A{A}'=AB.\tan {{60}^{\circ }}=a\sqrt{3}$

Khối trụ ngoại tiếp lăng trụ có $h=A{A}'=a\sqrt{3};R={{R}_{\Delta ABC}}=a$

Vậy thể tích khối trụ là $V=\pi {{R}^{2}}h=\sqrt{3}\pi {{a}^{3}}.$ Chọn B.

Lời giải chi tiết

Thể tích khối trụ là $V=2\pi {{a}^{3}}=\pi {{R}^{2}}h\xrightarrow{{}}{{R}^{2}}h=2{{a}^{3}},$với $\left\{ \begin{array}  {} R={{r}_{\Delta ABC}} \\  {} h=A{A}' \\ \end{array} \right.$

Tam giác ABC vuông tại A, có $AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=4a\Rightarrow {{S}_{_{\Delta ABC}}}=\frac{1}{2}.AB.AC=6{{a}^{2}}$

Ta có $p=\frac{AB+BC+AC}{2}=\frac{3a+4a+5a}{2}=6a\xrightarrow{{}}{{r}_{\Delta ABC}}=\frac{S}{p}=6{{a}^{2}}:6a=a$

Do đó $R=a\Rightarrow {{a}^{2}}h=2{{a}^{3}}\Rightarrow h=A{A}'=2a.$

Vậy thể tích khối lăng trụ là $V=A{A}'.{{S}_{_{\Delta ABC}}}=12{{a}^{3}}.$ Chọn C.

Lời giải chi tiết

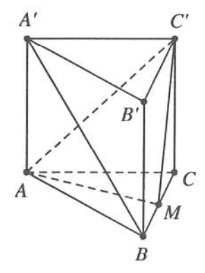
Gọi M là trung điểm $BC\Rightarrow AM\bot BC$ mà $B{B}'\bot AM$

Suy ra $AM\bot \left( BC{C}'{B}' \right)\Rightarrow \widehat{A{C}';\left( BC{C}'{B}' \right)}=\widehat{A{C}'M}={{30}^{0}}$

Đặt $AB=AC=x\xrightarrow{{}}BC=x\sqrt{2}\Rightarrow AM=\frac{x\sqrt{2}}{2};A{C}'=\sqrt{{{x}^{2}}+{{a}^{2}}}$

Tam giác AC'M vuông tại M, có $\sin \widehat{A{C}'M}=\frac{AM}{A{C}'}\Leftrightarrow A{C}'=2AM$

$\Leftrightarrow {{x}^{2}}+{{a}^{2}}=4.{{\left( \frac{x\sqrt{2}}{2} \right)}^{2}}\Leftrightarrow x=a\xrightarrow{{}}{{R}_{\Delta ABC}}=\frac{BC}{2}=\frac{a\sqrt{2}}{2}$

Vậy diện tích xung quanh khối trụ là ${{S}_{xq}}=2\pi Rh=\sqrt{2}\pi {{a}^{2}}.$ Chọn A.

Lời giải chi tiết

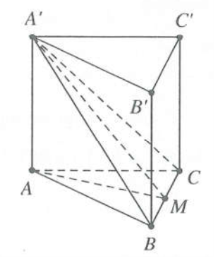
Dựng $AM\bot BC$ mà $A{A}'\bot BC\Rightarrow BC\bot \left( {A}'AM \right)$

Do đó $\widehat{\left( {A}'BC \right);\left( ABC \right)}=\widehat{{A}'MA}={{30}^{0}}$ mà $AM=\frac{AB\sqrt{3}}{2}=\frac{3\text{a}}{2}.$

Suy ra $A{A}'=AM.tan\widehat{{A}'MA}=\frac{3\text{a}}{2}.tan{{30}^{0}}=\frac{a\sqrt{3}}{2}$

Bán kính đường tròn nội tiếp ΔABC là ${{r}_{\Delta ABC}}=\frac{AB\sqrt{3}}{6}=\frac{\text{a}}{2}$

Khối trụ nội tiếp lăng trụ ABC.A'B'C' có $\left\{ \begin{array}  {} R={{r}_{\Delta ABC}}=\frac{a}{2} \\  {} h=A{A}'=\frac{a\sqrt{3}}{2} \\ \end{array} \right.$

Vậy thể tích khối trụ là $V=\pi {{R}^{2}}h=\pi .{{\left( \frac{a}{2} \right)}^{2}}.\frac{a\sqrt{3}}{2}=\frac{\sqrt{3}\pi {{a}^{3}}}{8}.$ Chọn D.

Lời giải chi tiết

Chiều cao của hình trụ là $h=A{A}'=a$

Hình lập phương có đáy là hình vuông $\xrightarrow[{}]{}{{R}_{\Delta ABC}}=\frac{AC}{2}=\frac{a\sqrt{2}}{2}$

Suy ra bán kính đáy hình trụ là $R=\frac{a\sqrt{2}}{2}\Rightarrow {{S}_{xq}}=2\pi Rh=\sqrt{2}\pi {{a}^{2}}.$ Chọn B.

Lời giải chi tiết

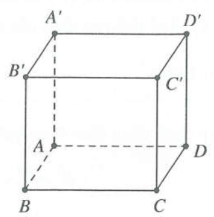
Ta có $\left\{ \begin{array}  {} CD\bot D{D}' \\  {} CD\bot AD \\ \end{array} \right.\Rightarrow CD\bot \left( AD{D}'{A}' \right)\Rightarrow CD\bot {A}'D$

Suy ra ${{S}_{\Delta {A}'C\text{D}}}=\frac{1}{2}.{A}'D.C\text{D}=\frac{{{a}^{2}}\sqrt{13}}{2}\xrightarrow{{}}{A}'D=a\sqrt{13}$

Do đó $A{A}'=\sqrt{{A}'{{D}^{2}}-A{{D}^{2}}}=\sqrt{{{\left( a\sqrt{13} \right)}^{2}}-{{\left( 2a \right)}^{2}}}=3a$

Khối trụ ngoại tiếp hình hộp chữ nhật có $\left\{ \begin{array}  {} R=\frac{AC}{2}=\frac{a\sqrt{5}}{2} \\  {} h=A{A}'=3a \\ \end{array} \right.$

Thế tích khối trụ cần tính là $V=\pi {{R}^{2}}h=\pi .{{\left( \frac{a\sqrt{5}}{2} \right)}^{2}}.3a=\frac{15\pi {{a}^{3}}}{4}.$ Chọn C.

Lời giải chi tiết

Gọi O là tâm hình vuông $ABCD\Rightarrow BD\bot AO\Rightarrow BD\bot \left( {A}'AO \right)$

Khi đó $\widehat{\left( {A}'BD \right);\left( ABCD \right)}=\widehat{\left( {A}'O;OA \right)}=\widehat{{A}'OA}={{45}^{0}}$

Suy ra tam giác A'AO vuông cân tại $A\xrightarrow{{}}A{A}'=OA=\frac{a\sqrt{2}}{2}$

Bán kính đường tròn nội tiếp hình vuông ABCD là ${{r}_{\Delta ABC}}=\frac{a}{2}$

Khối trụ nội tiếp lăng trụ đứng có $R={{r}_{\Delta ABC}}=\frac{a}{2};h=A{A}'=\frac{a\sqrt{2}}{2}$

Vậy diện tích xung quanh cần tính là ${{S}_{xq}}=2\pi Rh=\frac{\sqrt{2}\pi {{a}^{2}}}{2}.$ Chọn D.