Bài tập phản ứng hạt nhân các định luật bảo toàn có đáp án chi tiết

CÁC DẠNG BÀI CHUYÊN ĐỀ PHẢN ỨNG HẠT NHÂN

DẠNG 1: VIẾT PHƯƠNG TRÌNH PHẢN ỨNG HẠT NHÂN.

PHƯƠNG PHÁP GIẢI

Phương trình phản ứng hạt nhân: ${}_{Z1}^{A1}A+{}_{Z2}^{A2}B\to {}_{Z3}^{A3}X+{}_{Z4}^{A4}Y$

Xác định tên của các hạt nhân bằng cách dựa vào hai định luật bảo toàn điện tích và bảo toàn số khối: $\left\{ \begin{array}{} {{A}_{1}}+{{A}_{2}}={{A}_{3}}+{{A}_{4}} \\ {} {{Z}_{1}}+{{Z}_{2}}={{Z}_{3}}+{{Z}_{4}} \\ \end{array} \right.$.

BÀI TẬP LUYỆN TẬP DẠNG 1

Lời giải chi tiết:

Phương trình phản ứng hạt nhân: ${}_{1}^{1}p+{}_{4}^{9}Be\xrightarrow{{}}{}_{2}^{4}He+{}_{Z}^{A}X$

Áp dụng định luật bảo toàn điện tích: $1+4=2+Z\Rightarrow Z=3$

Áp dụng định luật bảo toàn số khối: $1+9=4+A\Rightarrow A=6$

Vậy hạt nhân X có kí hiệu là ${}_{3}^{6}X$, và X là hạt nhân ${}_{3}^{6}Li$

Hạt nhân X có 3 prôtôn và $(6-3)=3$ nơtrôn. Chọn A.

Lời giải chi tiết:

Bảo toàn điện tích: $Z=Z+1+{{Z}_{X}}\Rightarrow {{Z}_{X}}=1$

Bảo toàn số khối: $A=A+{{A}_{X}}\Rightarrow {{A}_{X}}=0\Rightarrow X={}_{1}^{0}{{\beta }^{+}}$. Chọn C.

Lời giải chi tiết:

Bảo toàn điện tích và số khối, ta được hệ phương trình:

$\left\{ \begin{array}{} 4x+0.y=238-206=32 \\ {} 2x+(-1).y=92-82=10 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} x=8 \\ {} 2x-y=10 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} x=8 \\ {} y=6 \\ \end{array} \right.$. Chọn C.

Lời giải chi tiết:

Điện tích và số khối của các tia và hạt còn lại trong phản ứng: ${}_{0}^{1}n;{}_{-1}^{0}\beta $.

Phương trình phản ứng là: ${}_{0}^{1}n+{}_{92}^{235}U\xrightarrow{{}}{}_{42}^{95}Mo+{}_{57}^{139}La+2X+7{}_{-1}^{0}{{\beta }^{-}}$

Áp dụng định luật bảo toàn điện tích và số khối ta được: 2 hạt X có

$\left\{ \begin{array}{} 2Z=0+92-42-57-7(-1)=0 \\ {} 2A=1+235-95-139-7.0=2 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} Z=0 \\ {} Z=1 \\ \end{array} \right.\Rightarrow X\text{ }$là $_{0}^{1}n$ Chọn D.

Lời giải chi tiết:

Phương trình phản ứng: ${}_{90}^{232}Th\xrightarrow{{}}{}_{82}^{208}Pb+x{}_{2}^{4}He+y{}_{-1}^{0}\beta $

Áp dụng định luật bảo toàn điện tích và số khối, ta được:

$\left\{ \begin{array}{} 4x+0.y=232-208=24 \\ {} 2x+(-1).y=90-82=8 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} x=6 \\ {} 2x-y=8 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} x=6 \\ {} y=4 \\ \end{array} \right.$.

Vậy có 6 hạt $\alpha $ và 4 hạt ${{\beta }^{-}}$. Chọn D.

DẠNG 2: NĂNG LƯỢNG CỦA PHẢN ỨNG HẠT NHÂN.

PHƯƠNG PHÁP GIẢI

Phương trình phản ứng hạt nhân: ${}_{Z1}^{A1}A+{}_{Z2}^{A2}B\to {}_{Z3}^{A3}X+{}_{Z4}^{A4}Y$

Năng lượng của phản ứng hạt nhân:

$\Delta E=({{m}_{0}}-m).{{c}^{2}}$

$\Delta E=(\Delta m-\Delta {{m}_{0}}).{{c}^{2}}=\left[ (\Delta {{m}_{3}}+\Delta {{m}_{4}})-(\Delta {{m}_{1}}+\Delta {{m}_{2}}) \right]{{c}^{2}}$

$\Delta E=\Delta {{E}_{1k}}-\Delta {{E}_{1k0}}=(\Delta {{E}_{\ell k3}}+\Delta {{E}_{\ell k4}})-(\Delta {{E}_{\ell k1}}+\Delta {{E}_{\ell k2}})=({{A}_{3}}.{{\varepsilon }_{3}}+{{A}_{4}}.{{\varepsilon }_{4}})-({{A}_{1}}.{{\varepsilon }_{1}}+{{A}_{2}}.{{\varepsilon }_{2}})$

$\Delta E=K-{{K}_{0}}=({{K}_{3}}+{{K}_{4}})-({{K}_{1}}+{{K}_{2}})$.

+) Nếu $\Delta E>0\Rightarrow $phản ứng tỏa năng lượng.

+) Nếu $\Delta E<0\Rightarrow $phản ứng thu năng lượng.

BÀI TẬP LUYỆN TẬP DẠNG 2

Lời giải chi tiết:

Phương trình phản ứng: ${}_{4}^{9}Be+\alpha \xrightarrow{{}}{}_{6}^{12}C+n$

Năng lượng của phản ứng: $\Delta E=({{m}_{Be}}+{{m}_{\alpha }}-{{m}_{C}}-{{m}_{n}}){{c}^{2}}$

$\Leftrightarrow \Delta E=(9,0122+4,0015-12,0000-1,0087).931,5$

$\Leftrightarrow \Delta E\approx 4,66MeV>0\Rightarrow $ phản ứng hạt nhân này tỏa năng lượng. Chọn B.

Lời giải chi tiết:

Phương trình phản ứng: ${}_{13}^{27}Al+\alpha \xrightarrow{{}}{}_{15}^{30}P+n$

Năng lượng của phản ứng: $\Delta E=({{m}_{Al}}+{{m}_{\alpha }}-{{m}_{P}}-{{m}_{n}}){{c}^{2}}$

$\Leftrightarrow \Delta E=(26,9743+4,0016-29,9701-1,0087).931,5$

$\Leftrightarrow \Delta E=-2,7MeV<0\Rightarrow $ phản ứng hạt nhân này thu năng lượng. Chọn A.

Lời giải chi tiết:

Bảo toàn điện tích, số khối $\Rightarrow $ được phương trình của phản ứng và X cũng là ${}_{2}^{4}He$:

${}_{1}^{1}H+{}_{3}^{7}Li\xrightarrow{{}}{}_{2}^{4}He+X$

Vì vậy, cứ mỗi phản ứng hạt nhân có 2 hạt ${}_{2}^{4}He$ tạo thành. Do đó, số phản ứng hạt nhân bằng một nửa số hạt ${}_{2}^{4}He$ tạo thành.

Số hạt ${}_{2}^{4}He$ tạo thành là: ${{N}_{\frac{4}{2}He}}=n.{{N}_{A}}=0,5.6,{{02.10}^{23}}=3,{{01.10}^{23}}$ hạt

$\Rightarrow $ Cần có $N=\frac{1}{2}{{N}_{\frac{4}{2}He}}=\frac{1}{2}.3,{{01.10}^{23}}=1,{{505.10}^{23}}$ phản ứng.

Năng lượng tỏa ra là: $Q=N.\Delta E=1,{{505.10}^{23}}.17,3\approx 2,{{6.10}^{24}}MeV$. Chọn A.

Lời giải chi tiết:

Bảo toàn điện tích và số khối, suy ra được phương trình phản ứng và X là nơtrôn:

${}_{1}^{3}T+{}_{1}^{2}D\xrightarrow{{}}{}_{2}^{4}He+{}_{0}^{1}n$.

Năng lượng của phản ứng: $\Delta E=(\Delta {{m}_{He}}-\Delta {{m}_{D}}-\Delta {{m}_{T}}){{c}^{2}}$

$\Leftrightarrow \Delta E=(0,030382-0,002491-0,009106).931,5\Leftrightarrow \Delta E=17,498MeV$. Chọn C.

Lời giải chi tiết:

Phương trình phản ứng: ${}_{92}^{235}U+n\xrightarrow{{}}{}_{38}^{94}Sr+{}_{54}^{140}Xe+2n$

Năng lượng của phản ứng: $\Delta E={{A}_{Sr}}.{{\varepsilon }_{Sr}}+{{A}_{Xe}}.{{\varepsilon }_{Xe}}-{{A}_{U}}.{{\varepsilon }_{U}}$

$\Leftrightarrow \Delta E=94.8,59+140.8,29-235.7,59\Leftrightarrow \Delta E=184,4MeV$. Chọn D.

Lời giải chi tiết:

Phương trình phản ứng: ${}_{13}^{27}Al+\alpha \xrightarrow{{}}{}_{15}^{30}P+n$

Năng lượng của phản ứng: $\Delta E={{A}_{p}}.{{\varepsilon }_{p}}-\Delta {{E}_{Al}}-\Delta {{m}_{\alpha }}.{{c}^{2}}$

$\Leftrightarrow \Delta E=30.8,35-225,05-0,030382.931,5$

$\Leftrightarrow \Delta E\approx -2,85MeV<0\Rightarrow $ phản ứng thu năng lượng. Chọn A.

Lời giải chi tiết:

Phương trình phản ứng: ${}_{84}^{210}Po\xrightarrow{{}}{}_{2}^{4}\alpha +{}_{82}^{206}Pb+hf$

Năng lượng của bức xạ phát ra:

$hf=6,{{625.10}^{-34}}.3,{{07417.10}^{19}}=20,{{3664.10}^{-15}}J=0,12729MeV$

Ta có: $({{m}_{Po}}-{{m}_{Pb}}-{{m}_{\alpha }}){{c}^{2}}=\Delta E+{{K}_{\alpha }}+hf$

$\Leftrightarrow ({{m}_{Po}}-{{m}_{Pb}}-{{m}_{\alpha }}){{c}^{2}}=6,42735+6,18+0,12729=12,73464MeV=0,01367u{{c}^{2}}$

$\Rightarrow {{m}_{Pb}}={{m}_{Po}}-{{m}_{\alpha }}-0,01367u=209,9828u-4,0015u-0,01367u=205,96763u$. Chọn C.

Lời giải chi tiết:

Phương trình phản ứng: $\gamma +{}_{6}^{12}C\xrightarrow{{}}{}_{2}^{4}He+{}_{2}^{4}He+{}_{2}^{4}He$

Bảo toàn năng lượng toàn phần: $hf+{{m}_{C}}{{c}^{2}}=3{{m}_{He}}{{c}^{2}}+3{{K}_{\alpha }}$

Có: $hf=6,{{625.10}^{-34}}{{.4.10}^{21}}=2,{{65.10}^{-12}}J=16,5625MeV$

$\Rightarrow {{K}_{\alpha }}=\frac{hf+{{m}_{C}}{{c}^{2}}-3{{m}_{He}}.{{c}^{2}}}{3}=\frac{16,5625+12,000.931-3.4,0015.931}{3}$

$\Rightarrow {{K}_{\alpha }}=4,124MeV\approx 6,{{6.10}^{-13}}J$. Chọn C.

Lời giải chi tiết:

Nếu phản ứng thu năng lượng $\Delta E=\sum{{{m}_{\text{truoc}}}}{{c}^{2}}-\sum{{{m}_{sau}}}{{c}^{2}}<0$ thì năng lượng tối thiểu của phôtôn cần thiết để phản ứng thực hiện được là ${{\varepsilon }_{\min }}=-\Delta E$

Ta có: $\Delta E={{m}_{Be}}{{c}^{2}}-2{{m}_{\alpha }}{{c}^{2}}-{{m}_{n}}{{c}^{2}}=-1,6(MeV)\Rightarrow \varepsilon =-\Delta E=1,6(MeV)$. Chọn D.

DẠNG 3: BÀI TOÁN LIÊN QUAN ĐẾN BẢO TOÀN ĐỘNG LƯỢNG VÀ BẢO TOÀN NĂNG LƯỢNG.

PHƯƠNG PHÁP GIẢI

• Bước 1: Viết phương trình định luật bảo toàn vectơ động lượng:

$\overrightarrow{{{P}_{A}}}+\overrightarrow{{{P}_{B}}}=\overrightarrow{{{P}_{X}}}+\overrightarrow{{{P}_{Y}}}\Leftrightarrow {{m}_{A}}\overrightarrow{{{v}_{A}}}+{{m}_{B}}\overrightarrow{{{v}_{B}}}={{m}_{X}}\overrightarrow{{{v}_{X}}}+{{m}_{Y}}\overrightarrow{{{v}_{Y}}}$

Biểu diễn các vec-tơ bằng sơ đồ hình học, từ đó rút ra phương trình độ lớn của các vec-tơ động lượng ta được phương trình (1).

• Bước 2: Viết phương trình định luật bảo toàn năng lượng toàn phần:

${{K}_{t}}+({{m}_{A}}+{{m}_{B}}){{c}^{2}}={{K}_{s}}+({{m}_{X}}+{{m}_{Y}}){{c}^{2}}$

Sử dụng mối liên hệ giữa P và K là $P=\sqrt{2mK}$ hoặc $K=\frac{{{P}^{2}}}{2m}$, ta được phương trình (2).

• Bước 3: Giả hệ phương trình (1) và (2).

BÀI TẬP LUYỆN TẬP DẠNG 3

Lời giải chi tiết:

Bảo toàn số khối và bảo toàn điện tích, ta viết được phương trình phản ứng:

${}_{Z}^{A}x\xrightarrow{{}}{}_{2}^{4}\alpha +{}_{Z-2}^{A-4}Y$

Bảo toàn động lượng (ban đầu X đứng yên $\Rightarrow \overrightarrow{{{P}_{X}}}=0$):

$0=\overrightarrow{{{P}_{\alpha }}}+\overrightarrow{{{P}_{Y}}}\Rightarrow \overrightarrow{{{P}_{\alpha }}}=-\overrightarrow{{{P}_{Y}}}\Rightarrow {{m}_{\alpha }}{{v}_{\alpha }}={{m}_{Y}}{{v}_{Y}}\Rightarrow {{v}_{Y}}=\frac{{{m}_{\alpha }}v}{{{m}_{Y}}}$

Khối lượng của hạt nhân bằng số khối của nó, tức ${{m}_{\alpha }}=4u,{{m}_{Y}}=(A-4)u$, suy ra:${{v}_{Y}}=\frac{4v}{A-4}$. Chọn B.

Lời giải chi tiết

Bảo toàn số khối, điện tích: ${}_{92}^{234}U\xrightarrow{{}}{}_{2}^{4}\alpha +{}_{90}^{230}Th$

Bảo toàn động lượng: $0=\overrightarrow{{{P}_{\alpha }}}+\overrightarrow{{{P}_{Th}}}\Rightarrow \overrightarrow{{{P}_{\alpha }}}=-\overrightarrow{{{P}_{Th}}}$

$\Rightarrow P_{\alpha }^{2}=P_{Th}^{2}\Leftrightarrow 2{{m}_{\alpha }}{{K}_{\alpha }}=2{{m}_{Th}}{{K}_{Th}}\Leftrightarrow 4,0015u.4=229,973u.{{K}_{Th}}\Rightarrow {{K}_{Th}}=0,0696MeV$.

Bảo toàn năng lượng toàn phần: $Ku+mu{{c}^{2}}={{K}_{\alpha }}+{{K}_{Th}}+({{m}_{\alpha }}+{{m}_{Th}}){{c}^{2}}$

$\Leftrightarrow {{m}_{u}}{{c}^{2}}=4+0,0696+(4,0015+229,9737).931,5\Rightarrow {{m}_{u}}=233,97u$. Chọn A.

Lời giải chi tiết:

Bảo toàn số khối, điện tích: ${}_{1}^{1}p+{}_{3}^{7}Li\xrightarrow{{}}2{}_{2}^{4}X$

Bảo toàn động lượng: $\overrightarrow{{{P}_{p}}}+0=\overrightarrow{{{P}_{X}}}+\overrightarrow{{{P}_{X}}}$

Do 2 hạt X hợp tới các prôtôn các góc $60{}^\circ $ $\Rightarrow $ chúng hợp với nhau góc $120{}^\circ $. Ta có:

$P_{p}^{2}=P_{X}^{2}+P_{X}^{2}+2{{P}_{X}}{{P}_{X}}\cos 120{}^\circ $ (2 hạt X sinh ra có cùng tốc độ nên cùng động lượng ${{P}_{X}}$)

$\Leftrightarrow P_{p}^{2}=P_{X}^{2}\Rightarrow {{m}_{p}}{{v}_{p}}={{m}_{X}}{{v}_{X}}\Rightarrow \frac{{{v}_{p}}}{{{v}_{X}}}=\frac{{{m}_{X}}}{{{m}_{p}}}=\frac{4}{1}=4$. Chọn A.

Lời giải chi tiết:

Phương trình phản ứng: $\alpha +{}_{7}^{14}N\xrightarrow{{}}{}_{8}^{17}O+p$

Ta có: ${{K}_{O}}=\frac{{{m}_{O}}v_{O}^{2}}{2};{{K}_{p}}=\frac{{{m}_{p}}v_{p}^{2}}{2}$ mà ${{v}_{O}}={{v}_{p}}\Rightarrow \frac{{{K}_{p}}}{{{K}_{O}}}=\frac{{{m}_{p}}}{{{m}_{O}}}=\frac{1}{17}$ (1)

Bảo toàn năng lượng toàn phần: ${{K}_{\alpha }}+({{m}_{\alpha }}+{{m}_{N}}){{c}^{2}}={{K}_{O}}+{{K}_{p}}+({{m}_{O}}+{{m}_{p}}){{c}^{2}}$

$\Rightarrow {{K}_{O}}+{{K}_{p}}={{K}_{\alpha }}+({{m}_{\alpha }}+{{m}_{N}}-{{m}_{O}}-{{m}_{p}}){{c}^{2}}=18-1,1172$

$\Rightarrow {{K}_{O}}+{{K}_{p}}=16,8828MeV$

Từ (1) và (2), suy ra: ${{K}_{p}}=0,9379MeV$. Chọn D.

Lời giải chi tiết:

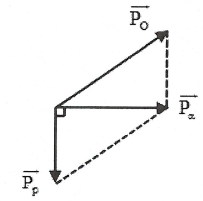
Phương trình phản ứng: $\alpha +{}_{7}^{14}N\xrightarrow{{}}{}_{1}^{1}p+{}_{8}^{17}O$

Bảo toàn động lượng: $\overrightarrow{{{P}_{\alpha }}}=\overrightarrow{{{P}_{p}}}+\overrightarrow{{{P}_{O}}}$

Do hạt p bay ra vuông góc với hạt $\alpha $ nên:

$P_{O}^{2}=P_{\alpha }^{2}+P_{p}^{2}\Leftrightarrow {{m}_{O}}{{K}_{O}}={{m}_{\alpha }}{{K}_{\alpha }}+{{m}_{p}}{{K}_{p}}$ (do P² = 2mK)

$\Leftrightarrow 16,9947u.{{K}_{O}}=4,0015u.7,7+1,0073u.{{K}_{p}}$

$\Leftrightarrow 16,9947{{K}_{O}}-1,0073{{K}_{p}}=30,81155$<