Bài tập Nhận dạng đồ thị hàm số mũ và logarit có đáp án chi tiết

Bài tập Nhận dạng đồ thị hàm số mũ và logarit có đáp án
Câu hỏi bài tập trắc nghiệm về đọc đồ thị hàm số mũ, lũy thừa và logarit có Lời giải chi tiết
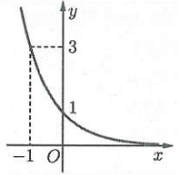
| Bài tập 1: Đồ thị hình bên là của hàm số nào?
A. $y={{\left( \sqrt{3} \right)}^{x}}.$ B. $y={{\left( \frac{1}{2} \right)}^{x}}.$ C. $y={{\log }_{\frac{1}{3}}}x.$ D. $y={{\left( \frac{1}{3} \right)}^{x}}.$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy:
Hàm số có TXĐ: $D=\mathbb{R},$ tập giá trị $T=\left( 0;+\infty \right)$ và hàm số nghịch biến trên $\mathbb{R}$ (loại A và C).
Đồ thị hàm số đi qua điểm $\left( -1;3 \right)$ (loại B). Chọn D.
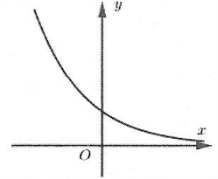
| Bài tập 2: Đồ thị hình bên là của hàm số nào?
A. $y={{\log }_{\frac{1}{2}}}x.$ B. $y={{2}^{-x}}.$ C. $y={{2}^{x}}.$ D. $y={{\log }_{2}}x.$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy:
Hàm số có TXĐ: $D=\left( 0;+\infty \right),$ tập giá trị $T=\mathbb{R}$ và hàm số đồng biến trên $\left( 0;+\infty \right).$ Chọn D.
| Bài tập 3: Đồ thị hình bên là của hàm số nào?
A. $y={{\log }_{0,5}}x.$ B. $y={{2}^{x}}.$ C. $y={{\left( \frac{1}{2} \right)}^{x}}.$ D. $y={{\log }_{2}}x.$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy:
Hàm số có TXĐ: $D=\mathbb{R},$ tập giá trị $T=\left( 0;+\infty \right)$ và hàm số nghịch biến trên $\mathbb{R}.$ Chọn C.
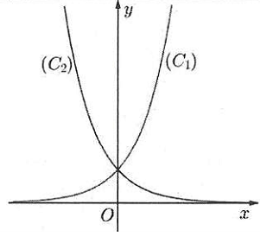
| Bài tập 4: Cho hai hàm số $y={{a}^{x}},$ $y={{b}^{x}}$ với $a,b$ là hai số thực dương khác 1, lần lượt có đồ thị là $\left( {{C}_{1}} \right)$ và $\left( {{C}_{2}} \right)$ như hình bên. Mệnh đề nào dưới đây đúng?
A. $0<a<1<b.$ B. $0<b<1<a.$ C. $0<b<a<1.$ D. $0<a<b<1.$ |
Lời giải chi tiết:
Dựa vào đồ thị suy ra hàm số $y={{a}^{x}}$ là hàm đồng biến, hàm số $y={{b}^{x}}$ là hàm nghịch biến
Suy ra $\left\{ \begin{array} {} a>1 \\ {} 0<b<1 \\ \end{array} \right..$ Chọn B.
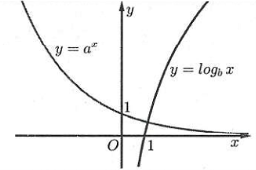
| Bài tập 5: Cho đồ thị hàm số $y={{a}^{x}},$ $y={{\log }_{b}}x$ (như hình vẽ). Khẳng định nào sau đây đúng?
A. $0<b<1<a$ B. $0<a<1<b$ C. $a>1$ và $b>1$ D. $0<a<1$ và $0<b<1$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy $y={{a}^{x}}$ là hàm nghịch biến nên $0<a<1.$
Hàm số $y={{\log }_{b}}x$ là hàm đồng biến nên $b>1.$
Do đó $0<a<1<b.$ Chọn B.
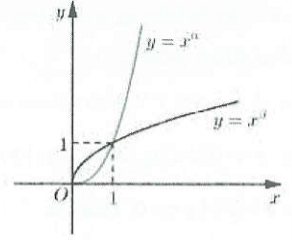
| Bài tập 6: Cho $\alpha ,\beta $ là các số thực. Đồ thị các hàm số $y={{x}^{\alpha }},y={{x}^{\beta }}$ trên khoảng $\left( 0;+\infty \right)$ được cho trong hình vẽ bên. Khẳng định nào đây là đúng?
A. $0<\beta <1<\alpha .$ B. $\beta <0<1<\alpha .$ C. $0<\alpha <1<\beta .$ D. $\alpha <0<1<\beta .$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số, ta thấy
Đồ thị hai hàm số là hàm số đồng biến trên $\left( 0;+\infty \right)$ nên $y'>0;\forall \left( 0;+\infty \right).$
Ta thấy rằng $\left\{ \begin{array} {} y={{x}^{\alpha }}\Rightarrow y'=\alpha .{{x}^{\alpha -1}} \\ {} y={{x}^{\beta }}\Rightarrow y'=\beta .{{x}^{\beta -1}} \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} \alpha .{{x}^{\alpha -1}}>0 \\ {} \beta .{{x}^{\beta -1}} \\ \end{array} \right.\Rightarrow \alpha ,\beta >0.$
Dễ thấy tại $x=2$ thì ${{2}^{\alpha }}>{{2}^{\beta }}\Rightarrow \alpha >\beta $ suy ra $0<\beta <1<\alpha .$ Chọn A.
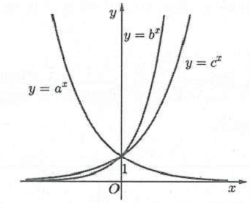
| Bài tập 7: Cho 3 số $a,b,c>0,$ $a\ne 1,b\ne 1,c\ne 1.$ Đồ thị các hàm số $y={{a}^{x}},$ $y={{b}^{x}},$ $y={{c}^{x}}$ được cho trong hình vẽ dưới. Mệnh đề nào sau đây đúng?
A. $b<c<a.$ B. $a<c<b.$ C. $a<b<c.$ D. $c<a<b.$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy hàm số $y={{b}^{x}}$ và $y={{c}^{x}}$ là các hàm số đồng biến nên $b;c>1$
Hàm số $y={{a}^{x}}$ là hàm nghịch biến nên $0<a<1$
Với $x=100$ ta thấy ${{b}^{100}}>{{c}^{100}}\Rightarrow b>c\Rightarrow b>c>1>a>0.$ Chọn B.
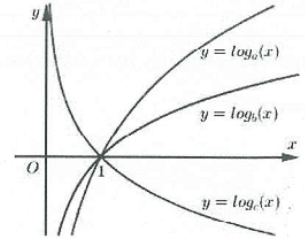
| Bài tập 8: Cho 3 số $a,b,c>0,$ $a\ne 1,b\ne 1,c\ne 1.$ Đồ thị các hàm số $y={{\log }_{a}}x,$$y={{\log }_{b}}x,$$y={{\log }_{c}}x$ được cho trong hình vẽ bên. Mệnh đề nào sau đây đúng?
A. $a>b>c.$ B. $b>a>c.$ C. $c>b>a.$ D. $c>a>b.$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy hàm số $y={{\log }_{a}}x$ và $y={{\log }_{b}}x$ là các hàm số đồng biến trên khoảng $\left( 0;+\infty \right)$ nên $a;b>1$
Hàm số $y={{\log }_{c}}x$ là hàm nghịch biến trên khoảng $\left( 0;+\infty \right)$ nên $0<c<1.$
Thay $x=100\Rightarrow {{\log }_{a}}100>{{\log }_{b}}100>0\Leftrightarrow \frac{1}{{{\log }_{100}}a}>\frac{1}{{{\log }_{100}}b}\Leftrightarrow {{\log }_{100}}b>{{\log }_{100}}a\Leftrightarrow b>a>1$
Vậy $b>a>1>c>0.$ Chọn B.
| Bài tập 9: Cho 2 số $a,b>0,$ $a\ne 1,b\ne 1.$ Đồ thị các hàm số $y={{\log }_{a}}x,$$y={{\log }_{b}}x$ được cho trong hình vẽ bên. Mệnh đề nào sau đây đúng?
A. $1>a>b>0.$ B. $1>b>a>0.$ C. $b>a>1.$ D. $a>b>1.$ |
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy hàm số $y={{\log }_{a}}x$ và $y={{\log }_{b}}x$ là các hàm số nghịch biến trên khoảng $\left( 0;+\infty \right)$ nên $0<a;b<1$
Thay $x=100\Rightarrow 0>{{\log }_{a}}100>{{\log }_{b}}100\Leftrightarrow \frac{1}{{{\log }_{100}}a}>\frac{1}{{{\log }_{100}}b}\Leftrightarrow \frac{{{\log }_{100}}b-{{\log }_{100}}a}{{{\log }_{100}}a.{{\log }_{100}}b}>0$
$\Leftrightarrow {{\log }_{100}}b>{{\log }_{100}}a\Leftrightarrow b>a.$ Chọn B.
| Bài tập 10: Cho hàm số $y={{\log }_{a}}x$ và $y={{\log }_{b}}x$ có đồ thị như hình vẽ bên. Đường thẳng $x=7$ cắt trục hoành, đồ thị hàm số $y={{\log }_{a}}x$ và $y={{\log }_{b}}x$ lần lượt tại $H,M$ và $N.$ Biết rằng $HM=MN.$ Mệnh đề nào sau đây là đúng?
A. $a=7b.$ B. $a={{b}^{2}}.$ C. $a={{b}^{7}}.$ D. $a=2b.$ |
Lời giải chi tiết:
Dựa vào hình vẽ ta thấy $HM=MN\Leftrightarrow NH=2MH\Leftrightarrow {{\log }_{b}}7=2{{\log }_{a}}7\Leftrightarrow \frac{1}{{{\log }_{7}}b}=\frac{2}{{{\log }_{7}}a}$
$\Leftrightarrow a={{b}^{2}}.$ Chọn B.
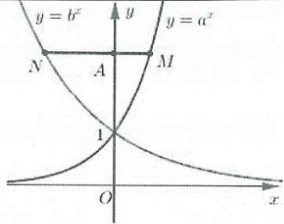
| Bài tập 11: Cho các số thực dương $a,b$ khác 1. Biết rằng bất kì đường thẳng nào song song với $Ox$ mà cắt các đường $y={{a}^{x}},y={{b}^{x}}$ trục tung lần lượt tại $M,N$ và $A$ thì $AN=2AM$ (hình vẽ bên). Mệnh đề nào sau đây đúng?
A. ${{a}^{2}}=b$ B. $a{{b}^{2}}=1$ C. $b=2a$ D. $ab=\frac{1}{2}$ |
Lời giải chi tiết:
Với $y={{y}_{0}}$ ta có: ${{x}_{1}}={{\log }_{b}}{{y}_{0}};{{x}_{2}}={{\log }_{a}}{{y}_{0}}.$
Theo giả thiết ta có $AN=2AM$ nên ${{x}_{1}}=-2{{x}_{2}}\Leftrightarrow {{\log }_{b}}{{y}_{0}}=-2{{\log }_{a}}{{y}_{0}}\Leftrightarrow {{\log }_{b}}{{y}_{0}}={{\log }_{{{a}^{\frac{-1}{2}}}}}{{y}_{0}}$
Khi đó $b={{a}^{-\frac{1}{2}}}=\frac{1}{\sqrt{a}}\Rightarrow a{{b}^{2}}=1.$ Chọn B.
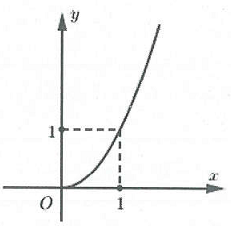
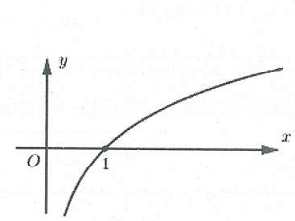
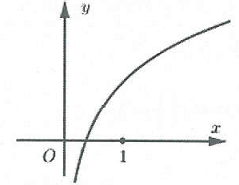
| Bài tập 12: Cho hàm số $f\left( x \right)=x\ln x.$ Một trong bốn đồ thị cho trong bốn phương án A, B, C, D dưới đây là đồ thị của hàm số $y=f'\left( x \right).$ Tìm đồ thị đó.
A. C. |
Lời giải chi tiết:
Với tập xác định cho cả đạo hàm là $D=\left( 0;+\infty \right).$
Loại D vì có phần đồ thị thuộc khoảng $\left( -\infty ;0 \right).$ Loại A vì đồ thị đi qua điểm $\left( 0;0. \right)$
$f\left( x \right)=x\ln x\xrightarrow{{}}{f}'\left( x \right)=1+\ln x.$ Mặt khác: ${f}'\left( 1 \right)=1\ne 0\to $ B không thỏa. Chọn C.
TOÁN LỚP 12




 D.
D. 