Bài tập nhận dạng đồ thị hàm số có chứa dấu trị tuyệt đối

Bài tập nhận dạng đồ thị hàm số chứa dấu trị tuyệt đối có đáp án
Phương pháp giải nhận dạng đồ thị hàm trị tuyệt đối
Mẫu 1: Từ đồ thị hàm số $y=f\left( x \right)\,\,\left( C \right)$ suy ra đồ thị hàm số $y=\left| f\left( x \right)\, \right|\,\left( C \right)$
Ta có: $y=\left| f\left( x \right)\, \right|=\left\{ \begin{align} & f\left( x \right)\,\,\text{khi }f\left( x \right)\ge 0 \\ & -f\left( x \right)\,\,\text{khi }f\left( x \right)<0 \\ \end{align} \right.$. Do đó đồ thị hàm số $y=\left| f\left( x \right)\, \right|\,\left( C \right)$ gồm hai phần:
- Phần 1: Là phần đồ thị hàm số $\left( C \right)$ nằm phía bên trên trục hoành.
- Phần 2: Lấy đối xứng phần của $\left( C \right)$ nằm dưới $Ox$ qua $Ox$
|
Đồ thị hàm số $y=f\left( x \right)\,\,\left( C \right)$ |
Đồ thị hàm số $y=\left| f\left( x \right)\, \right|\,\left( C \right)$ |
|
|
|
Mẫu 2: Từ đồ thị hàm số $y=f\left( x \right)\,\,\left( C \right)$ suy ra đồ thị hàm số $y=f\left( \left| x \right| \right)\,\,\left( {{C}_{1}} \right)$
Ta có: $y=f\left( \left| x \right| \right)\,\,=\left\{ \begin{align} & f\left( x \right)\,\,\text{khi }f\left( x \right)\ge 0 \\ & f\left( -x \right)\,\,\text{khi }f\left( x \right)<0 \\ \end{align} \right.$. Do đó đồ thị hàm số $y=f\left( \left| x \right| \right)\,\,\left( {{C}_{1}} \right)$ gồm hai phần:
- Phần 1: Là phần đồ thị hàm số $\left( C \right)$ nằm bên phải trục tung.
- Phần 2: Lấy đối xứng phần 1 qua trục tung (vì hàm số $y=f\left( \left| x \right| \right)\,$ là hàm chẵn nên nhận trục tung làm trục đối xứng)
|
Đồ thị hàm số $y=f\left( x \right)\,\,\left( C \right)$ |
Đồ thị hàm số $y=f\left( \left| x \right| \right)\,\,\left( {{C}_{1}} \right)$ |
|
|
|
Mẫu 3: Từ đồ thị hàm số $y=u\left( x \right).v\left( x \right)\,\,\left( C \right)$ suy ra đồ thị hàm số $y=\left| u\left( x \right) \right|.v\left( x \right)\,\,\left( {{C}_{1}} \right)$
Ta có: $y=\left| u\left( x \right) \right|.v\left( x \right)\,=\left\{ \begin{align} & u\left( x \right).v\left( x \right)\,\,\text{khi u}\left( x \right)\ge 0 \\ & -u\left( x \right).v\left( x \right)\,\,\text{khi u}\left( x \right)<0 \\ \end{align} \right.$. Do đó đồ thị hàm số $y=\left| u\left( x \right) \right|.v\left( x \right)\,\,\left( {{C}_{1}} \right)$ gồm hai phần:
- Phần 1: Là phần của $\left( C \right)$ ứng với miền $\text{u}\left( x \right)\ge 0$.
- Phần 2: Lấy đối xứng phần của $\left( C \right)$ ứng với miền $\text{u}\left( x \right)<0$ qua trục $Ox$.
Bài tập trắc nghiệm nhận dạng dạng đồ thị hàm số trị tuyệt đối có đáp án
|
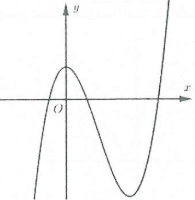
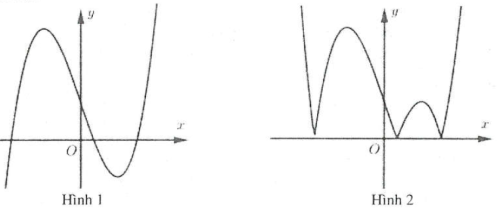
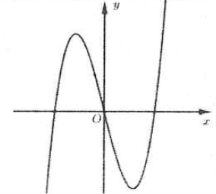
Ví dụ 1: Hình 1 là đồ thị hàm số $y={{x}^{3}}-3x+1$. Đồ thị hình 2 là đồ thị của hàm số nào trong các hàm số sau A. $y={{\left| x \right|}^{3}}-3\left| x \right|+1$. B. $y=\left| {{x}^{3}}-3x+1 \right|$. C. $y=\left| {{\left| x \right|}^{3}}-3\left| x \right|+1 \right|$. D. $y={{\left| x \right|}^{3}}-3x+1$. |
Lời giải
Đồ thị hình 2 gồm 2 phần:
- Phần 1: Là phần đồ thị của hình 1 nằm phía bên trên trục $Ox$.
- Phần 2: Lấy đối xứng phần đồ thị của hình 1 nằm dưới $Ox$ qua $Ox$.
Do đó đồ thị hình 2 là đồ thị hàm số $y=\left| f\left( x \right) \right|=\left| {{x}^{3}}-3x+1 \right|$. Chọn B.
|
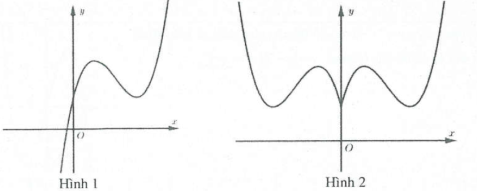
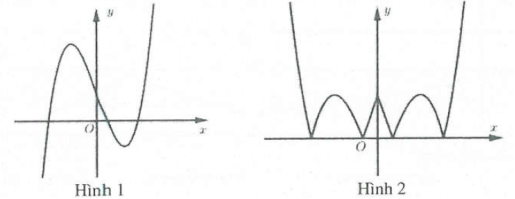
Ví dụ 2: Hình 1 là đồ thị hàm số $y={{x}^{3}}-4{{x}^{2}}+4x+1$. Đồ thị hình 2 là đồ thị của hàm số nào trong các hàm số sau A. $y=\left| {{x}^{3}}-4{{x}^{2}}+4x+1 \right|$. B. $y=\left| {{\left| x \right|}^{3}}-4{{x}^{2}}+4\left| x \right|+1 \right|$. C. $y=\left| x \right|x-4{{x}^{2}}+4\left| x \right|+1$. D. $y={{\left| x \right|}^{3}}+4{{x}^{2}}+4\left| x \right|+1$. |
Lời giải
Đồ thị hình 2 gồm 2 phần:
- Phần 1: Là phần đồ thị của hình 1 nằm bên phải trục $Oy$.
- Phần 2: Lấy đối xứng phần 1 qua $Oy$.
Do đó đồ thị hình 2 là đồ thị hàm số $y=\left| f\left( x \right) \right|=\left| x \right|x-4{{x}^{2}}+4\left| x \right|+1$. Chọn C.
|
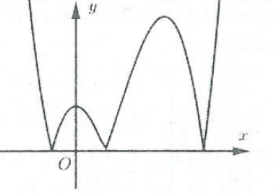
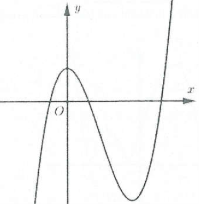
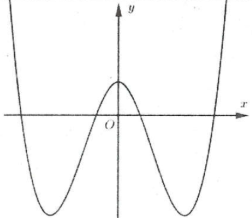
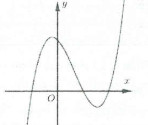
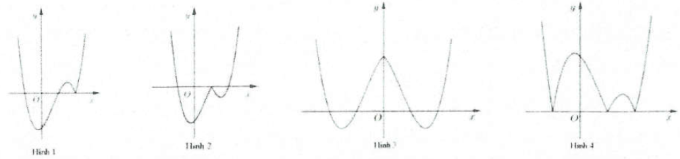
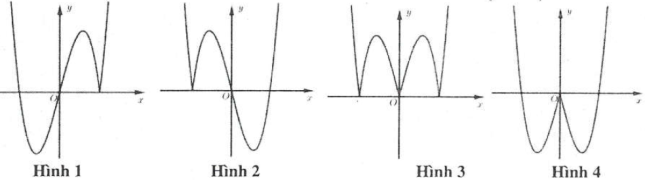
Ví dụ 3: [Đề thi tham khảo của Bộ GD&ĐT năm 2017] Hàm số $y=\left( x-2 \right)\left( {{x}^{2}}-1 \right)$ có đồ thị nào như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số $y=\left| x-2 \right|\left( {{x}^{2}}-1 \right)$? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. |
Lời giải
Đồ thị hàm số $y=\left( x-2 \right)\left( {{x}^{2}}-1 \right)$ cắt trục hoành tại điểm $x=1,x=2$
Áp dụng quy tắc phá giá trị tuyệt đối $y=\left| x-2 \right|\left( {{x}^{2}}-1 \right)=\left\{ \begin{align} & \left( x-2 \right)\left( {{x}^{2}}-1 \right)\text{ khi }x\ge 2 \\ & -\left( x-2 \right)\left( {{x}^{2}}-1 \right)\text{ khi }x<2 \\ \end{align} \right.$
Đồ thị hàm số $y=\left| x-2 \right|\left( {{x}^{2}}-1 \right)$ gồm 2 phần:
- Phần 1: Là phần của đồ thị hàm số $y=\left( x-2 \right)\left( {{x}^{2}}-1 \right)$ với miền $x\ge 2$.
- Phần 2: Lấy đối xứng phần của đồ thị hàm số $y=\left( x-2 \right)\left( {{x}^{2}}-1 \right)$ ứng với miền $x<2$ qua trục hoành. Từ đó suy ra đồ thị hàm số có dạng như hình 1. Chọn A.
|
Ví dụ 4: Hàm số $y={{x}^{3}}-4x$ có đồ thị nào như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số $y=\left| x-2 \right|\left( {{x}^{2}}+2x \right)$? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. |
Lời giải
Ta có: $y=\left| x-2 \right|\left( {{x}^{2}}+2x \right)=\left\{ \begin{align} & {{x}^{3}}-4x\text{ khi }x\ge 2 \\ & -\left( {{x}^{3}}-4x \right)\text{ khi }x<2 \\ \end{align} \right.$
Do đó đồ thị hàm số $y=\left| x-2 \right|\left( {{x}^{2}}+2x \right)$ gồm 2 phần:
- Phần 1: Là phần của đồ thị $\left( C \right):y={{x}^{3}}-4x$ ứng với $x\ge 2$.
- Phần 2: Lấy đối xứng phần của $\left( C \right):y={{x}^{3}}-4x$ ứng với miền $x<2$ qua $Ox$.
Suy ra đồ thị hàm số $y=\left| x-2 \right|\left( {{x}^{2}}+2x \right)$ là hình 1. Chọn A.
|
Ví dụ 5: Hình 1 là đồ thị hàm số $y={{x}^{3}}-3x+1$. Đồ thị hình 2 là đồ thị của hàm số nào trong các hàm số sau A. $y=\left| {{x}^{3}} \right|-3\left| x \right|+1$. B. $y=\left| {{x}^{3}} \right|+3\left| x \right|+1$. C. $y=\left| \left| {{x}^{3}} \right|-3\left| x \right|+1 \right|$. D. $y=\left| \left| {{x}^{3}} \right|+3\left| x \right|+1 \right|$. |
Lời giải
Từ đồ thị hàm số $y={{x}^{3}}-3x+1$ ta suy ra đồ thị hàm số $y=\left| {{x}^{3}} \right|-3\left| x \right|+1$ như hình vẽ sau
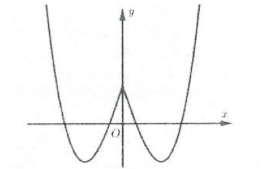
Đồ thị hình 2 gồm 2 phần:
Từ đó suy ra đồ thị hàm số ở hình 2 là đồ thị hàm số $y=\left| \left| {{x}^{3}} \right|-3\left| x \right|+1 \right|$. Chọn C.
TOÁN LỚP 12