Bài tập nhận dạng đồ thị hàm số bậc 4 (trùng phương) có đáp án chi tiết

Bài tập nhận dạng đồ thị hàm số bậc 4 có đáp án
Dưới đây là một số bài tập trắc nghiệm nhận dạng đồ thị hàm số có đáp án chi tiết
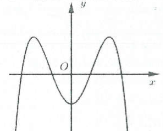
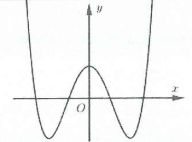
| Bài tập 1: [Đề THPT QG năm 2018] Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A. $y={{x}^{4}}-3{{x}^{2}}-1$. B. $y={{x}^{3}}-3{{x}^{2}}-1$. C. $y=-{{x}^{3}}+3{{x}^{2}}-1$. D. $y=-{{x}^{4}}+3{{x}^{2}}-1$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy:
$\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty \Rightarrow $ Hệ số $a<0$ nên ta loại đáp án A và B.
Mặt khác hàm số có 3 điểm cực trị nên loại đáp án C. Chọn D.
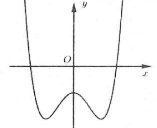
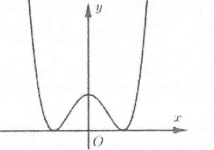
| Bài tập 2: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A. $y={{x}^{4}}-2{{x}^{2}}-1$. B. $y=-{{x}^{4}}+2{{x}^{2}}-1$. C. $y={{x}^{3}}-{{x}^{2}}-1$. D. $y=-{{x}^{3}}+{{x}^{2}}-1$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy:
$\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty \Rightarrow $ Hệ số $a>0$ do đó loại đáp án B và D.
Mặt khác hàm số có 3 điểm cực trị nên loại đáp án C. Chọn A.
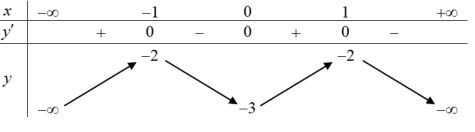
| Bài tập 3: Cho hàm số $y=-{{x}^{4}}+b{{x}^{2}}+c$ có bảng biến thiên như hình vẽ. Tính giá trị của biểu thức $T=b+2c$
A. $T=-4$. B. $T=1$. C. $T=-2$. D. $T=-1$. |
Lời giải chi tiết
Do $y\left( 0 \right)=2\Leftrightarrow c=-3\Rightarrow y=-{{x}^{4}}+b{{x}^{2}}-3$
Mặt khác $f\left( 1 \right)=-2\Leftrightarrow -1+b+c=-2\Rightarrow b+c=-1\Rightarrow b=2$
Suy ra $b+2c=2-6=-4$. Chọn A.
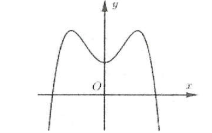
| Bài tập 4: Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$có đồ thị như hình vẽ.
Mệnh đề nào sau đây là đúng? A. $a>0,\,b<0,\,c>0$. B. $a<0,\,b>0,\,c<0$. C. $a<0,\,b>0,\,c>0$. D. $a<0,\,b<0,\,c>0$. |
Lời giải chi tiết
Dựa vào đồ thị ta thấy
$\underset{x\to \infty }{\mathop{\lim }}\,y=-\infty \Rightarrow a<0$; đồ thị hàm số đi qua điểm $\left( 0;d \right)\Rightarrow d>0$.
Hàm số có ba cực trị suy ra $ab<0\xrightarrow{a<0}b>0$
Đồ thị hàm số đi qua điểm có tọa độ $\left( 0;c \right)\Rightarrow c>0$. Chọn C.
| Bài tập 5: Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ.
Khẳng định nào sau đây là đúng? A. $a>0,\,b>0,\,c<0$. B. $a>0,\,b<0,\,c>0$. C. $a<0,\,b>0,\,c>0$. D. $a>0,\,b>0,\,c>0$. |
Lời giải chi tiết
Dựa vào đồ thị ta thấy: $\underset{x\to \infty }{\mathop{\lim }}\,y=+\infty \Rightarrow a>0$; đồ thị hàm số đi qua điểm $\left( 0;d \right)\Rightarrow d>0$.
Hàm số có ba cực trị suy ra $ab<0\xrightarrow{a<0}b>0$
Đồ thị hàm số đi qua điểm có tọa độ $\left( 0;c \right)\Rightarrow c>0$. Chọn D.
| Bài tập 6: Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ.
Khẳng định nào sau đây là đúng? A. $a>0,\,b>0,\,c>0;{{b}^{2}}=4ac$. B. $a>0,\,b<0,\,c>0;{{b}^{2}}=4ac$. C. $a>0,\,b>0,\,c>0;{{b}^{2}}>4ac$. D. $a>0,\,b<0,\,c>0;{{b}^{2}}<4ac$. |
Lời giải chi tiết
Ta có: $\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty $ nên $a>0$; đồ thị hàm số cắt trục $Oy$ tại điểm $\left( 0;c \right)\Rightarrow c>0$.
Hàm số có ba cực trị suy ra $ab<0\Rightarrow b<0$
Giá trị cực trị của hàm số là ${{y}_{CT}}=y\left( \pm \sqrt{\frac{-b}{2a}} \right)=a.\frac{{{b}^{2}}}{4a}-\frac{{{b}^{2}}}{2a}+c=0\Leftrightarrow {{b}^{2}}=4ac$. Chọn B.
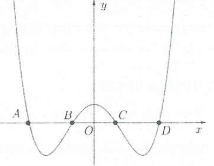
| Bài tập 7: Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ cắt trục hoành tại 4 điểm phân biệt A, B, C, D như hình vẽ bên.
Biết rằng $AB=BC=CD$, mệnh đề nào sau đây đúng? A. $a>0,\,b<0,\,c>0,\,100{{b}^{2}}=9ac$. B. $a>0,\,b>0,\,c>0,\,9{{b}^{2}}=100ac$. C.$a>0,\,b<0,\,c>0,\,9{{b}^{2}}=100ac$. D. $a>0,\,b>0,\,c>0,\,100{{b}^{2}}=9ac$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy
$\underset{x\to +\infty }{\mathop{\lim }}\,y=\underset{x\to +\infty }{\mathop{\lim }}\,\left( a{{x}^{4}}+b{{x}^{2}}+c \right)=+\infty \Rightarrow a>0$
- Đồ thị hàm số cắt trục hoành tại 4 điểm như trong hình khi đó $\left\{ \begin{array} {} -\frac{b}{a}>0 \\ {} \frac{c}{a}>0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} b<0 \\ {} c>0 \\ \end{array} \right.$. Gọi ${{x}_{1}},\,\,{{x}_{2}}$ là nghiệm phương trình $a{{x}^{4}}+b{{x}^{2}}+c=0$ suy ra $\left\{ \begin{array} {} {{x}_{1}}+\,{{x}_{2}}=-\frac{b}{a}\,\,\left( 1 \right) \\ {} {{x}_{1}}.\,{{x}_{2}}=\frac{c}{a}\,\,\left( 2 \right) \\ {} x_{A}^{2}=x_{D}^{2}={{x}_{1}} \\ {} x_{B}^{2}=x_{C}^{2}={{x}_{2}} \\ \end{array} \right.$
Ta có $AB=BC=CD\Rightarrow {{x}_{A}}+{{x}_{C}}=2{{x}_{B}}\Rightarrow \sqrt{{{x}_{1}}}+\sqrt{\,{{x}_{2}}}=-2\sqrt{\,{{x}_{2}}}\Leftrightarrow \sqrt{{{x}_{1}}}=3\sqrt{\,{{x}_{2}}}\Leftrightarrow {{x}_{1}}=9\,{{x}_{2}}$(3)
Từ (1), (2), (3) suy ra $\left\{ \begin{array} {} {{x}_{1}}+\,{{x}_{2}}=-\frac{b}{a}\, \\ {} {{x}_{1}}.\,{{x}_{2}}=\frac{c}{a}\, \\ {} {{x}_{1}}=9\,{{x}_{2}} \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} {{x}_{1}}=-\frac{9b}{10a} \\ {} {{x}_{2}}=-\frac{b}{10a} \\ \end{array} \right.\Rightarrow \frac{c}{a}=\frac{9{{b}^{2}}}{100{{a}^{2}}}\Rightarrow 9{{b}^{2}}=100ac$
Suy ra $a>0,\,b<0,\,c>0,\,9{{b}^{2}}=100ac$. Chọn C.
TOÁN LỚP 12