Bài tập mẫu nguyên tử bohr có đáp án chi tiết

CÁC DẠNG TOÁN CHUYÊN ĐỀ MẪU NGUYÊN TỬ BOHR
DẠNG 1: BÀI TOÁN VỀ TRẠNG THÁI DỪNG. QUỸ ĐẠO DỪNG.
| Bài tập 1: [Trích đề thi THPT QG năm 2008] Trong nguyên tử Hidro, bán kính Bo là ${{r}_{0}}=5,{{3.10}^{-11}}\,m.$ Bán kính quỹ đạo dừng N là
A. $47,{{7.10}^{-11}}\,m.$ B. $21,{{2.10}^{-11}}\,m.$ C. $84,{{8.10}^{-11}}\,m.$ D. $132,{{5.10}^{-11}}\,m.$ |
Lời giải chi tiết:
Bán kính quỹ đạo được xác định theo biểu thức: ${{r}_{n}}={{n}^{2}}{{r}_{0}}$
Qũy đạo N ứng với n=4$\Rightarrow {{r}_{4}}={{4}^{2}}.5,{{3.10}^{-11}}=84,{{8.10}^{-11}}\,m.$ Chọn C.
| Bài tập 2: [Trích đề thi THPT QG năm 2011] Trong nguyên tử Hidro, bán kính Bo là ${{r}_{0}}=5,{{3.10}^{-11}}\,m.$ Ở một trạng thái kích thích của nguyên tử Hidro, electron chuyển động trên quỹ đạo dừng có bán kính là $r=2,{{12.10}^{-10}}\,m.$ Quỹ đạo đó có tên gọi là quỹ đạo dừng
A. L. B. O. C. N. D. M. |
Lời giải chi tiết:
Ta có: ${{r}_{n}}={{n}^{2}}{{r}_{0}}\Rightarrow n=\sqrt{\frac{{{r}_{n}}}{{{r}_{0}}}}=2$: quỹ đạo dừng L. Chọn A.
| Bài tập 3: Vận dụng mẫu nguyên tử Rutherford cho nguyên tử Hidro. Cho hằng số điện $k={{9.10}^{9}}\,N{{m}^{2}}/{{C}^{2}}$ và hằng số điện tích nguyên tố $e=1,{{6.10}^{-19}}\,C$. Khi electron chuyển động trên quỹ đạo tròn bán kính r = 0,53 Å thì năng lượng toàn phần của electron xấp xỉ bằng
A. -12,8 eV. B. -13,6 eV. C. -14,2 eV. D. -15,4 eV. |
Lời giải chi tiết:
Năng lượng toàn phần của electron:
$E=-\frac{k{{e}^{2}}}{2r}=-\frac{{{9.10}^{9}}.{{\left( 1,{{6.10}^{-19}} \right)}^{2}}}{2.0,{{53.10}^{-10}}}=-2,{{17.10}^{-18}}\,J=-\frac{2,{{27.10}^{-18}}}{1,{{6.10}^{-19}}}=-13,6\,eV.$ Chọn B.
| Bài tập 4: Vận dụng mẫu nguyên tử Rutherford cho nguyên tử Hidro. Cho hằng số điện $k={{9.10}^{9}}\,N{{m}^{2}}/{{C}^{2}},$ hằng số điện tích nguyên tố $e=1,{{6.10}^{-19}}\,C$, và khối lượng của electron ${{m}_{e}}=9,{{1.10}^{-31}}\,kg.$ Khi electron chuyển động trên quỹ đạo tròn bán kính r = 2,12 Å thì tốc độ chuyển động của electron xấp xỉ bằng
A. $1,{{1.10}^{6}}\,m/s.$ B. $1,{{4.10}^{6}}\,m/s.$ C. $2,{{2.10}^{5}}\,m/s.$ D. $3,{{3.10}^{6}}\,m/s.$ |
Lời giải chi tiết:
Lực điện đóng vai trò là lực hướng tâm: ${{F}_{d}}={{F}_{ht}}\Leftrightarrow k\frac{{{e}^{2}}}{{{r}^{2}}}=m\frac{{{v}^{2}}}{r}$
$\Rightarrow $ Tốc độ $v=\sqrt{\frac{k{{e}^{2}}}{mr}}=\sqrt{\frac{{{9.10}^{9}}.{{\left( 1,{{6.10}^{-19}} \right)}^{2}}}{9,{{1.10}^{-31}}.2,{{2.10}^{-10}}}}\approx 1,{{1.10}^{6}}\,m/s.$ Chọn A.
| Bài tập 5: [Trích đề thi THPT QG năm 2010] Theo mẫu nguyên tử Bohr, bán kính quỹ đạo K của electron trong nguyên tử Hidro là ${{r}_{0}}.$ Khi electron chuyển từ quỹ đạo N về quỹ đạo L thì bán kính quỹ đạo giảm bớt
A. $12{{r}_{0}}.$ B. $16{{r}_{0}}.$ C. $9{{r}_{0}}.$ D. $4{{r}_{0}}.$ |
Lời giải chi tiết:
Ta có: ${{r}_{n}}={{n}^{2}}{{r}_{0}}\Rightarrow \left. \begin{array}{} {{r}_{N}}={{4}^{2}}{{r}_{0}} \\ {} {{r}_{L}}={{2}^{2}}{{r}_{0}} \\ \end{array} \right\rangle \Rightarrow {{r}_{N}}-{{r}_{L}}=\left( {{4}^{2}}-{{2}^{2}} \right){{r}_{0}}=12{{r}_{0}}.$ Chọn A.
| Bài tập 6: [Trích đề thi THPT QG năm 2012] Theo mẫu nguyên tử Bo, trong nguyên tử Hidro, chuyển động của electron quanh hạt nhân là chuyển động tròn đều. Tỉ số giữa tốc độ của electron trên quỹ đạo K và tốc độ của electron trên quỹ đạo M bằng
A. 9. B. 3. C. 4. D. 2. |
Lời giải chi tiết:
Ta có: ${{v}_{n}}={{v}_{0}}/n\Rightarrow \left. \begin{array}{} {{v}_{K}}=\frac{{{v}_{0}}}{1} \\ {} {{v}_{M}}=\frac{{{v}_{0}}}{3} \\ \end{array} \right\rangle \Rightarrow \frac{{{v}_{K}}}{{{v}_{M}}}=3.$ Chọn B.
| Bài tập 7: [Trích đề thi THPT QG năm 2014] Theo mẫu Bo về nguyên tử Hidro, nếu lực tương tác tĩnh điện giữa electron và hạt nhân khi electron chuyển động trên quỹ đạo dừng L là F thì khi electron chuyển động trên quỹ đạo dừng N, lực này sẽ là
A. F/16. B. F/25. C.F/9. D. F/4. |
Lời giải chi tiết:
Ta có: ${{F}_{n}}={{F}_{0}}/{{n}^{4}}\Rightarrow \left. \begin{array}{} {{F}_{L}}=\frac{{{F}_{0}}}{{{2}^{4}}} \\ {} {{F}_{N}}=\frac{{{F}_{0}}}{{{4}^{4}}} \\ \end{array} \right\rangle \Rightarrow \frac{{{F}_{L}}}{{{F}_{N}}}=\frac{{{4}^{4}}}{{{2}^{4}}}=16\Rightarrow {{F}_{N}}=\frac{{{F}_{L}}}{16}=\frac{F}{16}.$ Chọn A.
DẠNG 2: BÀI TOÁN VỀ SỰ HẤP THỤ VÀ BỨC XẠ.
| Bài tập 8: Cho một chùm ánh sáng trắng đi qua một bình khí Hidro nung nóng ở nhiệt độ thấp hơn nhiệt độ của nguồn phát ánh sáng trắng rồi chiếu qua một máy quang phổ. Trên màn ảnh của máy quang phổ, trong vùng nhìn thấy sẽ có |
| A. 4 vạch màu. B. 4 vạch đen. C. 12 vạch đen. D. 7 vạch màu. |
Lời giải chi tiết:
Quang phổ thu được là quang phổ vạch hấp thụ của Hidro, trên nền quang phổ liên tục sẽ có 4 vạch đen tương ứng với vị trí 4 vạch màu khi nguyên tử Hiđro phát xạ. Chọn B.
| Bài tập 9: [Trích đề thi THPT QG năm 2010] Khi electron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử Hidro được tính theo công thức ${{E}_{n}}=-13,6/{{n}^{2}}\left( eV \right)\,\,\left( n=1,2,3,... \right)$. Khi electron trong nguyên tử Hidro chuyển từ quỹ đạo dừng n = 3 sang quỹ đạo dừng n = 2 thì nguyên tử Hidro phát ra phôtôn ứng với bức xạ có bước sóng bằng
A. $0,4350\,\,\mu m.$ B. $0,6576\,\,\mu m.$ C. $0,4102\,\,\mu m.$ D. $0,4861\,\,\mu m.$ |
Lời giải chi tiết:
Phôtôn bức xạ ra khi electron chuyển từ mức n = 3 sang mức n = 2, có năng lượng thỏa mãn:
$\varepsilon ={{E}_{3}}-{{E}_{2}}\Leftrightarrow \frac{hc}{{{\lambda }_{32}}}=13,6\left( \frac{1}{4}-\frac{1}{9} \right).1,{{6.10}^{-19}}={{3.0222.10}^{-19}}$
$\Rightarrow {{\lambda }_{32}}=\frac{hc}{{{3.0222.10}^{-19}}}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{{{3.0222.10}^{-19}}}=0,{{6576.10}^{-6}}\,m=0,6576\,\mu m.$ Chọn B.
| Bài tập 10: [Trích đề thi THPT QG năm 2012] Theo mẫu nguyên tử Bo, trong nguyên tử Hidro, khi electron chuyển từ quỹ đạo P về quỹ đạo K thì nguyên tử phát ra phôtôn ứng với bức xạ có tần số f1. Khi electron chuyển từ quỹ đạo P về quỹ đạo L thì nguyên tử phát ra phôtôn ứng với bức xạ có tần số f2. Nếu electron chuyển từ quỹ đạo L về quỹ đạo K thì nguyên tử phát ra phôtôn ứng với bức xạ có tần số
A. ${{f}_{3}}={{f}_{1}}-{{f}_{2}}.$ B. ${{f}_{3}}=\sqrt{f_{1}^{2}+f_{2}^{2}}.$ C. ${{f}_{3}}={{f}_{1}}+{{f}_{2}}.$ D. ${{f}_{3}}=\frac{{{f}_{1}}.{{f}_{2}}}{{{f}_{1}}+{{f}_{2}}}.$ |
Lời giải chi tiết:
${{\varepsilon }_{1}}=h{{f}_{1}}={{E}_{P}}-{{E}_{K}}\,;\,\,{{\varepsilon }_{2}}=h{{f}_{2}}={{E}_{P}}-{{E}_{K}}$
${{\varepsilon }_{3}}={{E}_{L}}-{{E}_{K}}=\left( {{E}_{P}}-{{E}_{K}} \right)-\left( {{E}_{P}}-{{E}_{K}} \right)$
$\Leftrightarrow {{\varepsilon }_{3}}={{\varepsilon }_{1}}-{{\varepsilon }_{2}}\Leftrightarrow h{{f}_{3}}=h{{f}_{1}}-h{{f}_{2}}\Leftrightarrow {{f}_{3}}={{f}_{1}}-{{f}_{2}}.$ Chọn A.
| Bài tập 11: Cho năng lượng các trạng thái dừng của nguyên tử Hidro có biểu thức ${{E}_{n}}=-13,6/{{n}^{2}}eV.$ Cho các hằng số $h=6,{{625.10}^{-34}}\,Js,\,\,c={{3.10}^{8}}\,m/s$ và $e=1,{{6.10}^{-19}}\,C.$ Một khối khí Hidro loãng đang bức xạ ra một số loại phôtôn trong đó phôtôn có bước sóng ngắn nhất là ${{\lambda }_{\min }}=0,103\,\,\mu m.$ Số phôtôn khác loại mà khối khí bức xạ là
A. 3 loại. B. 6 loại. C. 10 loại. D. 5 loại. |
Lời giải chi tiết:
Bước sóng ngắn nhất ứng với khe năng lượng lớn nhất:
$\frac{hc}{{{\lambda }_{\min }}}={{\varepsilon }_{\text{max}}}={{E}_{n}}-{{E}_{1}}={{E}_{0}}\left( 1-\frac{1}{{{n}^{2}}} \right)\Leftrightarrow \frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{103.10}^{-6}}}=13,6.1,{{6.10}^{-19}}\left( 1-\frac{1}{{{n}^{2}}} \right)\Rightarrow n=3$
Số phôtôn khác loại mà khối khí bức xạ là: $\frac{n\left( n-1 \right)}{2}=\frac{3\left( 3-1 \right)}{2}=3$loại. Chọn A.
| Bài tập 12: Cho năng lượng các trạng thái dừng của nguyên tử Hidro có biểu thức ${{E}_{n}}=-13,6/{{n}^{2}}eV.$ Cho các hằng số $h=6,{{625.10}^{-34}}\,Js,\,\,c={{3.10}^{8}}\,m/s$ và $e=1,{{6.10}^{-19}}\,C.$ Một khối khí Hidro loãng đang bức xạ ra một số loại phôtôn trong đó phôtôn có bước sóng dài nhất là ${{\lambda }_{\max }}=1,876\,\,\mu m.$ Hỏi có bao nhiêu loại phôtôn phát ra ?
A. 1 loại. B. 5 loại. C. 6 loại. D. 3 loại. |
Lời giải chi tiết:
Bước sóng dài nhất ứng với khe năng lượng nhỏ nhất:
$\frac{hc}{{{\lambda }_{\max }}}={{\varepsilon }_{\text{min}}}={{E}_{n}}-{{E}_{n-1}}={{E}_{0}}\left( \frac{1}{{{\left( n-1 \right)}^{2}}}-\frac{1}{{{n}^{2}}} \right)\Leftrightarrow \frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{1,{{876.10}^{-6}}}=13,6.1,{{6.10}^{-19}}\left( \frac{1}{{{\left( n-1 \right)}^{2}}}-\frac{1}{{{n}^{2}}} \right)\Rightarrow n=4$
Sô phôtôn khác loại mà khối khí bức xạ là: $\frac{n\left( n-1 \right)}{2}=\frac{4\left( 4-1 \right)}{2}=6$ loại. Chọn C.
| Bài tập 13: Biết bước sóng ngắn nhất (vạch cuối cùng) trong dãy Lyman là ${{\lambda }_{L\min }}=91\,\,nm.$ Bước sóng của vạch thứ 3 (vạch thứ nhất là vạch có bước sóng dài nhất) trong dãy Lyman là |
| A. $0,201\,\,\mu m.$ B. $0,097\,\,\mu m.$ C. $0,102\,\,\mu m.$ D. $0,121\,\,\mu m.$ |
Lời giải chi tiết:
Bước sóng dài nhất trong dãy Lyman là ${{\lambda }_{L\min }}={{\lambda }_{21}}$
$\Rightarrow $ Bước sóng của vạch thứ 3 trong dãy Lyman là ${{\lambda }_{41}}$
Ta có: $\frac{1}{{{\lambda }_{41}}}=\frac{1}{{{\lambda }_{L\min }}}\left( 1-\frac{1}{{{4}^{2}}} \right)=\frac{1}{91}.\frac{15}{16}\Rightarrow {{\lambda }_{41}}=\frac{16}{15}.91=97\,\,nm=0,097\,\,\mu m.$ Chọn B.
| Bài tập 14: Vận dụng mẫu nguyên tử Bohr để giải thích quang phổ vạch phát xạ của dãy Hidro. Cho biết vạch đầu tiên (${{H}_{\alpha }}$ - bước sóng dài nhất) trong dãy Balmer có bước sóng là $0,6563\,\,\mu m.$ Bước sóng của vạch thứ 4 (${{H}_{\delta }}$) trong dãy Balmer là
A. $0,563\,\,\mu m.$ B. $0,487\,\,\mu m.$ C. $0,435\,\,\mu m.$ D. $0,410\,\,\mu m.$ |
Lời giải chi tiết:
Vạch dài nhất trong dãy Banme là ${{\lambda }_{32}}$:
$\frac{1}{{{\lambda }_{32}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{3}^{2}}} \right)\Rightarrow {{\lambda }_{32}}=\frac{36}{5}{{\lambda }_{L\min }}\Rightarrow {{\lambda }_{L\min }}=\frac{5}{36}{{\lambda }_{32}}$
$\Rightarrow $ Vạch thứ 4 có bước sóng là ${{\lambda }_{62}}$:
$\frac{1}{{{\lambda }_{62}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{6}^{2}}} \right)\Rightarrow {{\lambda }_{62}}=\frac{9}{2}{{\lambda }_{L\min }}=\frac{9}{2}\left( \frac{5}{36}{{\lambda }_{32}} \right)=\frac{9}{2}\left( \frac{5}{36}.0,6563 \right)=0,410\,\,\mu m.$Chọn D.
| Bài tập 15: Ba vạch đầu tiên trong dãy Balmer là ${{H}_{\alpha }}\left( {{\lambda }_{32}}=0,6563\,\,\mu m \right)$, ${{H}_{\beta }}\left( {{\lambda }_{42}}=0,4861\,\,\mu m \right)$, ${{H}_{\gamma }}\left( {{\lambda |
| }_{52}}=0,4340\,\,\mu m \right)$. Bước sóng của hai vạch đầu tiên (dài nhất) trong dãy Paschen là
A. $1,2813\,\,\mu m$và $1,8744\,\,\mu m.$ B. $0,8726\,\,\mu m$và $1,8744\,\,\mu m.$ C. $1,2813\,\,\mu m$và $1,4623\,\,\mu m.$ D. $0,8726\,\,\mu m$và $1,2813\,\,\mu m.$ |
Lời giải chi tiết:
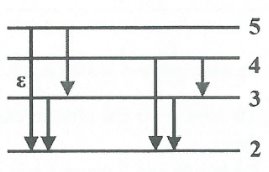
Bước sóng của 2 vạch đầu tiên (dài nhất, ứng với khe năng lượng nhỏ nhất) trong dãy Pasen là ${{\lambda }_{43}}$ và ${{\lambda }_{53}}$.
+) ${{\varepsilon }_{53}}={{\varepsilon }_{52}}-{{\varepsilon }_{32}}$
$\Rightarrow \frac{1}{{{\lambda }_{53}}}=\frac{1}{{{\lambda }_{52}}}-\frac{1}{{{\lambda }_{32}}}=\frac{1}{0,4340}-\frac{1}{0,6563}\Rightarrow {{\lambda }_{53}}=1,2813\,\,\mu m.$
+) ${{\varepsilon }_{43}}={{\varepsilon }_{42}}-{{\varepsilon }_{32}}$
$\Rightarrow \frac{1}{{{\lambda }_{43}}}=\frac{1}{{{\lambda }_{42}}}-\frac{1}{{{\lambda }_{32}}}=\frac{1}{0,4861}-\frac{1}{0,6563}\Rightarrow {{\lambda }_{43}}=1,8744\,\,\mu m.$
Chọn A.
| Bài tập 16: Vạch đầu tiên (bước sóng dài nhất) trong dãy Lyman là ${{\lambda }_{21}}=121,2\,\,nm$. Hai vạch đầu trong dãy Balmer là ${{\lambda }_{32}}=0,6563\,\,\mu m$và ${{\lambda }_{42}}=0,4861\,\,\mu m$. Bước sóng của vạch thứ hai và vạch thứ ba trong dãy Lyman là
A. $341\,\,nm;\,\,910\,\,nm.$ B. $102,3\,\,nm;\,\,97,0\,\,nm.$ C. $0,672\,\,\mu m;\,\,0,455\,\,\mu m.$ D. $0,486\,\,\mu m;\,\,0,970\,\,nm.$ |
Lời giải chi tiết:
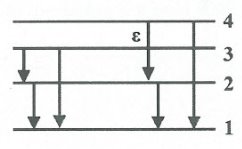
Vạch thứ hai trong dãy Lyman là ${{\lambda }_{31}}$:
${{\varepsilon }_{31}}={{\varepsilon }_{32}}+{{\varepsilon }_{21}}\Rightarrow \frac{1}{{{\lambda }_{31}}}=\frac{1}{0,6563}+\frac{1}{0,1212}$
$\Rightarrow {{\lambda }_{31}}=0,1023\,\,\mu m=102,3\,\,nm.$
Vạch thứ ba trong dãy Lyman là ${{\lambda }_{41}}$:
${{\varepsilon }_{41}}={{\varepsilon }_{42}}+{{\varepsilon }_{21}}\Rightarrow \frac{1}{{{\lambda }_{41}}}=\frac{1}{0,4861}+\frac{1}{0,1212}$
$\Rightarrow {{\lambda }_{41}}=0,0970\,\,\mu m=97,0\,\,nm.$ Chọn B.
| Bài tập 17: Chiếu một chùm sáng đơn sắc vào khối khí Hidro loãng đang ở trạng thái cơ bản thì trong quang phổ phát xạ của khối khí đó có 6 vạch nằm trong vùng hồng ngoại, bước sóng ngắn nhất trong 6 vạch đó bằng $1,0960\,\,\mu m$. Theo mẫu nguyên tử Bohr thì bước sóng ngắn nhất trong quang phổ phát xạ của khối khí Hidro đó là
A. $0,9701\,\,\mu m.$ B. $0,1218\,\,\mu m.$ C. $0,0939\,\,\mu m.$ D. $0,0913\,\,\mu m.$ |
Lời giải chi tiết:
6 vạch vùng hồng ngoại thì mức đáy của nó phải từ mức 3 trở lên.
Ta có: $\frac{n\left( n-1 \right)}{2}=6\Rightarrow n=4$ mức (từ 3 về 6) $\Rightarrow $ Khối khí bị kích thích lên mức 6.
Bước sóng ngắn nhất trong 6 vạch hồng ngoại này là ${{\lambda }_{63}}$: $\frac{hc}{{{\lambda }_{63}}}={{E}_{6}}-{{E}_{3}}={{E}_{0}}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{6}^{2}}} \right)=\frac{{{E}_{0}}}{12}$ (1)
Bước sóng ngắn nhất trong quang phổ của Hidro là ${{\lambda }_{61}}$ : $\frac{hc}{{{\lambda }_{61}}}={{E}_{6}}-{{E}_{1}}={{E}_{0}}\left( \frac{1}{{{1}^{2}}}-\frac{1}{{{6}^{2}}} \right)=\frac{35{{E}_{0}}}{36}$(2)
Chia vế với vế của (1) cho (2): $\frac{{{\lambda }_{61}}}{{{\lambda }_{63}}}=\frac{36}{35}.\frac{1}{12}=\frac{3}{35}\Rightarrow {{\lambda }_{61}}=\frac{3}{35}{{\lambda }_{63}}=\frac{3}{35}.1,0960=0,0939\,\,\mu m.$
Chọn C.
| Bài tập 18: Theo mẫu nguyên tử Bohr, nếu một khối khí Hidro loãng đang bức xạ ra ba loại phôtôn ánh sáng khác nhau với hai trong ba loại phôtôn đó có bước sóng là 0,1217 μm và 0.1027 μm thì phôtôn còn lại có bước sóng là
A. 1,2844 μm. B. 0,6578 μm. C. 0,4861 μm. D. 0,4341 μm. |
Lời giải chi tiết:
Ta có: $\frac{n(n-1)}{2}=3\Rightarrow n=3$, khối khí bị kích thích lên mức 3.
Từ mức 3 có thể phát ra các phôtôn có bước sóng: ${{\lambda }_{21}},{{\lambda }_{31}}$(vùng tử ngoại) và ${{\lambda }_{32}}$ (vùng as nhìn thấy).
Đề bài đã cho 2 trong 3 bức xạ có bước sóng là 0,1217 μm và 0,1027 μm $\in $ vùng tử ngoại nên bước sóng còn lại là ${{\lambda }_{32}}$.
Ta có: ${{\varepsilon }_{32}}={{\varepsilon }_{31}}-{{\varepsilon }_{21}}\Leftrightarrow \frac{1}{{{\lambda }_{32}}}=\frac{1}{{{\lambda }_{31}}}-\frac{1}{{{\lambda }_{21}}}=\frac{1}{0,1217}-\frac{1}{0,1027}\Rightarrow {{\lambda }_{32}}=0,6578\,\,\mu m$. Chọn B.
| Bài tập 19: Cho tỉ số giữa bước sóng dài nhất và bước sóng ngắn nhất trong quang phổ do một khối khí Hidro loãng phát ra là 135/7. Theo mẫu nguyên tử Bohr, số vạch tối đa mà khối khí Hidro trên có thể phát ra là
A. 3 vạch. B. 6 vạch. C. 10 vạch. D. 14 vạch. |
Lời giải chi tiết:
Bước sóng tỉ lệ nghịch với năng lượng nên: ${{\lambda }_{\max }}={{\lambda }_{n1}},\,\,{{\lambda }_{\min }}={{\lambda }_{n(n-1)}}$
$\frac{hc}{{{\lambda }_{n(n-1)}}}={{E}_{0}}\left( \frac{1}{{{(n-1)}^{2}}}-\frac{1}{{{n}^{2}}} \right)\,\,\,(1)$ $\frac{hc}{{{\lambda }_{n1}}}={{E}_{0}}\left( 1-\frac{1}{{{n}^{2}}} \right)\,\,\,(2)$
Chia vế với vế của (1) cho (2) ta được: $\frac{{{\lambda }_{n1}}}{{{\lambda }_{n(n-1)}}}=\frac{\left( \frac{1}{{{(n-1)}^{2}}}-\frac{1}{{{n}^{2}}} \right)}{\left( 1-\frac{1}{{{n}^{2}}} \right)}=\frac{135}{7}\,\,\,(*)$
Thử n = 4 vào (*) thấy thỏa mãn.
Số vạch tối đa khối khí phát ra $=\frac{n(n-1)}{2}=\frac{4(4-1)}{2}=6$. Chọn B.
DẠNG 3: KÍCH THÍCH NGUYÊN TỬ HIDRO.
a) Kích thích nguyên tử Hidro bằng cách cho hấp thụ phôtôn.
Giả sử nguyên tử Hidro đang ở trạng thái cơ bản ${{E}_{1}}$, nếu hấp thụ được phôtôn có năng lượng $\varepsilon $thì nó sẽ chuyển lên trạng thái dừng ${{E}_{n}}$sao cho: ${{E}_{n}}={{E}_{1}}+\varepsilon $.
Nếu ${{E}_{n}}=-13,6/{{n}^{2}}$thì:
$\frac{-13,6}{{{n}^{2}}}=-13,6+\varepsilon \Rightarrow n=\sqrt{\frac{-13,6}{-13,6+\varepsilon }}\left\{ \begin{array}{} n\in \mathbb{N}*\Rightarrow C\tilde{a}\,h\hat{E}p\,th\hat{o}\,ph\ll t\ll n\text{ }\varepsilon \text{ } \\ {} n\notin \mathbb{N}*\Rightarrow Kh\ll ng\,h\hat{E}p\,th\hat{o}\,ph\ll t\ll n\text{ }\varepsilon \\ \end{array} \right.$
| Bài tập 20: Các nguyên tử Hidro đang ở trạng thái cơ bản, năng lượng ion hoá của nó là${{E}_{0}}=13,6\,\,eV$. Chiếu tới các nguyên tử đó một chùm sáng gồm ba loại phôtôn có năng lượng lần lượt là ${{\varepsilon }_{1}}=11,00\,\,eV;$ ${{\varepsilon }_{2}}=12,09\,\,eV;$ ${{\varepsilon }_{3}}=12,20\,\,eV$. Hỏi phôtôn nào sẽ bị hấp thụ ?
A. ${{\varepsilon }_{1}}=11,00\,\,eV.$ B. ${{\varepsilon }_{2}}=12,09\,\,eV.$ C. ${{\varepsilon }_{3}}=12,20\,\,eV.$. D. Không hấp thụ phôtôn nào. |
Lời giải chi tiết:
Những phôtôn bị hấp thụ phải có năng lượng $\varepsilon ={{E}_{n}}-{{E}_{1}}\,\,(n\in \mathbb{Z})$
$\Leftrightarrow {{E}_{0}}\left( 1-\frac{1}{{{n}^{2}}} \right)=\varepsilon \Leftrightarrow \frac{1}{{{n}^{2}}}=1-\frac{\varepsilon }{{{E}_{0}}}=\frac{{{E}_{0}}-\varepsilon }{{{E}_{0}}}\Rightarrow n=\sqrt{\frac{{{E}_{0}}}{{{E}_{0}}-\varepsilon }}=\sqrt{\frac{13,6}{13,6-\varepsilon }}$
Với ${{\varepsilon }_{2}}=12,09\,\,eV\Rightarrow n=3$thỏa mãn $n\in \mathbb{N}*$. Chọn B.
| Bài tập 21: Electron trong nguyên tử Hidro có năng lượng được xác định bằng ${{E}_{n}}=-13,6/{{n}^{2}}\,eV$ $(n=$ $1,2,3,...)$. Từ trạng thái cơ bản, nguyên tử Hidro hấp thụ phôtôn có năng lượng 13,056 eV. Sau đó, trong quá trình trở về trạng thái cơ bản nguyên tử này có thể phát ra mấy bức xạ trong vùng hồng ngoại; bước sóng ngắn nhất thuộc vùng hồng ngoại là</ |
Lời giải:
Trạng thái cơ bản $n=1\Rightarrow {{E}_{1}}=-13,6\,\,eV$
Ta có: ${{E}_{n}}={{E}_{1}}+\varepsilon \Leftrightarrow \frac{-13,6}{{{n}^{2}}}=-13,6+13,056=-0,544\Rightarrow n=5$
Số bức xạ trong vùng hồng ngoại (n về 3): ${{\lambda }_{53}};{{\lambda }_{54}};$${{\lambda }_{43}}$
Bước sóng ngắn nhất ứng với ${{\lambda }_{53}}$:$\frac{hc}{{{\lambda }_{53}}}={{E}_{5}}-{{E}_{3}}={{E}_{0}}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{5}^{2}}} \right)=\frac{16}{225}{{E}_{0}}$
$\Rightarrow {{\lambda }_{53}}=\frac{225hc}{16{{E}_{0}}}=\frac{225.6,{{625.10}^{-34}}{{.3.10}^{8}}}{16.13,6.1,{{6.10}^{-19}}}=1,{{284.10}^{-6}}\,m=1284\,\,nm.$Chọn C.
|
Bài tập 22: [Trích đề thi THPT QG năm 2013] Các mức năng lượng của trạng thái dừng của nguyên tử Hidro được xác định bằng biểu thức ${{E}_{n}}=-13,6/{{n}^{2}}\,eV\,\,(n=1,2,3,...)$. Cho các hằng số $h=6,{{625.10}^{-34}}\,Js,$ $c={{3.10}^{8}}\,m/s$ và $e=1,{{6.10}^{-19}}\,C$. Nếu nguyên tử Hidro hấp thụ một phôtôn có năng lượng 2,55 eV thì bước sóng nhỏ nhất của bức xạ nguyên tử Hidro có thể phát ra là A. $9,{{74.10}^{-8}}\,\,m.$ B. $1,{{46.10}^{-8}}\,\,m.$ C. $1,{{22.10}^{-8}}\,\,m.$ D. $4,{{87.10}^{-8}}\,\,m.$ |
Lời giải:
Ta có: ${{E}_{1}}=-13,6\,\,eV;{{E}_{2}}=-3,4\,\,eV;{{E}_{3}}=-1,51\,\,eV;{{E}_{4}}=-0,85\,\,eV;{{E}_{5}}=-5,44\,\,eV$
Ta thấy ${{E}_{4}}-{{E}_{2}}=-0,85\,\,eV+3,4\,\,eV=2,55\,\,eV$
$\Rightarrow $ Khi hấp thụ phôtôn có năng lượng 2,55 eV thì nguyên tử chuyển từ trạng thái L lên trạng thái N. Từ trạng thái N, nguyên tử muốn bức xạ ra phôtôn có bước sóng nhỏ nhất thì nguyên tử phải xuống trạng thái nào đó sao cho hiệu giữa hai mức năng lượng đạt giá trị lớn nhất. Điều này đạt được khi nguyên tử chuyển từ trạng thái N về K.
Khi đó ta có: ${{\lambda }_{\min }}=\frac{hc}{{{E}_{4}}-{{E}_{1}}}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{(-0,85+13,6).1,{{6.10}^{-19}}}=9,{{74.10}^{-8}}\,\,m$. Chọn A.
b) Kích thích nguyên tử Hidro bằng cách va chạm.
- Nếu nguyên tử Hidro ở trạng thái cơ bản va chạm với một electron có động năng ${{\text{W}}_{0}}$, trong quá trình tương tác giả sử nguyên tử đứng yên và chuyển lên trạng thái dừng ${{E}_{n}}$thì động năng còn lại của electron sau va chạm là $\text{W}={{\text{W}}_{0}}-({{E}_{n}}-{{E}_{1}}).$
- Nếu dùng chùm electron mà mỗi electron có động năng ${{\text{W}}_{0}}$ để bắn phá khối Hidro đang ở trạng
thái cơ bản muốn nó chỉ chuyển lên ${{E}_{n}}$mà không lên được ${{E}_{n}}+1$ thì ${{E}_{n}}-{{E}_{1}}\le {{\text{W}}_{0}}\le {{E}_{n+1}}-{{E}_{1}}$.
Sau đó khối khí Hidro sẽ phát ra tối đa $\frac{n(n-1)}{2}$vạch quang phổ.
|
Bài tập 23: Một electron có động năng 12,4 eV đến va chạm với nguyên tử Hidro đứng yên, ở trạng tháng cơ bản. Trong quá trình tương tác giả sử nguyên tử đứng yên và chuyển lên trạng thái kích thích thứ hai. Biết các mức năng lượng của nguyên tử Hidro ở trạng thái dừng được xác định bằng công thức: ${{E}_{n}}=-13,6/{{n}^{2}}(eV)$với n là số nguyên. Động năng còn lại của electron sau va chạm là A. 2,20 eV. B. 0,31 eV. C. 0,48 eV. D. 1,11 eV. |
Lời giải:
Trạng thái kích thích thứ hai có mức năng lượng là E3.
Động năng còn lại của electron sau va chạm là:
$\text{W}={{\text{W}}_{0}}-({{E}_{3}}-{{E}_{1}})=12,4-\left( \frac{-13,6}{{{3}^{2}}}-\frac{-13,6}{{{1}^{2}}} \right)=0,31\,\,eV$. Chọn B.
|
Bài tập 24: Dùng chùm electron (mỗi electron có động năng W) bắn phá khối khí Hidro ở trạng thái cơ bản thì electron trong các nguyên tử chỉ có thể chuyển ra quỹ đạo xa nhất là quỹ đạo N. Biết các mức năng lượng của nguyên tử Hidro ở trạng thái dừng được xác định bằng công thức: ${{E}_{n}}=-13,6/{{n}^{2}}(eV)$ với n là số nguyên. Giá trị W có thể là A. 12,74 eV. B. 12,2 eV. C. 13,056 eV. D. 12,85 eV. |
Lời giải:
Ta có: ${{E}_{4}}-{{E}_{1}}\le \text{W}\le {{E}_{5}}-{{E}_{1}}\Leftrightarrow 12,75\,\,eV\le \text{W13,056}\,\,\text{eV}$. Chọn D.
VẬT LÝ LỚP 12
