Bài tập liên quan Hình trụ nội tiếp hình cầu có đáp án chi tiết

Bài tập liên quan Hình trụ nội tiếp hình cầu có đáp án chi tiết
Bài tập trắc nghiệm về hình trị nội tiếp hình cầu hay ra trong đề thi có đáp án chi tiết
| Bài tập 1: Cho hình trụ có chiều cao bằng 4 nội tiếp trong hình cầu bán kính bằng 3. Tính thể tích V của khối trụ này
A. 4π. B. 8π. C. 12π. D. 20π. |
Lời giải chi tiết
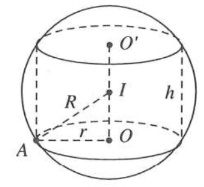
Gọi r, h, R lần lượt là bán kính đáy hình trụ, chiều cao hình trụ và bán kính của hình cầu. Theo hình vẽ, ta được $I{{A}^{2}}=I{{\text{O}}^{2}}+O{{A}^{2}}$
$\xrightarrow{{}}$ (công thức tổng quát bài toán trụ nội tiếp cầu)
Với $h=4,R=3\xrightarrow{{}}{{3}^{2}}={{r}^{2}}+\frac{{{4}^{2}}}{4}\Rightarrow r=\sqrt{5}$
Vậy thể tích khối trụ là $V=\pi {{r}^{2}}h=20\pi .$Chọn D.
| Bài tập 2: Hình trụ (T) có bán kính đáy bằng 3a, chiều cao bằng 8a có hai đáy nằm trên mặt cầu (S). Thể tích của khối cầu bằng
A. $125\pi {{a}^{3}}$ B. $25\pi {{a}^{3}}.$ C. $\frac{500\pi {{a}^{3}}}{3}.$ D. $\frac{375\pi {{a}^{3}}}{4}.$ |
Lời giải chi tiết
Áp dụng công thức tổng quát bài toán trụ nội tiếp cầu, ta được
${{R}^{2}}={{r}^{2}}+\frac{{{h}^{2}}}{4}={{\left( 3\text{a} \right)}^{2}}+\frac{{{\left( \text{8a} \right)}^{2}}}{4}=9{{\text{a}}^{2}}+16{{\text{a}}^{2}}=25{{\text{a}}^{2}}\xrightarrow{{}}R=5\text{a}$
Vậy thể tích khối cầu là $V=\frac{4}{3}\pi {{R}^{3}}=\frac{500\pi {{a}^{3}}}{3}.$ Chọn C.
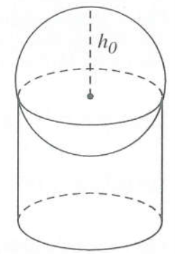
| Bài tập 3: Một quả cầu có thể tích $\frac{256\pi }{3}c{{m}^{3}}$được đặt vào trong một chiếc cốc có dạng hình trụ với đường kính đáy là 6 cm như hình vẽ. Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến hàng phần trăm).
A. 2,21 cm. B. 2,38 cm. C. 4,52 cm. D. 6,65 cm. |
Lời giải chi tiết
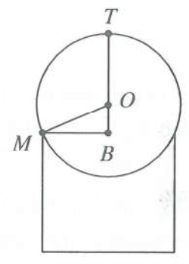
Yêu cầu bài toán $\Leftrightarrow {{h}_{0}}=TB$ (hình vẽ bên)
Thể tích khối cầu là $V=\frac{4}{3}\pi {{R}^{3}}=\frac{256\pi }{3}\Leftrightarrow R=4cm$
Bán kính đáy của hình trụ là $r=\frac{d}{2}=3cm$
Tam giác MBO vuông tại B, có $OB=\sqrt{O{{M}^{2}}-B{{M}^{2}}}=\sqrt{7}$
Do đó $TB=TO+OB=4+\sqrt{7}\approx 6,65cm.$Chọn D.
| Bài tập 4: Cho mặt cầu (S) có bán kính R không đổi (cho trước). Một hình trụ có chiều cao h và bán kính r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. $h=R\sqrt{2}.$ B. $h=R$ C. $h=2R$ D. $h=\frac{R}{2}$ |
Lời giải chi tiết
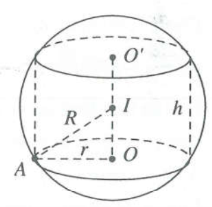
Gọi I là trung điểm $O{O}'\Rightarrow I$ là tâm mặt cầu
Tam giác IAO có ${{r}^{2}}={{R}^{2}}-\frac{{{h}^{2}}}{4}=\frac{1}{2}\sqrt{4{{R}^{2}}-{{h}^{2}}}$
Ta có ${{S}_{xq}}=2\pi Rh=\pi h.\sqrt{4{{\text{R}}^{2}}-{{h}^{2}}}$
$=\pi \sqrt{\underbrace{{{h}^{2}}}_{a}.\underbrace{\left( 4{{\text{R}}^{2}}-{{h}^{2}} \right)}_{b}}\overset{Co-si}{\mathop{\le }}\,\pi .\frac{{{h}^{2}}+\left( 4{{\text{R}}^{2}}-{{h}^{2}} \right)}{2}$
Suy ra ${{S}_{xq}}\le 2\pi {{R}^{2}}\xrightarrow{{}}{{S}_{ma\text{x}}}=2\pi {{R}^{2}}.$
Dấu bằng xảy ra khi ${{h}^{2}}=4{{\text{R}}^{2}}-{{h}^{2}}\Leftrightarrow $$h=R\sqrt{2}$. Chọn A.
| Bài tập 5: Cho mặt cầu (S) có bán kính R không đổi (cho trước). Một hình trụ có chiều cao h và bán kính r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho thể tích khối trụ lớn nhất.
A. $h=\frac{R\sqrt{2}}{2}.$ B. $h=\frac{2R\sqrt{3}}{3}.$ C. $h=\frac{R\sqrt{3}}{2}.$ D. $h=R\sqrt{2}.$ |
Lời giải chi tiết
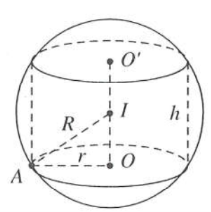
Gọi I là trung điểm $O{O}'\Rightarrow I$ là tâm mặt cầu
Tam giác IAO có ${{r}^{2}}={{\text{R}}^{2}}-\frac{{{h}^{2}}}{4}=\frac{1}{2}\sqrt{4{{\text{R}}^{2}}-{{h}^{2}}}$
Ta có $V=\pi {{r}^{2}}h=\pi h.\left( {{\text{R}}^{2}}-\frac{{{h}^{2}}}{4} \right)=f\left( h \right)$
Xét hàm số $f\left( h \right)$có ${f}'\left( h \right)=\pi {{\text{R}}^{2}}-\frac{3\pi }{4}{{h}^{2}}=0\Leftrightarrow $$h=\frac{2R\sqrt{3}}{3}.$
Lập bảng biến thiên $\Rightarrow {{V}_{max}}$ khi $h=\frac{2R\sqrt{3}}{3}.$ Chọn B.
TOÁN LỚP 12