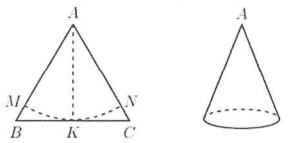
Bài tập liên quan đến công thức diện tích, thể tích mặt nón hình nón khối nón có đáp án chi tiết

Bài tập liên quan đến công thức diện tích, thể tích mặt nón hình nón khối nón có đáp án
Dưới đây là bài tập trắc nghiệm liên quan đến công thức diện tích và thể tích của các hình nón có đáp án chi tiết
| Bài tập 1: Diện tích xung quanh hình nón có bán kính đáy R = 3, chiều cao h = 4 bằng
A. 12$\pi $ B. $6\pi $ C. $15\pi $ D. $9\pi $ |
Lời giải chi tiết
Độ dài đường sinh $l=\sqrt{{{R}^{2}}+{{h}^{2}}}=\sqrt{{{3}^{2}}+{{4}^{2}}}=5$
Vậy diện tích xung quanh hình nón là ${{S}_{xq}}=\pi Rl=15\pi $. Chọn C
| Bài tập 2: Cho hình nón (N) có bán kính đáy bằng 4, diện tích xung quanh bằng 20$\pi $. Thể tích khối nón đã cho bằng
A. $4\pi $ B. $8\pi $ C. $20\pi $ D. $16\pi $ |
Lời giải chi tiết
Theo giả thiết, ta có $\left\{ \begin{array} {} R=4 \\ {} {{S}_{xq}}=20\pi \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} R=4 \\ {} \pi Rl=20\pi \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} R=4 \\ {} l=5 \\ \end{array} \right.$
Lại có: ${{l}^{2}}={{h}^{2}}+{{R}^{2}}\to h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\sqrt{{{5}^{2}}-{{4}^{2}}=3}$
Vậy thể tích khối nón (N) là ${{V}_{\left( N \right)}}=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}{{.4}^{2}}.3=16\pi $
Chọn D
| Bài tập 3: Cho hình nón (N) có diện tích xung quanh bằng $2\pi $, diện tích toàn phần bằng $3\pi $. Thể tích khối nón đã cho bằng
A. $\frac{\sqrt{3}}{3}\pi $ B. $\frac{\sqrt{3}}{6}\pi $ C. $\frac{\sqrt{6}}{6}\pi $ D. $\frac{\sqrt{3}}{2}\pi $ |
Lời giải chi tiết
Diện tích xung quanh hình nón là ${{S}_{xq}}=\pi Rl=2\pi \leftrightarrow Rl=2$
Diện tích toàn phần hình nón là ${{S}_{tp}}=\pi Rl+\pi {{R}^{2}}=3\pi \leftrightarrow Rl+{{R}^{2}}=3$
Do đó $\left\{ \begin{array} {} Rl=2 \\ {} Rl+{{R}^{2}}=3 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} {{R}^{2}}=1 \\ {} Rl=2 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} R=1 \\ {} l=2 \\ \end{array} \right.\to h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\sqrt{3}$
Vậy thể tích khối nón (N) là ${{V}_{\left( N \right)}}=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}{{.1}^{2}}.\sqrt{3}=\frac{\sqrt{3}}{3}\pi $
Chọn A
| Bài tập 4: Cho hình nón (N) có góc ở đỉnh bằng 60°, độ dài đường sinh bằng 4. Thể tích khối nón đã cho bằng
A. $\frac{4\sqrt{3}\pi }{3}$ B. $\frac{8\sqrt{3}\pi }{3}$ C. $2\sqrt{3}\pi $ D. $\frac{\sqrt{3}\pi }{2}$ |
Lời giải chi tiết
Vì góc ở đỉnh của hình nón bằng 60° $l=2R=4\Rightarrow R=2$
Ta có ${{h}^{2}}+{{R}^{2}}={{l}^{2}}\Rightarrow h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\sqrt{{{4}^{2}}-{{2}^{2}}}=2\sqrt{3}$
Vậy thể tích khối nón đã cho là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{.2}^{2}}.2\sqrt{3}=\frac{8\sqrt{3}\pi }{3}$.
Chọn B.
| Bài tập 5: Trong không gian, cho tam giác AC vuông tại A, AB = a và AC = a$\sqrt{3}$. Độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng
A. $l=a$ B. $l=a\sqrt{2}$ C. $l=a\sqrt{3}$ D. $l=2a$ |
Lời giải chi tiết
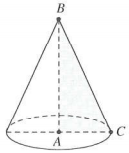
Kỹ năng vẽ hình: Tam giác quay quanh cạnh nào thì cạnh đó là trục, động thời chính là chiều cao của hình nón
Quay tam giác ABC xung quanh trục AB, ta được hình nón có chiều cao h = AB = a, bán kính đáy $R=AC=a\sqrt{3}$ (hình vẽ bên)
Do đó, độ dài đường sinh là $l=\sqrt{{{h}^{2}}+{{R}^{2}}}=2a$.
Chọn D.
| Bài tập 6: Trong không gian, cho tam giác ABC vuông tại A, góc ABC = 60°, BC = 4a. Thể tích khối nón nhận được khi quay tam giác ABC xung quanh trục AC bằng
A. $\frac{4\sqrt{3}\pi {{a}^{3}}}{3}$ B. $\frac{8\sqrt{3}\pi {{a}^{3}}}{3}$ C. $\frac{8\sqrt{3}\pi {{a}^{3}}}{9}$ D. $\frac{4\sqrt{3}\pi {{a}^{3}}}{9}$ |
Lời giải chi tiết
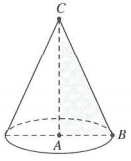
Tam giác ABC vuông tại A, có $\sin A\hat{B}C=\frac{AC}{BC}\Rightarrow AC=2a\sqrt{3}$
Và $AB=\sqrt{B{{C}^{2}}-A{{C}^{2}}}=\sqrt{{{\left( 4a \right)}^{2}}-{{\left( 2a\sqrt{3} \right)}^{2}}}=2a$
Quay tam giác ABC xung quanh trục AC, ta được hình nón có chiều cao $h=AC=2a\sqrt{3}$, bán kính đáy $R=AB=2a$ (hình vẽ bên)
Vậy thể tích khối nón cần tìm là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{8\sqrt{3}\pi {{a}^{3}}}{3}$
Chọn B
| Bài tập 7: Trong không gian, cho tam giác ABC đều cạnh 2a. Gọi H là trung điểm của BC. Thể tích của khối nón nhận được khi quay tam giác ABC xung quanh trục AH bằng
A. $\frac{\sqrt{3}\pi {{a}^{3}}}{9}$ B. $\frac{\sqrt{3}\pi {{a}^{3}}}{2}$ C. $\frac{\sqrt{3}\pi {{a}^{3}}}{3}$ D. $\frac{\sqrt{3}\pi {{a}^{3}}}{6}$ |
Lời giải chi tiết
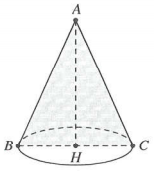
Quay tam giác ABC quanh trục AH, ta được hình nón có chiều cao $h=AH=a\sqrt{3}$, bán kính đáy $R=BH=\frac{BC}{2}=a$(hình vẽ bên)
Vậy thể tích khối nón cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\sqrt{3}\pi {{a}^{3}}}{3}$
Chọn C
| Bài tập 8: Trong không gian, cho tam giác ABC vuông tại A, AB = 3a, BC = 5a. Thể tích khối tròn xoay nhận được khi quay tam giác ABC xung quanh trục BC bằng
A. $\frac{36\pi {{a}^{3}}}{5}$ B. $\frac{48\pi {{a}^{3}}}{25}$ C. $\frac{16\pi {{a}^{3}}}{5}$ D. $\frac{48\pi {{a}^{3}}}{5}$ |
Lời giải chi tiết
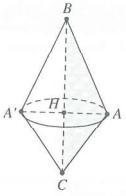
Gọi H là hình chiếu vuông góc của A trên BC
Tam giác ABC vuông tại A, có $AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=4a$
Suy ra $\frac{1}{A{{H}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{C}^{2}}}=\frac{1}{{{\left( 3a \right)}^{2}}}+\frac{1}{{{\left( 4a \right)}^{2}}}\Rightarrow AH=\frac{12a}{5}$
Quay tam giác ABC quanh trục BC, ta được hai hình nón có chiều cao lần lượt là ${{h}_{1}}=BH,{{h}_{2}}=CH$ và bán kính đáy R = AH (hình vẽ bên)
Vậy thể tích khối tròn xoay cần tính là $V={{V}_{1}}+{{V}_{2}}$
$=\frac{1}{3}\pi {{R}^{2}}{{h}_{1}}+\frac{1}{3}\pi {{R}^{2}}{{h}_{2}}=\frac{1}{3}\pi {{R}^{2}}\left( {{h}_{1}}+{{h}_{2}} \right)=\frac{1}{3}\pi .A{{H}^{2}}.BC=\frac{48\pi {{a}^{3}}}{5}$
Chọn D.
| Bài tập 9: Trong không gian, cho hình thang ABCD vuông tại A và D, AB = AD = a, CD = 2a. Thể tích khối tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AD bằng
A. $\frac{7\pi {{a}^{3}}}{3}$ B. $\frac{5\pi {{a}^{3}}}{3}$ C. $\frac{4\pi {{a}^{3}}}{3}$ D. $\frac{8\pi {{a}^{3}}}{3}$ |
Lời giải chi tiết
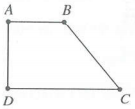
Quay hình thang ABCD quanh trục AD, ta được khối nón cụt có hai bán kính đáy lần lượt là ${{R}_{1}}=AB,{{R}_{2}}=CD$và chiều cao h = AD
Công thức tính thể tích nón cụt $$ được phát triển từ công thức thể tích tổng quát của khối có hai đáy song song
Vậy thể tích cần tính là $V=\frac{1}{3}\pi a.\left[ {{a}^{2}}+{{\left( 2a \right)}^{2}}+a.2a \right]=\frac{7\pi {{a}^{3}}}{3}$
Chọn A.
| Bài tập 10: Trong không gian, cho hình thang ABCD có AB//CD và AB = AD = BC =a, CD = 2a. Thể tích khối tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AB bằng
A. $\frac{5\pi {{a}^{3}}}{3}$ B. $\pi {{a}^{3}}$ C. $\frac{5\pi {{a}^{3}}}{4}$ D. $\frac{5\pi {{a}^{3}}}{2}$ |
Lời giải chi tiết
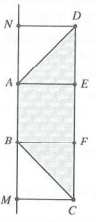
Thể tích khối tròn xoay khi quay hình thang ABCD quanh trục AB ta được khối tròn xoay có thể tích V tạo bởi hai khối:
l Khối trụ tròn xoay có chiều cao h = CD = MN =2a và bán kính đường tròn đáy $R=DN=\sqrt{D{{A}^{2}}-N{{A}^{2}}}=\frac{a\sqrt{3}}{2}$( như hình vẽ bên ).
l Thể tích khối trụ trên trừ đi thể tích 2.V2 của hai khối nón có chiều cao ${{h}_{2}}=\frac{a}{2}$và bán kính đường tròn đáy $R=DN=\frac{a\sqrt{3}}{2}$.
Vậy thể tích khối tròn xoay cần tính là $V={{V}_{1}}-2.{{V}_{2}}=\pi .2a.\frac{3{{a}^{2}}}{4}-\frac{2}{3}.\pi .\frac{a}{2}.\frac{3{{a}^{2}}}{4}=\frac{5}{4}\pi {{a}^{3}}$
Chọn C
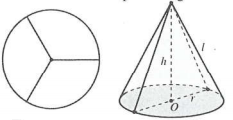
| Bài tập 11: Người thợ gia công của một cơ sở chất lượng cao X cắt một miêng tôn hình tròn với bán kính 60 cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miệng tôn đó để được ba cái phễu hình nón. Thể tích của mỗi cái phễu bằng
A. $\frac{8\sqrt{2}\pi }{3}$lít B. $\frac{16\sqrt{2}\pi }{3}$lít C. $\frac{1600\sqrt{2}\pi }{3}$lít D. $\frac{32\sqrt{2}\pi }{3}$lít |
Lời giải chi tiết
Khi quấn hình quạt để tạo thành một hình nón, ta được
l Đường sinh hình nón bằng bán kính hình quạt $l=R=60cm$
l Chu vi đáy hình nón bằng độ dài cung hình quạt $C=2\pi r=\frac{1}{3}.2\pi .60\Rightarrow r=20$
Do đó, chiều cao của hình nón là $h=\sqrt{{{l}^{2}}-{{r}^{2}}}=\sqrt{{{60}^{2}}-{{20}^{2}}}=40\sqrt{2}cm$
Vậy thể tích của mỗi cái phễu là $V=\frac{1}{3}\pi {{r}^{2}}h=\frac{1}{3}\pi {{.20}^{2}}.40\sqrt{2}=\frac{1600\sqrt{2}\pi }{3}c{{m}^{2}}=\frac{16\sqrt{2}\pi }{3}$lít.
Chọn B.
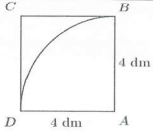
| Bài tập 12: Có một miếng tôn hình tam giác đều ABC cạnh 3 dm (như hình vẽ).
Gọi K là trung điểm của BC. Người ta dùng compa có tâm là A và bán kính AK vạch ra cung tròn MN (M, N theo thứ tự thuộc cạnh AB và AC) rồi cắt miếng tôn theo cung tròn đó. Lấy phần hình quạt người ta gò sao cho cạnh AM và AN' trùng nhau thành một cái phếu hình nón không đáy với đỉnh A. Tính thể tích V của cái phễu. A. $V=\frac{\sqrt{141}.\pi }{64}d{{m}^{3}}$ B. $V=\frac{\sqrt{105}.\pi }{64}d{{m}^{3}}$ C. $V=\frac{3\sqrt{3}.\pi }{32}d{{m}^{3}}$ D. $V=\frac{3\pi }{64}d{{m}^{3}}$ |
Lời giải chi tiết
Độ dài đường sinh của phễu là ${{l}_{N}}=AM=AK=\frac{3\sqrt{3}}{2}$
Độ dài cung MN là $\ell =\frac{60}{360}.2\pi .AK=\frac{1}{3}\pi .\frac{3\sqrt{3}}{2}=\frac{\sqrt{3}\pi }{2}\left( dm \right)$
Bán kính đáy của phễu là $r=\frac{\ell }{2\pi }=\frac{\sqrt{3}}{4}$ suy ra $V=\frac{1}{3}\pi {{r}^{2}}h=\frac{1}{3}\pi {{r}^{2}}.\sqrt{\ell _{N}^{2}-{{r}^{2}}}=\frac{\sqrt{105}\pi }{64}\left( d{{m}^{3}} \right)$
Chọn B.
| Bài tập 13: Từ miếng tôn hình vuông cạnh bằng 4 dm, người ta cắt ra hình quạt tâm A bán kính AB = AD = 4 dm (xem hình) để cuộn lại thành một chiếc phễu hình nón (khi đó AB trùng với AD). Chiều cao của chiếc phễu có số đo gần đúng (làm tròn đến 3 chữ số thập phân) là
A. 3,872 dm B. 3,874 dm C. 3,871 dm D. 3,873 dm |
Lời giải chi tiết
Chu vi của đáy hình nón có độ dài bằng cung BD.
Độ dài cung BDlà: $l=\frac{1}{4}.\left( 2\pi .4 \right)=2\pi $. Suy ra bán kính đường tròn đáy hình nón là : $r=\frac{2\pi }{2\pi }=1$
Độ dài đường sinh của hình nón là $\ell =4dm\Rightarrow h=\sqrt{{{\ell }^{2}}-{{r}^{2}}}=3,873dm$.
Chọn D.
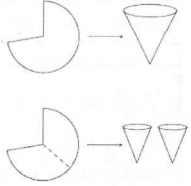
| Bài tập 14: Từ một tấm kim loại dẻo hình quạt (như hình vẽ) có bán kính R= 13 và chu vi hình quạt là $P=12\pi $, người ta gò tấm kim loại đó thành những chiếc phễu hình nón theo hai cách:
Cách 1: Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu. Cách 2: Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung quanh của hai cái phễu. Gọi V1 là thể tích của cái phễu ở cách 1, V2 là tổng thể tích của hai cái phễu ở cách 2. Tính tỉ số $\frac{{{V}_{1}}}{{{V}_{2}}}$
A. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\sqrt{133}}{\sqrt{160}}$ B. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{2\sqrt{133}}{\sqrt{160}}$ C. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{2\sqrt{160}}{\sqrt{133}}$ D. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\sqrt{5}}{2}$ |
Lời giải chi tiết
Theo cách 1 ta có: Độ dài đường sinh của hình nón là: $\ell =13$, chu vi đáy $r=\frac{12\pi }{2\pi }=6$
Khi đó thể tích của chiếc phễu là: ${{V}_{1}}=\frac{1}{3}\pi {{r}^{2}}\sqrt{{{\ell }^{2}}-{{h}^{2}}}=12\pi \sqrt{133}$
Theo cách 2 ta có: Độ dài đường sinh của hình nón là: $\ell =13$, chu vi đáy mỗi phễu là: $r=\frac{6\pi }{2\pi r}\Rightarrow r=3$
Khi đó tổng thể tích của hai chiếc phễu là: ${{V}_{2}}=\frac{2}{3}\pi {{r}^{2}}\sqrt{{{\ell }^{2}}-{{h}^{2}}}=24\pi \sqrt{10}$
Quy ra $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\sqrt{133}}{2\sqrt{10}}=\frac{2\sqrt{133}}{\sqrt{160}}$
Chọn D.
| Bài tập 15: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng $\frac{1}{3}$ chiều cao của phễu. Hỏi nêu bịt kín miệng phễu rồi lộn ngược phễu lên thì chiều cao nước xấp xỉ bằng bao nhiêu? Biết rằng chiều cao của phễu là 15 cm
A. 0,5 cm B. 0,3 cm C. 0,188 cm D. 0,216 cm |
Lời giải chi tiết
Gọi bán kính đáy của phễu là R, chiều cao của phễu là h = l5 em
Vì chiều cao nước trong phễu ban đầu bằng $\frac{1}{3}h$
Suy ra bán kính đáy hình nón tạo bởi lượng nước là $\frac{1}{3}R$
Thể tích phễu và thể tích nước lần lượt là $V=\frac{1}{3}\pi {{R}^{2}}h=5\pi {{R}^{2}},{{V}_{1}}=\frac{1}{3}\pi {{\left( \frac{R}{3} \right)}^{2}}.\frac{h}{3}=\frac{5}{27}\pi {{R}^{2}}$
Do đó, thể tích phần khối nón không chứa nước là ${{V}_{2}}=V-{{V}_{1}}=5\pi {{R}^{2}}-\frac{5}{27}\pi {{R}^{2}}=\frac{130}{27}\pi {{R}^{2}}\Rightarrow \frac{{{V}_{2}}}{V}=\frac{26}{27}$
Gọi h’ và r lần lượt là chiều cao và bán kính đáy của khối nón không chứa nước
$\frac{h'}{h}=\frac{r}{R}\Rightarrow \frac{{{V}_{2}}}{V}=\frac{h{{'}^{3}}}{{{h}^{3}}}=\frac{h{{'}^{3}}}{{{15}^{3}}}=\frac{26}{27}\to h'=5\sqrt[3]{26}$
Vậy chiều cao cần tính là ${{h}_{o}}=h-h'=15-5\sqrt[3]{26}=0,188cm$
Chọn C.
| Bài tập 16: Bạn Hùng có một tấm bìa hình tròn như vẽ bên dưới, Hùng muốn biến hình tròn đó thành một cái phễu hình nón. Khi đó bạn Hùng phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt dùng làm phễu. Tìm x để thể tích phễu lớn nhất?
A. $\frac{2\sqrt{3}\pi }{3}$ B. $\frac{2\sqrt{6}\pi }{3}$ C. $\frac{\sqrt{3}\pi }{2}$ D. $\frac{\sqrt{3}\pi }{6}$ |
Lời giải chi tiết
Gọi R, h lần lượt là bán kính đáy, chiều cao của hình nón
Thể tích khối nón là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}{{R}^{2}}.\sqrt{{{l}^{2}}-{{R}^{2}}}$
Ta có: ${{R}^{4}}\left( {{l}^{2}}-{{R}^{2}} \right)=4.\frac{{{R}^{2}}}{2}.\frac{{{R}^{2}}}{2}.\left( {{l}^{2}}-{{R}^{2}} \right)\le 4.\frac{{{\left( \frac{{{R}^{2}}}{2}+\frac{{{R}^{2}}}{2}+{{l}^{2}}-{{R}^{2}} \right)}^{3}}}{27}=\frac{4{{l}^{6}}}{27}$
Do đó ${{R}^{2}}.\left( {{l}^{2}}-{{R}^{2}} \right)\le \sqrt{\frac{4{{l}^{6}}}{27}}=\frac{2\sqrt{3}{{l}^{3}}}{9}\Rightarrow V\le \frac{2\sqrt{3}\pi {{l}^{3}}}{27}$
Dấu bằng xảy ra khi$\frac{{{R}^{2}}}{2}={{l}^{2}}-{{R}^{2}}\Leftrightarrow {{l}^{2}}=\frac{3}{2}{{R}^{2}}\Leftrightarrow l=\frac{R\sqrt{6}}{2}$ (1)
Hình nón nhận được là có đường sinh l = OA, chu vi đáy là độ dài cung AB
Vì $x=\widehat{AOB}\Rightarrow $độ dài cung $AB=OA\times x=lx\Rightarrow 2\pi R=lx\Rightarrow x=\frac{2\pi R}{l}$ (2)
Từ (1), (2) suy ra $x=2\pi .\frac{R}{l}=2\pi .\frac{2}{\sqrt{6}}=\frac{2\sqrt{6}\pi }{3}$.
Chọn B.
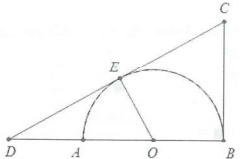
| Bài tập 17: Cho nửa đường tròn đường kính AB = 2R, kí hiệu A là đường thắng vuông góc với AB tại B. Trên nửa đường tròn lấy điểm E di động, tiếp tuyến của nửa đường tròn tại E và cắt tia đối của tia AB tại D và cắt ∆ tại C (như hình vẽ dưới). Khi quay tam giác BCD quanh trục AB ta được khối tròn xoay có thể tích nhỏ nhất là ?
A. $\frac{8\pi {{R}^{3}}}{27}$ B. $\frac{8\sqrt{3}\pi {{R}^{3}}}{9}$ C. $\frac{8\pi {{R}^{3}}}{3}$ D. $\frac{8\pi {{R}^{3}}}{9}$. |
Lời giải chi tiết
Đặt $\widehat{BOC}=\alpha \Rightarrow \alpha \in \left( {{45}^{o}};{{90}^{o}} \right)\Rightarrow \tan \alpha >1$, chú ý công thức tan sau $\tan 2\alpha =\frac{2\tan \alpha }{1-{{\tan }^{2}}\alpha }$
Tam giác OBC vuông tại B, có $\tan \widehat{BOC}=\frac{BC}{BO}\Rightarrow BC=R.\tan \alpha $
Ta có $\widehat{BCD}=2\left( {{90}^{o}}-\alpha \right)\Rightarrow BD=BC.\tan \left( {{180}^{o}}-2\alpha \right)=-BC.\tan 2\alpha $.
Khi quay tam giác BCD quanh trục AB ta được khối tròn xoay có thể tích là
$V=\frac{1}{3}\pi {{r}^{2}}h-\frac{\pi }{3}.B{{C}^{2}}.BD=-\frac{\pi }{3}.B{{C}^{2}}.\tan 2\alpha =\frac{2\pi }{3}.{{R}^{3}}.\frac{{{\tan }^{4}}\alpha }{{{\tan }^{2}}\alpha -1}\ge \frac{8\pi {{R}^{3}}}{3}$
Vì ${{\tan }^{4}}\alpha \ge 4\left( {{\tan }^{2}}\alpha -1 \right)\Leftrightarrow {{\left( {{\tan }^{2}}\alpha -2 \right)}^{2}}\ge 0;\forall \alpha \in \left( {{45}^{o}};{{90}^{o}} \right)$. Vậy ${{V}_{\min }}=\frac{8\pi {{R}^{3}}}{3}$
Chọn C.
TOÁN LỚP 12