Bài tập Hình nón nội — ngoại tiếp khối chóp đều

Bài tập Hình nón nội — ngoại tiếp khối chóp đều

Mô hình	Hình vẽ tham khảo (3D)	Tính chất
Hình nón nội tiếp hình chóp tam giác đều		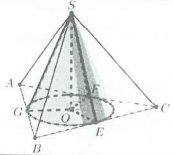l        Chiều cao SO là chiều cao của hình chóp l        Bán kính đáy OE là bán kính đường tròn nội tiếp tam giác đáy l        Đường sinh $l=SE$
Hình nón ngoại tiếp hình chóp tam giác đều		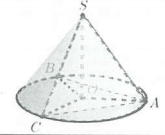l        Chiều cao SO là chiều cao của hình chóp l        Bán kính đáy OA là bán kính đường tròn ngoại tiếp tam giác đáy l        Đường sinh $l=SA$
Hình nón nội tiếp hình chóp tứ giác đều		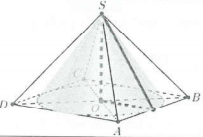l        Chiều cao SO là chiều cao của hình chóp l        Bán kính đáy OM (với M là trung điểm AB) là bán kính đường tròn nội tiếp hình vuông đáy l        Đường sinh $l=SM$
Hình nón ngoại tiếp hình chóp tứ giác đều		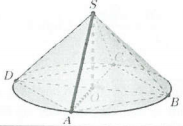l        Chiều cao SO là chiều cao của hình chóp l        Bán kính đáy OA là bán kính đường tròn ngoại tiếp hình vuông đáy l        Đường sinh $l=SA$

Lời giải chi tiết

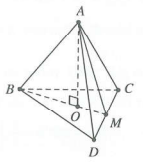
Gọi O là tâm đường tròn ngoại tiếp  ∆BCD $\Rightarrow AO\bot \left( BCD \right)$

Dễ thấy, bán kính đường tròn ngoại tiếp ∆BCD  là $OB=\frac{a\sqrt{3}}{3}$

Suy ra bán kính đáy hình nón là $R=\frac{a\sqrt{3}}{3}$

Tam giác ABO vuông tại O, có $AO=\sqrt{A{{B}^{2}}-O{{B}^{2}}}=\frac{a\sqrt{6}}{3}$

Do đó, chiều cao của hình nón là $h=AO=\frac{a\sqrt{6}}{3}$

Vậy thể tích cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi .{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}.\frac{a\sqrt{6}}{3}=\frac{\sqrt{6}\pi {{a}^{3}}}{27}$

Chọn C

Lời giải chi tiết

Theo bài ra, ta có bán kính đáy $R=\frac{a\sqrt{2}}{2}$; đường sinh $l=4a$(xem mô hình ở lý thuyết)

Vậy diện tích xung quanh cần tính là ${{S}_{xq}}=\pi Rl=\pi .\frac{a\sqrt{2}}{2}.4a=2\sqrt{2}\pi {{a}^{2}}$. Chọn A.

Lời giải chi tiết

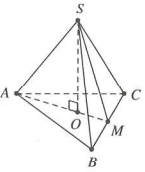
Gọi O là tâm đường tròn ngoại tiếp  ∆ABC $\Rightarrow SO\bot \left( ABC \right)$

Bán kính đáy hình nón là $R={{r}_{\Delta ABC}}=OM=\frac{a\sqrt{3}}{6}$

Tam giác SAO vuông tại O, có $SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\frac{a\sqrt{6}}{3}$

Vậy thể tích khối nón cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}.{{\left( \frac{a\sqrt{3}}{6} \right)}^{2}}.\frac{a\sqrt{6}}{3}=\frac{\sqrt{6}\pi {{a}^{3}}}{108}$

 Chọn C.

Lời giải chi tiết

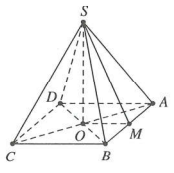
Gọi M là trung điểm AB $\Rightarrow SM\bot AB\Rightarrow {{S}_{\Delta SAB}}=\frac{1}{2}SM.AB$

Mà ${{S}_{\Delta SAB}}=2{{a}^{2}};AB=a\to SM=2.2{{a}^{2}}:a=4a$

Bán kính đáy hình nón $R=OM=\frac{AB}{2}=\frac{a}{2}$

Tam giác SMO vuông tại M, có $SO=\sqrt{S{{M}^{2}}-O{{M}^{2}}}=\frac{3\sqrt{7}a}{2}$

Vậy thể tích khối nón cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}.{{\left( \frac{a}{2} \right)}^{2}}.\frac{3\sqrt{7}a}{{}}=\frac{\pi {{a}^{3}}\sqrt{7}}{8}$

Chọn B.

Lời giải chi tiết

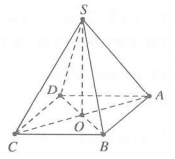
Gọi O là tâm hình vuông ABCD $\Rightarrow $ O là tâm đường tròn ngoại tiếp hình vuông ABCD

Theo bài ra, đáy hình nón là đường tròn ngoại tiếp ABCD

$\Rightarrow R={{R}_{ABCD}}=OA=\frac{AC}{2}=a\Rightarrow AC=2a\Rightarrow AB=a\sqrt{2}$

Diện tích xung quanh hình nón là ${{S}_{xq}}=\pi Rl=2\pi {{a}^{2}}\Rightarrow l=2a$

Hình nón (N) có đường sinh $l=SA=2a$

Tam giác SAO vuông tại O, có  $SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=a\sqrt{3}$

Vậy thể tích khối chóp S.ABCD là ${{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{a\sqrt{3}}{3}.{{\left( a\sqrt{2} \right)}^{2}}=\frac{2\sqrt{3}{{a}^{3}}}{3}$

Chọn D

Lời giải chi tiết

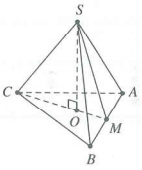
Gọi O là tâm đường tròn ngoại tiếp $\Delta ABC\Rightarrow SO\bot \left( ABC \right)$

Bán kính đáy hình nón là $R={{R}_{\Delta ABC}}=OA=\frac{a\sqrt{3}}{3}$

Gọi M là trung điểm AB $\Rightarrow \left\{ \begin{align}  & AB\bot OM \\  & AB\bot SO \\ \end{align} \right.\Rightarrow AB\bot \left( SMO \right)$

Do đó $\left( \left( SAB \right);\left( ABC \right) \right)=\left( SM;OM \right)=S\hat{M}O={{60}^{o}}$

Tam giác SMO vuông tại O, có $\cos S\hat{M}O=\frac{OM}{SM}\Rightarrow SM=\frac{a\sqrt{3}}{3}$

Tam giác SBM vuông tại M, có $SB=\sqrt{S{{M}^{2}}+B{{M}^{2}}}=\frac{a\sqrt{21}}{6}$

Vậy hình nón có đường sinh $l=\frac{a\sqrt{21}}{6}\to {{S}_{sq}}=\pi Rl=\frac{\sqrt{7}\pi {{a}^{2}}}{6}$

Chọn A.

Lời giải chi tiết

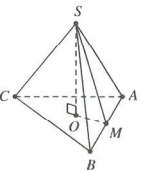
Gọi O là tâm đường tròn nội tiếp ∆ABC $SO\bot \left( ABC \right)$

Kẻ $OM\bot AB\Rightarrow OM$ là bán kính đường tròn nội tiếp ∆ABC

Diện tích ∆ABC là ${{S}_{\Delta ABC}}=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}=48{{a}^{2}}$

Suy ra bán kính đường tròn nội tiếp $\Delta ABC\Rightarrow {{r}_{\Delta ABC}}=\frac{S}{p}=3a$

Ta có $AB\bot \left( SMO \right)\Rightarrow \left( \left( SAB \right);\left( ABC \right) \right)=\widehat{SMO}={{45}^{o}}$

Tam giác SMO vuông tại O, có $SO=OM={{r}_{\Delta ABC}}=3a$

Vậy thể tích khôi nón cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi }{3}.{{\left( 3a \right)}^{2}}.3a=9\pi {{a}^{3}}$

Chọn B.

Lời giải chi tiết

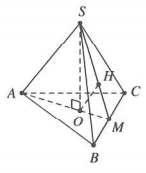
Gọi M là trung điểm BC $\Rightarrow BC\bot AM\Rightarrow BC\bot \left( SAM \right)$

Kẻ $OH\bot SM$ mà $BC\bot OH\Rightarrow OH\bot \left( ABC \right)$

Tacó $OM=\frac{1}{3}AM=\frac{1}{3}.\frac{\sqrt{3}}{2}AB=\frac{1}{3}.\frac{\sqrt{3}}{2}.2a=\frac{a\sqrt{3}}{3}$

Tam giác SMO vuông tại O, có $\frac{1}{O{{H}^{2}}}=\frac{1}{S{{O}^{2}}}+\frac{1}{O{{M}^{2}}}\Rightarrow SO=a$

Bán kính đường tròn ngoại tiếp $\Delta ABC$ là ${{R}_{\Delta ABC}}=\frac{2a\sqrt{3}}{3}$

Vậy thể tích khối nón cần tính là $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{\pi a}{3}.{{\left( \frac{2a\sqrt{3}}{3} \right)}^{2}}=\frac{4\pi {{a}^{3}}}{9}$

Chọn C