Bài tập đồ thị dao động điều hòa có đáp án chi tiết

BÀI TẬP VỀ ĐỒ THỊ DAO ĐỘNG ĐIỀU HÒA CÓ LỜI GIẢI CHI TIẾT:
|
|
Lời giải chi tiết
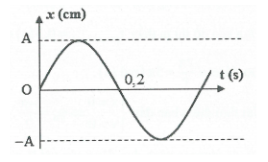
Dựa vào đồ thị ta thấy khoảng thời gian 2 lần liên tiếp vật có li độ x = 0 là:
$\frac{T}{2}=0,2\Rightarrow T=0,4s\Rightarrow \omega =\frac{2\pi }{T}=5s\left( rad/s \right)$. Chọn C
|
|
Lời giải chi tiết
Từ đồ thị ta thấy rằng $\left\{ \begin{array}{} {{x}_{0}}=\frac{A}{2}=2\text{ }(cm) \\ {} {{v}_{0}}<0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=\frac{\pi }{3}$
Lại có: ${{t}_{\left( 2\to 0\to -4 \right)}}={{t}_{\left( \frac{A}{2}\to 0\to -A \right)}}=0,4s\Rightarrow \frac{T}{12}+\frac{T}{4}=0,4\Rightarrow T=1,2s\Rightarrow \omega =\frac{2\pi }{T}=\frac{5\pi }{3}$
Vậy phương trình dao động của vật là: $x=4\cos \left( \frac{5\pi t}{3}+\frac{\pi }{3} \right)\text{ (cm)}$. Chọn A
|
|
Lời giải chi tiết
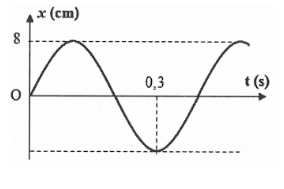
Biên độ dao động của vật là A = 8 (cm)
Dựa vào đồ thị ta thấy ${{t}_{\left( 0\to A\to -A \right)}}=0,3(s)\Leftrightarrow \frac{3T}{4}=0,3\Rightarrow T=0,4\left( s \right)$
Do đó $\omega =\frac{2\pi }{T}=5\pi \left( rad/s \right)$
Tại thời điểm ban đầu $\left\{ \begin{array}{} x=0 \\ {} v>0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=\frac{-\pi }{2}$
Do đó phương trình dao động của vật là: $x=8\cos \left( 5\pi -\frac{\pi }{2} \right)\text{ }\left( cm \right)$. Chọn C
|
A.$v=60\pi \cos \left( 10\pi t-\frac{\pi }{3} \right)\text{ }\left( cm/s \right)$ B. $v=60\pi \cos \left( 10\pi t-\frac{\pi }{6} \right)\text{ }\left( cm/s \right)$ C. $v=60\cos \left( 10\pi t-\frac{\pi }{3} \right)\text{ }\left( cm/s \right)$ D.$v=60\cos \left( 10\pi t-\frac{\pi }{6} \right)\text{ }\left( cm/s \right)$ |
Lời giải chi tiết
Biên độ dao động của vật là A = 6 (cm)
Dựa vào đồ thị ta thấy rằng sau 0,2s trạng thái dao động vật được lặp lại, do đó $T=0,2s\Rightarrow \omega =\frac{2\pi }{T}=10\pi \left( rad/s \right)$
Tại thời điểm bạn đầu $\left\{ \begin{array}{} x=-3cm=\frac{-A}{2} \\ {} v>0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=\frac{-2\pi }{3}$
Do đó phương trình dao động của vật là $x=6\cos \left( 10\pi t-\frac{2\pi }{3} \right)cm$
$\Rightarrow v=60\pi \cos \left( 10\pi t-\frac{2\pi }{3}+\frac{\pi }{2} \right)=60\pi \cos \left( 10\pi t-\frac{\pi }{6} \right)\left( cm/s \right)$. Chọn B
|
A. $x=3\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm$ B. $x=3\cos \left( 4\pi t-\frac{5\pi }{6} \right)cm$ C.$x=4\cos \left( 3\pi t-\frac{\pi }{3} \right)cm$ D. $x=4\cos \left( 3\pi t-\frac{5\pi }{6} \right)cm$ |
Lời giải chi tiết
Ta có: ${{v}_{\max }}=\omega A=12\pi ;{{v}_{0}}=6\pi \sqrt{3}$
Lại có: $\begin{array}{} \Rightarrow T=0,5\,s\Rightarrow \omega =\frac{2\pi }{T}=4\pi \,(rad/s). \\ {} x=-4 \\ {} t=5s \\ \end{array}$
$\Rightarrow T=0,5\,s\Rightarrow \omega =\frac{2\pi }{T}=4\pi \,(rad/s).$
Khi đó $A=\frac{{{v}_{\max }}}{\omega }=3\left( cm \right)$
Tại thời điểm ban đầu $a>0\Rightarrow x=-{{\omega }^{2}}a<0\Rightarrow \left\{ \begin{array}{} x=\frac{-A}{2} \\ {} v>0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=\frac{-2\pi }{3}$
Do đó phương trình dao động của vật là $x=3\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm$. Chọn A
Cách 2: Tại thời điểm ban đầu $\left\{ \begin{array}{} v=6\pi \sqrt{3} \\ {} v\uparrow \\ \end{array} \right.\Rightarrow {{\varphi }_{0v}}=-\frac{\pi }{6}\Rightarrow {{\varphi }_{0x}}=-\frac{\pi }{6}-\frac{\pi }{2}=-\frac{2\pi }{3}$
Do đó phương trình dao động của vật là $x=3\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm$. Chọn A
|
Bài tập 6: Một chất điểm dao động điều hòa dọc theo trục Ox. Đường biểu diễn sự phụ thuộc vận tốc chất điểm theo thời gian t cho ở hình vẽ. Phương trình dao động của chất điểm là: B. $x=2,5cos\left( 8\pi t-\frac{5\pi }{6} \right)cm$ C. $x=2,5cos\left( 8\pi t+\frac{\pi }{6} \right)cm$ D.$x=2,5cos\left( 8\pi t-\frac{\pi }{6} \right)cm$ |
Lời giải chi tiết
Ta có: ${{v}_{\max }}=\omega A=20\pi ;{{v}_{0}}=10\pi $
Lại có: ${{t}_{\left( \frac{{{v}_{\max }}}{2}\to 0\to {{v}_{\max }} \right)}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to A\to 0 \right)}}=\frac{T}{12}+\frac{T}{4}=\frac{1}{12}\Rightarrow T=0,25s\Rightarrow \omega =\frac{2\pi }{T}=8\pi \left( rad/s \right)$
Khi đó $A=\frac{{{v}_{\max }}}{\omega }=2,5\left( cm \right)$
Tại thời điểm ban đầu $a<0\Rightarrow x=-{{\omega }^{2}}a>0\Rightarrow \left\{ \begin{array}{} x=\frac{A\sqrt{3}}{2} \\ {} v>0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=\frac{-\pi }{6}$
Do đó phương trình dao động của vật là $x=2,5\cos \left( 8\pi t-\frac{\pi }{6} \right)cm$. Chọn D
Cách 2: Tại thời điểm ban đầu $\left\{ \begin{array}{} v=10\pi \\ {} v\downarrow \\ \end{array} \right.\Rightarrow {{\varphi }_{0v}}=\frac{\pi }{3}\Rightarrow {{\varphi }_{0x}}=\frac{\pi }{3}-\frac{\pi }{2}=-\frac{\pi }{6}$
Do đó phương trình dao động của vật là $x=2,5\cos \left( 8\pi t-\frac{\pi }{6} \right)cm$. Chọn D
|
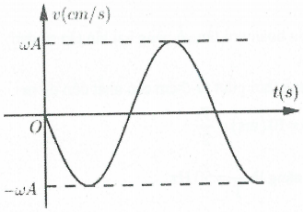
Bài tập 7:[Trích đề thi THPTQG năm 2017]. Hình bên là đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là: B. $x=\frac{3}{4\pi }\cos \left( \frac{20\pi }{3}t+\frac{\pi }{6} \right)\left( cm \right)$ C.$x=\frac{3}{8\pi }\cos \left( \frac{20\pi }{3}t-\frac{\pi }{6} \right)\left( cm \right)$ D.$x=\frac{3}{4\pi }\cos \left( \frac{20\pi }{3}t-\frac{\pi }{6} \right)\left( cm \right)$ |
Lời giải chi tiết
Dựa vào đồ thị ta thấy mỗi ô tính theo trục Ot ứng với thời gian là: $\frac{0,1}{4}=0,025s$
Khoảng thời gian 2 lần liên tiếp vận tốc của vật bằng 0 là $\frac{T}{2}=0,025.6\Rightarrow T=0,3s$
Suy ra $\omega =\frac{2\pi }{T}=\frac{20\pi }{3}$. Tại thời điểm $t=0\Rightarrow \left\{ \begin{array}{} v=\frac{{{v}_{\max }}}{2} \\ {} v\downarrow \\ \end{array} \right.\Rightarrow {{\varphi }_{0v}}=\frac{\pi }{3}$
Do đó phương trình vận tốc là $v=5\cos \left( \frac{20\pi t}{3}+\frac{\pi }{3} \right)\left( cm/s \right)$
$\Rightarrow x=\frac{3}{4\pi }\cos \left( \frac{20\pi t}{3}+\frac{\pi }{3}-\frac{\pi }{2} \right)\Rightarrow x=\frac{3}{4\pi }\cos \left( \frac{20\pi t}{3}-\frac{\pi }{6} \right)\left( cm \right)$. Chọn D
|
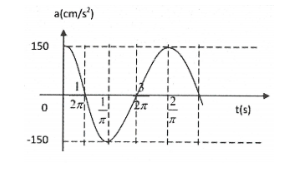
Bài tập 8: Hình bên là đồ thị bieru diễn sự phụ thuộc của gia tốc a theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là: B. $x=4\cos \left( 2\pi t+\frac{\pi }{4} \right)cm$ C. $x=8\cos \left( \pi t-\frac{\pi }{4} \right)cm$ D.$x=4\cos \left( 2\pi t-\frac{3\pi }{4} \right)cm$ |
Lời giải chi tiết
Ta có: ${{a}_{\max }}={{\omega }^{2}}A=16{{\pi }^{2}}\left( cm/{{s}^{2}} \right)$
Lại có: ${{t}_{\left( \frac{{{a}_{\max }}\sqrt{2}}{2}\to 0\to {{a}_{\max }} \right)}}={{t}_{\left( \frac{A\sqrt{2}}{2}\to 0\to A \right)}}=\frac{T}{8}+\frac{T}{4}=\frac{3T}{8}=\frac{3}{8}\Rightarrow T=1s$
Khi đó $\omega =\frac{2\pi }{T}=2\pi $
Tại thời điểm ban đầu $\left\{ \begin{array}{} a=\frac{-{{a}_{\max }}\sqrt{2}}{2} \\ {} a\uparrow \\ \end{array} \right.\Rightarrow {{\varphi }_{0a}}=\frac{-3\pi }{4}$
Do đó $a=16{{\pi }^{2}}\cos \left( 2\pi t-\frac{3\pi }{4} \right)\Rightarrow x=4\cos \left( 2\pi t-\frac{3\pi }{4}+\pi \right)=4\cos \left( 2\pi t+\frac{\pi }{4} \right)cm$. Chọn B
|
|
Lời giải chi tiết
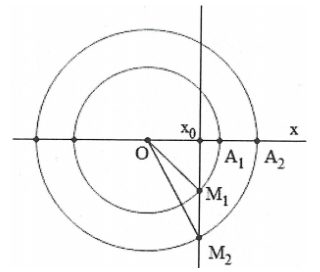
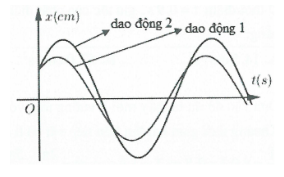
Ta có:${{v}_{2\max }}={{\omega }_{2}}A=4\pi \Rightarrow {{\omega }_{2}}=\frac{2\pi }{3}\Rightarrow {{T}_{2}}=\frac{2\pi }{{{\omega }_{2}}}=3\left( s \right)$
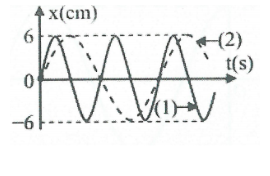
Dựa vào đồ thị ta thấy rằng ${{T}_{1}}=\frac{{{T}_{2}}}{2}=1,5\left( s \right)$
Phương trình dao động của 2 vật: ${{x}_{1}}=6\cos \left( \frac{2\pi t}{{{T}_{1}}}-\frac{\pi }{2} \right)\left( cm \right);{{x}_{2}}=6\cos \left( \frac{2\pi t}{{{T}_{2}}}-\frac{\pi }{2} \right)\left( cm \right)$
Không kể thời điểm t = 0 thì sau 3s hai vật gặp nhau 4 lần
Thời điểm 2 vật gặp nhau lần đầu tiên thỏa mãn $\frac{2\pi }{{{T}_{1}}}t-\frac{\pi }{2}=\frac{\pi }{2}-\frac{2\pi }{{{T}_{2}}}t\Rightarrow \left( \frac{1}{{{T}_{1}}}+\frac{1}{{{T}_{2}}} \right)t=\frac{1}{2}\Rightarrow t=0,5$
Do đó sau 3 + 0,5 = 3,5 (s) thì 2 vật đã gặp nhau 5 lần. Chọn D
|
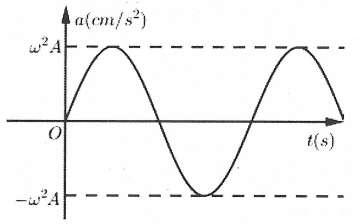
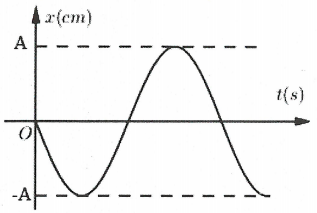
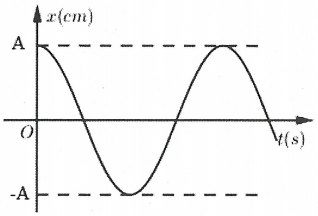
Bài tập 10: Đồ thị biểu diễn gia tốc a của một dao động điều hòa theo thời gian như sau: Đồ thị li độ x tương ứng là: A. |
|
C. |
Lời giải chi tiết
Ta có: $x=-{{\omega }^{2}}x$. Tại thời điểm ban đầu $a=0\Rightarrow x=0$ (loại đáp án C và D)
Tại thời điểm $t=\frac{T}{4}$ ta có $a={{\omega }^{2}}A\Rightarrow x=-A$ (loại đáp án A). Chọn B
|
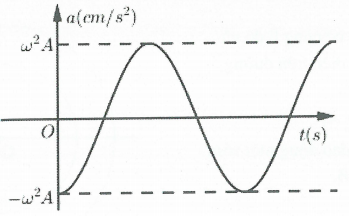
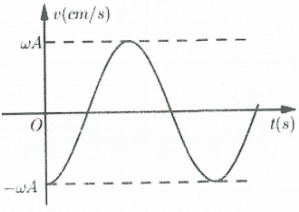
Bài tập 11: Đồ thị biểu diễn gia tốc a của một dao động điều hòa theo thời gian như sau: Đồ thị của vận tốc tương ứng là: A. |
|
C. |
Lời giải chi tiết
Tại thời điểm ban đầu ta có: $a=-{{\omega }^{2}}x=-{{\omega }^{2}}A\Rightarrow x=A\Rightarrow v=0$ (loại A và D) ( lúc này vật đang ở vị trí biên dương)
Ngay sau đó vật đi về vị tríc cân bằng và vận tốc của vật khi đi từ biên dương về VTCB nhỏ hơn 0 (oại đáp án B). Chọn C
|
|
Lời giải chi tiết

|
|
Lời giải chi tiết
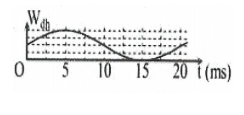
Thế năng đàn hồi $F=\frac{k\vartriangle {{\ell }^{2}}}{2}$
Đồ thị là dạng hình sin nên thế năng đàn hồi biến thiên tuần hoàn với tần số bằng 2 lần tần số dao động điều hòa của vật
Nhìn vào đồ thị hình sin của thế năng đàn hồi ta thấy khoảng thời gian từ điểm cao nhất đến điểm thấp nhất của đồ thị chênh lệch về thời gian là $15-5=10\left( ms \right)=\frac{T}{2}$
Chu kì dao động của thế năng là 20 ms nên tần số của thế năng là $\frac{1}{T}=50Hz$
Vậy tần số dao động của vật là 25Hz
Chú ý: Trong trường hợp con lắc lò xo treo thẳng đứng có $A>\Delta \ell $ thì đồ thị của thế năng đàn hồi vào thời gian không có dạng hình sin
|
|
Lời giải chi tiết
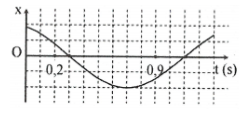
Dựa vào đồ thị ta thấy mỗi ô vuông ứng với thời gian là 0,1s
Khoảng thời gian 2 lần liên tiếp vật có li độ $x=0$ là( ứng với 8 ô)
$\frac{T}{2}=8.0,1=0,8\Rightarrow T=1,6s\Rightarrow \omega =\frac{2\pi }{T}=\frac{5\pi }{4}$
Tại thời điểm t = 0,3s ta có:$\left\{ \begin{array}{} x=0\,cm \\ {} v<0 \\ \end{array} \right.\Rightarrow {{\varphi }_{3}}=\frac{\pi }{2}$
Pha dao động tại thời điểm t = 0,2s là ${{\varphi }_{2}}={{\varphi }_{3}}-\frac{5\pi }{4}.0,1=\frac{3\pi }{8}$
Do đó $A\cos \frac{3\pi }{8}=2\Rightarrow A=5,226cm$
Mặt khác $\Delta t={{t}_{0,2\to 0,9}}=0,7s\Rightarrow \Delta \varphi =0,7.\frac{5\pi }{4}=\frac{7\pi }{8}$
Do đó ${{x}_{t=0,9}}=A\cos \left( \frac{3\pi }{8}+\frac{7\pi }{8} \right)=-3,696\Rightarrow a=-{{\omega }^{2}}x=57cm/{{s}^{2}}$. Chọn B
|
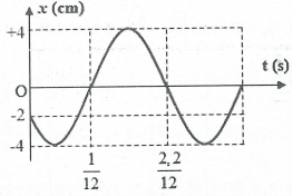
Bài tập 15: [Chuyên Quốc học Huế 2017]. Hình vẽ là đồ thị biểu diễn độ dời của dao động x theo thời gian t của 1 vật dao động điều hòa. Phương trình dao động của vật là: A. $x=4\cos \left( 10\pi t+\frac{2\pi }{3} \right)cm$ B. $x=4\cos \left( 20\pi t+\frac{2\pi }{3} \right)cm$ C. $x=4\cos \left( 10\pi t+\frac{5\pi }{6} \right)cm$ D.$x=4\cos \left( 20\pi t-\frac{\pi }{3} \right)cm$ |
|
Lời giải chi tiết
Ta có $A=4cm,\frac{T}{2}=\frac{2,2-1}{12}\Rightarrow T=\frac{1}{5}\left( s \right)\Rightarrow \omega =10\pi $
Tại thời điểm t = 0 ta có $\left\{ \begin{array}{} x=-2=-\frac{A}{2} \\ {} v<0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=\frac{2\pi }{3}$. Chọn A
|
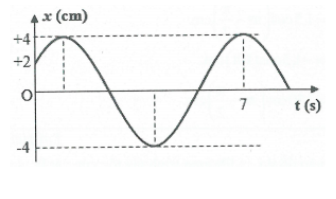
Bài tập 16: [Trích Đề thử Chuyên Đại học Vinh 216] Đồ thị dao động của một chất điểm dao động điều hòa như hình vẽ. Phương trình biểu diễn sự phụ thuộc của vận tốc của vật theo thời gian là B. $v=\frac{4\pi }{3}\cos \left( \frac{\pi t}{6}+\frac{5\pi }{6} \right)cm/s$ C. $v=4\pi \cos \left( \frac{\pi t}{3}+\frac{\pi }{3} \right)cm/s$ D. $v=4\pi \cos \left( \frac{\pi t}{6}+\frac{\pi }{3} \right)cm/s$ |
Lời giải chi tiết
Dựa vào đồ thị ta thấy: tại thời điểm $t=0\Rightarrow \left\{ \begin{array}{} x=2 \\ {} v>0 \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}=-\frac{\pi }{3}$
Lại có: ${{t}_{\left( 2\to 4 \right)}}+T=7\Rightarrow \frac{T}{6}+T=7\Rightarrow T=6s\Rightarrow \omega =\frac{\pi }{3}\left( rad/s \right)$
Do đó $x=4\cos \left( \frac{\pi t}{3}-\frac{\pi }{3} \right)cm\Rightarrow v=\frac{4\pi }{3}\cos \left( \frac{\pi t}{3}+\frac{\pi }{6} \right)cm/s$. Chọn A
|
Bài tập 17:[Trích Sở GD-ĐT Tây Ninh 2017] Cho hai dao dộng cùng phương có phương trình ${{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right)$và ${{x}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right)$(x tính bằng cm, t được tính bằng s). Đồ thị dao động tổng hợp $x={{x}_{1}}+{{x}_{2}}$ có dạng như hình vẽ. Cặp phương trình ${{x}_{1}},{{x}_{2}}$nào sau đây thỏa mãn điều kiện trên: B. ${{x}_{1}}=2\cos \left( \pi t-\frac{\pi }{2} \right)$ và ${{x}_{2}}=2\cos \left( \pi t+\frac{\pi }{2} \right)$ C. ${{x}_{1}}=6\cos \left( \pi t+\frac{\pi }{2} \right)$ và ${{x}_{2}}=2\cos \left( \pi t-\frac{\pi }{2} |
|
\right)$ D.${{x}_{1}}=4\cos \left( \pi t+\frac{\pi }{3} \right)$ và ${{x}_{2}}=4\cos \left( \pi t-\frac{\pi }{3} \right)$ |
Lời giải chi tiết
Dựa vào đồ thị ta có: $A=4cm,\frac{T}{2}=1s\Rightarrow T=2s\Rightarrow \omega =\pi \left( rad/s \right)$
Tại thời điểm $t=0\Rightarrow x=A\Rightarrow \varphi =0$. Do đó $x=4\cos \left( \pi t \right)$. Chọn D
|
|
Lời giải chi tiết
Dựa vào đồ thị $\Rightarrow $Phương trình gia tốc của vật là $a=150\cos \left( 10t \right)cm/{{s}^{2}}$
$\Rightarrow $Phương trình li độ của vật là$x=1,5\cos \left( 10t+\pi \right)=-1,5\cos \left( 10t \right)cm/s$. Chọn C
|
|
VẬT LÝ LỚP 12





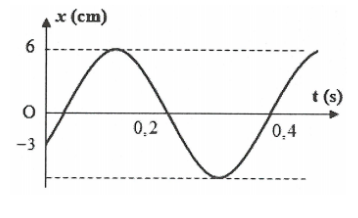 Bài tập 4: Một chất điểm dao động điều hòa dọc theo trục Ox, với O trùng với vị trí cân bằng của chất điểm. Đường biểu diễn sự phụ thuộc li độ chất điểm theo thời gian t cho ở hình vẽ. Phương trình vận tốc của chất điểm là:
Bài tập 4: Một chất điểm dao động điều hòa dọc theo trục Ox, với O trùng với vị trí cân bằng của chất điểm. Đường biểu diễn sự phụ thuộc li độ chất điểm theo thời gian t cho ở hình vẽ. Phương trình vận tốc của chất điểm là: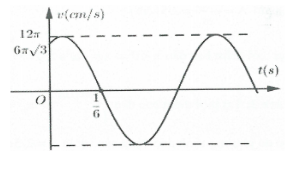 Bài tập 5: Một chất điểm dao động điều hòa dọc theo trục Ox. Đường biểu diễn sự phụ thuộc vận tốc chất điểm theo thời gian t cho ở hình vẽ. Phương trình dao động của chất điểm là:
Bài tập 5: Một chất điểm dao động điều hòa dọc theo trục Ox. Đường biểu diễn sự phụ thuộc vận tốc chất điểm theo thời gian t cho ở hình vẽ. Phương trình dao động của chất điểm là: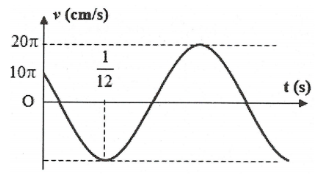 A. $x=2,5cos\left( 8\pi t+\frac{5\pi }{6} \right)cm$
A. $x=2,5cos\left( 8\pi t+\frac{5\pi }{6} \right)cm$ A.$x=\frac{3}{8\pi }\cos \left( \frac{40\pi }{3}t+\frac{\pi }{6} \right)\left( cm \right)$
A.$x=\frac{3}{8\pi }\cos \left( \frac{40\pi }{3}t+\frac{\pi }{6} \right)\left( cm \right)$ 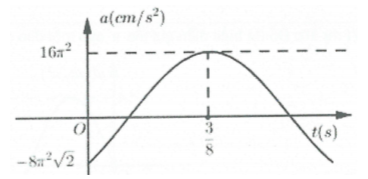 A. $x=4\cos \left( 2\pi t-\frac{\pi }{4} \right)cm$
A. $x=4\cos \left( 2\pi t-\frac{\pi }{4} \right)cm$ 
 B.
B. 
 D.
D. 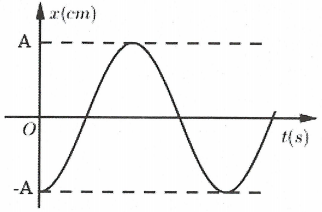
 B.
B. 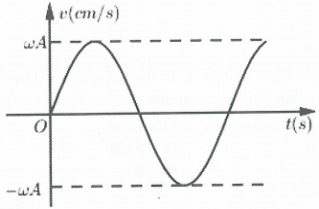
 D.
D. 



 A. $v=\frac{4\pi }{3}\cos \left( \frac{\pi t}{3}+\frac{\pi }{6} \right)cm/s$
A. $v=\frac{4\pi }{3}\cos \left( \frac{\pi t}{3}+\frac{\pi }{6} \right)cm/s$ 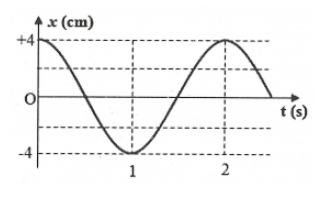 A. ${{x}_{1}}=2\sqrt{2}\cos \left( \pi t-\frac{\pi }{4} \right)$ và ${{x}_{2}}=2\sqrt{2}\cos \left( \pi t+\frac{\pi }{4} \right)$
A. ${{x}_{1}}=2\sqrt{2}\cos \left( \pi t-\frac{\pi }{4} \right)$ và ${{x}_{2}}=2\sqrt{2}\cos \left( \pi t+\frac{\pi }{4} \right)$