Bài tập độ lệch pha sóng cơ có đáp án chi tiết

BÀI TẬP ĐỘ LỆCH PHA SÓNG CƠ CÓ ĐÁP ÁN CHI TIẾT
|
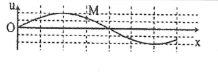
Bài tập 1: [Trích đề thi THPT QG năm 2017]. Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm ${{t}_{0}}$ một đoạn của sợi dây có dạng như hình bên. Hai phần tử tại M và O dao động lệch pha nhau. A. $\frac{\pi }{4}$ B. $\frac{\pi }{3}$ C. $\frac{3\pi }{4}$ D. $\frac{2\pi }{3}$ |
Lời giải chi tiết:
Nếu tính 1 ô là một đơn vị thì bước sóng là $\lambda =8$.
Độ dài OM là $OM=3.$
Độ lệch pha giữa 2 phần tử tại M và O là $\Delta \varphi =\frac{2\pi .OM}{\lambda }=\frac{3\pi }{4}$. Chọn C
|
Bài tập 2: Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20 Hz, có tốc độ truyền sóng nằm trong khoảng từ 0,7 m/s đến 1 m/s. Gọi A và B là 2 điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 10cm. Hai phần tử môi trường tại A và B luôn dao động ngược pha với nhau. Tốc độ truyền sóng là A. 90 cm/s B. 80 cm/s C. 85 cm/s D. 100 cm/s |
Lời giải chi tiết:
Hai phần tử môi trường tại A và B luôn dao động ngược pha với nhau nên
$AB=\left( k+0,5 \right)\lambda =0,1\Leftrightarrow \left( k+0,5 \right).\frac{v}{f}=0,1\Leftrightarrow v=\frac{2}{k+0,5}\left( k\in \mathbb{Z} \right).$
Cho $0,7<\frac{2}{k+0,5}<1\Rightarrow \left\{ \begin{array}{} k=2 \\ {} v=0,8\text{ }m/s=80\text{ }cm/s \\ \end{array} \right.$. Chọn B.
|
Bài tập 3: Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số f nằm trong khoảng 60 Hz đến 75 Hz, tốc độ truyền sóng là 100 cm/s. Gọi A và B là 2 điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 6,25 cm. Hai phần tử môi trường tại A và B luôn dao động ngược pha nhau. Tần số dao động của nguồn là A. f = 65 Hz. B. f = 75 Hz. C. f = 72 Hz. D. f = 68 Hz. |
Lời giải chi tiết:
Hai phần tử môi trường tại A và B luôn dao động ngược pha nhau nên
$AB=\left( k+0,5 \right)\lambda =\left( k+0,5 \right).\frac{100}{f}=6,25\Leftrightarrow f=16\left( k+0,5 \right)\left( k\in \mathbb{Z} \right).$
Cho $60<16\left( k+0,5 \right)<75\Leftrightarrow 3,25<k<4,1875\Rightarrow k=4.$ Khi đó f=72 Hz. Chọn C
|
Bài tập 4: Một sóng cơ học có tần số f = 40 Hz và bước sóng có giới hạn từ 18cm đến 30cm. Biết hai điểm M, N trên phương truyền sóng cách nhau khoảng 20 cm luôn luôn dao động cùng pha. Tìm vận tốc truyền sóng. A. v = 8 m/s. B. v = 6 m/s. C. v = 10 m/s. D. v = 12 m/s. |
Lời giải chi tiết:
Hai phần từ môi trường tại M, N luôn dao động cùng pha nhau nên
$MN=k\lambda =k\frac{v}{f}=k.\frac{v}{40}=20\Rightarrow v=\frac{80}{k}\left( k\in \mathbb{Z} \right).$
Cho $18<\frac{80}{k}<25\Leftrightarrow 4,44>k>3,2\Rightarrow k=4\Rightarrow \lambda =20$cm
$\Rightarrow v=\lambda f=800$cm/s$=$8 m/s. Chọn A
|
Bài tập 5: [Trích Chuyên ĐH Vinh 2017]. Một sóng ngang truyền trên sợi dây rất dài với tốc độ truyền sóng là 4m/s và tần số sóng có giá trị từ 41 Hz đến 69 Hz. Biết hai phần tử tại 2 điểm nêu trên dây cách nhau 25cm và luôn dao động ngược pha nhau. Tần số sóng trên đây là A. 64 Hz B. 48 Hz C. 56 Hz D. 52 Hz |
Lời giải chi tiết:
Ta có: $\Delta d=25cm=\left( k+0,5 \right)\lambda =\left( k+0,5 \right)\frac{v}{f}=8\left( 2k+1 \right)$.
Theo giả thuyết $41\le 8\left( 2k+1 \right)\le 69\Rightarrow \left\{ \begin{array}{} k=3 \\ {} f=56\text{ }Hz \\ \end{array} \right.$. Chọn C.
|
Bài tập 6: Một sợi dây đàn hồi rất dài có đầu A dao động với tần số f và theo phương vuông góc với dây. Tốc độ truyền sóng trên dây v = 2m/s. Xét một điểm M trên dây và cách A một đoạn 25cm luôn dao động ngược pha với điểm A. Biết tần số f dao động trong khoảng 18 Hz đến 22 Hz. Tính bước sóng $\lambda $. A. 0,1 m. B. 0,2m. C. 0,3m. D. 0,4m. |
Lời giải chi tiết:
M luôn ngược pha với A$\Rightarrow \frac{2\pi {{d}_{AM}}}{\lambda }=\pi +k2\pi \Leftrightarrow \frac{f}{v}.{{d}_{AM}}=\frac{1}{2}+k\Leftrightarrow f=\frac{\left( 0,5v+k \right)}{{{d}_{AM}}}$
Theo bài $18<f<22\Rightarrow 18<\frac{\left( 0,5v+k \right)}{{{d}_{AM}}}<22\Rightarrow 18<4\left( k+1 \right)<22\Leftrightarrow 3,5<k<4,5$
$\Rightarrow k=4$. Tần số dao động của vật $f=22$ Hz. Bước sóng $\lambda =\frac{v}{f}=\frac{2}{20}=0,1$ m/s. Chọn A.
|
Bài tập 7: Mũi nhọn S chạm vào mặt nước dao động điều hòa với tần số 20 Hz. Thấy rằng 2 điểm A và B cùng nằm trên phương truyền sóng cách nhau 32,5 cm luôn dao động vuông pha. Tính vận tốc truyền sóng biết vận tốc dao động trong khoảng 1,8 m/s đến 2,4 m/s A. 1,85 m/s B. 2 m/s C. 2,2 m/s D. 2,3 m/s |
Lời giải chi tiết:
A và B là 2 điểm luôn vuông pha nhau:
$\frac{2\pi {{d}_{AB}}}{\lambda }=\frac{\pi }{2}+k2\pi \Leftrightarrow {{d}_{AB}}=\left( k+\frac{1}{4} \right)\frac{v}{f}\Leftrightarrow v=\frac{{{d}_{AB}}f}{k+0,25}$
Vận tốc truyền sóng luôn dao động trong khoảng 0,85 m/s đến 1,2 m/s
$\Rightarrow 0,85<v<1,2\Leftrightarrow 180<\frac{df}{k+0,25}<240\Leftrightarrow 180<\frac{32,5.20}{k+0,25}<240\Leftrightarrow 2,45<k<3,36$
k nguyên $\Rightarrow k=3$$\Rightarrow $ Vận tốc truyền sóng $v=200$cm/s $=$2 m/s. Chọn B.
|
Bài tập 8: Trong môi trường đàn hồi có một sóng cơ có tần số f = 30 Hz. Hai điểm M và N trên cùng phương truyền sóng dao động ngược pha nhau, giữa chúng có 3 điểm khác cũng dao động ngược pha với M. Khoảng cách MN là 8,4 cm. Vận tốc truyền sóng là A. v = 100 cm/s. B. v = 80 cm/s. C. v = 72 cm/s. D. v= 120 cm/s. |
Lời giải chi tiết:
Khoảng cách ngắn nhất giữa 2 điểm dao động ngược pha nhau là $\frac{\lambda }{2}$.
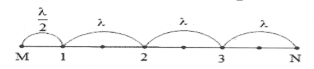
Khoảng cách giữa 2 điểm M,N là $d=\frac{\lambda }{2}+3\lambda =\frac{7}{2}\lambda =\frac{7}{2}.\frac{v}{f}=8,4\Rightarrow v=72cm/s$. Chọn C.
|
Bài tập 9: Một sóng cơ học có tần số f = 50 Hz, tốc độ truyền sóng là v = 150 cm/s. Hai điểm M và N trên phương truyền sóng dao động ngược pha nhau, giữa chúng có 30 điểm khác cũng dao động cùng pha với M. Khoảng cách MN là A. d = 157,5 cm. B. d = 91,5 cm. C. d = 97,5 cm. D. d = 94,5 cm. |
Lời giải chi tiết:
Ta có: $\lambda =\frac{v}{f}=3\text{ }cm.$
Giữa MN có 30 điểm cùng pha với M nên $MN=30\lambda +\frac{\lambda }{2}=31,5\lambda =94,5cm$.Chọn D.
|
Bài tập 10: Một sóng cơ học được phát ra từ nguồn O với tần số f = 40 Hz, tốc độ truyền sóng là v = 120 cm/s. Gọi A và B là 2 điểm nằm trên Ox, ở cùng một phía với O và cách O một khoảng lần lượt là 30 cm và 45 cm. Trên đoạn AB số điểm luôn dao động vuông pha với nguồn là A. 6. B. 7. C. 8. D. 9. |
Lời giải chi tiết:
Điểm M vuông pha với nguồn thỏa mãn
![]()
$\frac{2\pi OM}{\lambda }=k2\pi +\frac{\pi }{2}\Leftrightarrow OM=k\lambda +\frac{\lambda }{4}$
Do M nằm trên đoạn AB nên $30\le \left( k+\frac{1}{4} \right).\frac{v}{f}\le 45$
$\Leftrightarrow 30\le \left( k+0,5 \right).2\le 45\Leftrightarrow 14,75\le k\le 22,25\left( k\in \mathbb{Z} \right).$
Khi đó $k=15,16...22\Rightarrow $có 8 điểm dao động vuông pha với nguồn. Chọn C.
|
Bài tập 11: Một nguồn O phát ra sóng cơ dao động theo phương trình $u=2\cos \left( 20\pi t+\frac{\pi }{3} \right)$cm. Sóng truyền theo đường thẳng Ox với tốc độ không đổi 1 m/s. Xét trên một phương truyền sóng từ O đến điểm M rồi N có OM = 10 cm, ON = 55 cm. Trong đoạn MN có bao nhiêu điểm vuông pha với nguồn. A. 10 B. 8 C. 9 D. 5 |
Lời giải chi tiết:
Bước sóng$\lambda =vT=10\text{ }cm$
Một điểm trên MN dao động vuông pha với nguồn khi $ {} \frac{2\pi d}{\lambda }=\frac{\pi }{2}+k\pi \Leftrightarrow d=\frac{\lambda }{4}+\frac{k\lambda }{2}$
Ta luôn có $OM\le d\le ON\Leftrightarrow 10\le \frac{\lambda }{4}+\frac{k\lambda }{2}\le 55\Leftrightarrow 1,5\le k\le 10,5$
$\Rightarrow $ Trên đoạn MN có 9 điểm dao động vuông pha với nguồn. Chọn C.
|
Bài tập 12: [Trích đề thi đại học năm 2013]. Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng $\lambda $. Hai điểm M và N thuộc mặt nước, nằm trên 2 phương truyền sóng mà các phần tử nước đang dao động. Biết $OM=8\lambda $,$ON=12\lambda $ và OM vuông góc với ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là A. 5 B. 6 C. 7 D. 4 |
Lời giải chi tiết:
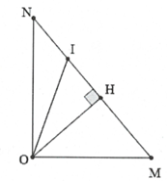
Điểm I trên MN dao động ngược pha với nguồn O thỏa mãn:
$OI=\left( k+0,5 \right)\lambda $.
Dựng $OH\bot MN\Rightarrow OH=\frac{OM.ON}{\sqrt{O{{M}^{2}}+O{{N}^{2}}}}=\frac{24\sqrt{13}}{13}$.
Số điểm ngược pha với O trên HN là:
$OH\le \left( k+0,5 \right)\lambda \le ON\Leftrightarrow 6,15\le k\le 11,5$
Suy ra có 5 giá trị của k
Số điểm ngược pha với O trên HM là:
$OH\le \left( k+0,5 \right)\lambda \le OM\Leftrightarrow 6,15\le k\le 7,5\Rightarrow k=7$
Vậy có tổng cộng 6 điểm dao động ngược pha với O trên MN. Chọn B.
|
Bài tập 13: Một nguồn điểm phát sóng dao động điều hòa theo phương thẳng đứng với tần số f = 20 Hz tạo ra sóng tròn đồng tâm tại O truyền trên mặt chất lỏng với tốc độ 40 cm/s. Hai điểm M và N thuộc chất lỏng mà phần tử tại N dao động cùng pha với phần tử chất lỏng tại O còn phần tử M dao động ngược pha với phần tử chất lỏng tại O. Không kể phần tử chất lỏng tại O, số phần tử chất lỏng dao động cùng pha với phần tử chất lỏng tại O trên đoạn MO là 8, trên đoạn NO là 5 và trên đoạn MN là 8. Khoảng cách giữa 2 điểm MN có giá trị gần nhất với giá trị nào sau đây? A. 26 cm. B. 18 cm. C. 14 cm. D. 22cm |
Lời giải chi tiết:
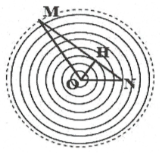
Bước sóng $\lambda =\frac{v}{f}=\frac{40}{20}=2$cm
Các đường tròn biểu diễn các điểm cùng pha với nguồn, N nằm trên đỉnh sóng thứ 5. M ngược pha nằm tại điểm gần đỉnh sóng thứ 8:
$\left\{ \begin{array}{} ON=5\lambda =10cm \\ {} OM=8,5\lambda =17cm \\ \end{array} \right.$
Từ hình vẽ thấy rằng, để trên đoạn MN có 8 điểm cùng pha với nguồn thì MN phải tiếp tuyến với đỉnh sóng thứ 3$\left( OH=3\lambda =6\text{ }cm \right).$
Ta có: $MN=MH+HN=\sqrt{M{{O}^{2}}-O{{H}^{2}}}+\sqrt{O{{N}^{2}}-O{{H}^{2}}}$
$\Rightarrow MN=\sqrt{{{17}^{2}}-{{6}^{2}}}+\sqrt{{{10}^{2}}-{{6}^{2}}}\approx 23,9cm$. Chọn D
|
Bài tập 14: Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng $\lambda $. Ba điểm A, B, C trên hai phương truyền sóng sao cho OA vuông góc với OC và B là một điểm thuộc tia OA sao cho $OB>OA$. Biết $OA=7\lambda $. Tại thời điểm người ta quan sát thấy giữa A và B có 5 đỉnh sóng (kể cả A và B) và lúc này $\widehat{ACB}$đạt giá trị lớn nhất. Số điểm dao động ngược pha với nguồn trên đoạn AC là A. 7 B. 5 C. 6 D. 4 |
Lời giải chi tiết:
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng$\Rightarrow AB=4\lambda $. Chuẩn hóa $\lambda =1$
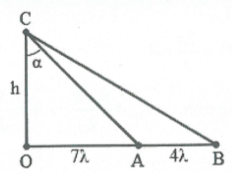
Ta có$\left\{ \begin{array}{} \tan \alpha =\frac{7\lambda }{h} \\ {} \tan \beta =\frac{11\lambda }{h} \\ \end{array} \right.\Rightarrow \tan \left( \beta -\alpha \right)=\tan \widehat{ACB}=\frac{\frac{4\lambda }{h}}{1+\frac{77{{\lambda }^{2}}}{{{h}^{2}}}}=\frac{4\lambda }{h+\frac{77{{\lambda }^{2}}}{h}}$
Áp dụng công thức bất đẳng thức cosi, dễ dàng thấy được rằng $\widehat{ACB}$ lớn nhất khi $h=\sqrt{77}$.
Gọi M là điểm trên AC, để M ngược pha với nguồn thì
$\frac{2\pi {{d}_{M}}}{\lambda }=\left( 2k+1 \right)\pi \Rightarrow {{d}_{M}}=\left( 2k+1 \right)0,5$
Với khoảng giá trị của ${{d}_{M}}$, tính về phía C từ đường vuông góc của O lên AC: $5,46\le {{d}_{M}}\le 8,7$; kết hợp với chức năng Mode$\Rightarrow $ta tìm được 4 vị trí
Tương tự như vậy, xét đoạn về phía A: $5,46\le {{d}_{M}}\le 7$ta tìm được 2 vị trí
$\Rightarrow $ Trên AC có 6 vị trí dao động ngược pha với nguồn. Chọn C.
|
Bài tập 15: Một sóng ngang có bước sóng $\lambda $ lan truyền trên một sợi dây dài qua M rồi đến N cách nhau 5,25$\lambda $. Tại một thời điểm nào đó M có li độ âm và đang đi lên thì N đang có li độ A. Âm, đi xuống. B. Âm, đi lên. C. Dương, đi xuống. D. Dương, đi lên. |
Lời giải chi tiết:
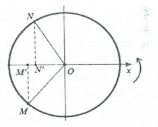
Điểm M nhanh pha hơn N góc $\frac{21}{2}\pi =10\pi +\frac{\pi }{2}$. Do đó khi M có li độ âm và đang đi lên thì điểm N có li độ âm và đi xuống.
Chọn A.
|
Bài tập 16: Một sóng ngang có bước sóng $\lambda $ lan truyền trên một sợi dây dài qua M rồi đến N cách nhau $d=1,25\lambda $. Tại cùng một thời điểm nào đó M có li độ -6 cm và N có li độ -8cm. Tính giá trị của biên độ sóng. A. 12 cm B. 2 cm C. 14 cm D. 10 cm |
Lời giải chi tiết:
Độ lệch pha $\Delta \varphi =\frac{2\pi .1,25\lambda }{\lambda }=\frac{5}{2}\pi $ do đó 2 phần tử M và N dao động vuông pha nhau.
Khi đó ta có: $A=\sqrt{{{u}^{2}}_{M}+{{u}^{2}}_{N}}=10cm$.Chọn D.
|
Bài tập 17: Hai điểm M và N cùng nằm trên phương truyền sóng cách nhau $\frac{\lambda }{3}$, sóng có biên độ A, chu kỳ T. Sóng truyền từ N đến M. Gỉa sử tại điểm ${{t}_{1}}$có ${{u}_{M}}=4\text{ }cm$và ${{u}_{N}}=-4\text{ }cm$. Biên độ sóng là? A. 4 cm. B. $\frac{8}{\sqrt{3}}\text{ cm}\text{.}$ C. $\frac{4}{\sqrt{3}}\text{ cm}\text{.}$ D. $4\sqrt{2}\text{ cm}\text{.}$ |
Lời giải chi tiết:
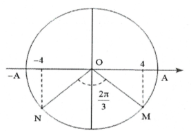
Ta có ${{d}_{MN}}=\frac{\lambda }{3}$, độ lệch pha giữa 2 điểm M và N là
$\Delta \varphi =\frac{2\pi .{{d}_{MN}}}{\lambda }=\frac{2\pi }{3}rad$
Dựa vào đường tròn$\Rightarrow {{u}_{M}}=\frac{A\sqrt{3}}{2}\Rightarrow A=\frac{8}{\sqrt{3}}cm$. Chọn B.
|
Bài tập 18: [Trích đề thi đại học 2012]. Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li độ dao động của phần tử tại M là 3 cm thì li độ dao động của phần tử tại N là $-3$cm. Biên độ sóng bằng A. 6 cm. B. $2\sqrt{3}\text{ cm}\text{.}$ C. 3 cm. D. $3\sqrt{2}\text{ cm}\text{.}$ |
Lời giải chi tiết:
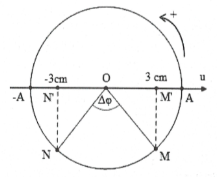
Độ lệch pha giữa 2 điểm M và N là $\Delta \varphi =\frac{2\pi d}{\lambda }=\frac{2}{3}\pi $.
Sóng truyền từ M đến N và tại một thời điểm nào đó phần tử tại M là 3 cm thì li độ dao động của phần tử tại N là -3cm nên 2 điểm M, N được biểu diễn trên đường tròn như hình vẽ.
Ta có: $\widehat{NO{N}'}=\frac{180{}^\circ -120{}^\circ }{2}=30{}^\circ $.
Suy ra $ON\cos 30{}^\circ =O{N}'\Rightarrow ON=2\sqrt{3}=A$. Chọn B.
|
Bài tập 19: Có 2 điểm A, B trên phương truyền sóng và cách nhau một phần tư bước sóng. Tại thời điểm t nào đó, A và B đang cao hơn vị trí cân bằng lần lượt là 2 cm và 3 cm. Biết A đang đi xuống còn B đang đi lên. Coi biên độ sóng không đổi. Xác định biên độ sóng a và chiều truyền sóng A. $a=5\text{ }cm,$truyền từ A sang B. B. $a=5\text{ }cm,$truyền từ B sang A. C. $a=\sqrt{13}\text{ }cm,$truyền từ A sang B. D. $a=\sqrt{13}\text{ }cm,$truyền từ B sang A. |
Lời giải chi tiết:

Do 2 điểm cách nhau $\frac{\lambda }{4}$ nên vuông pha với nhau. Do đó
$a=\sqrt{{{u}^{2}}_{A}+{{u}^{2}}_{B}}=\sqrt{13}$(cm). Vì A, B cao hơn vị trí cân bằng (li độ dương), A đi xuống, B đi lên nên A nhanh pha hơn B do đó sóng truyền A đến B (hình vẽ). Chọn C.
|
Bài tập 20: Một sóng ngang có bước sóng $\lambda $ lan truyền trên một sợi dây dài qua M rồi đến N cách nhau $\text{ }\!\!\lambda\!\!\text{ /6}\text{.}$ Tại một thời điểm nào đó M có li độ$2\sqrt{3}\text{ }cm$ và N có li độ$-2\text{ }cm$. Tính giá trị của biên độ sóng. A. 6cm B. 7,4cm C. 5,53cm D. 6,4cm |
Lời giải chi tiết:
.
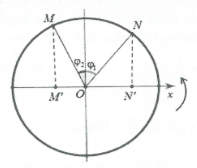
Độ lệch pha giữa M và N là: $\Delta \varphi =\frac{2\pi \lambda }{\lambda .6}=\frac{\pi }{3}.$
Khi đó ${{\varphi }_{1}}+{{\varphi }_{2}}=\frac{\pi }{3}.$
Mặt khác $A\sin {{\varphi }_{1}}=2\sqrt{3};A\sin {{\varphi }_{2}}=2$
Do đó:$\left\{ \begin{array}{} {{\varphi
VẬT LÝ LỚP 12