Bài tập công suất và hệ số công suất có đáp án chi tiết

BÀI TẬP CÔNG SUẤT VÀ HỆ SỐ CÔNG SUẤT CÓ ĐÁP ÁN CHI TIẾT

Lời giải chi tiết

Hệ số công suất $\cos \varphi =\frac{R}{Z}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}$.Chọn C.

Lời giải chi tiết

Hệ số công suất của đoạn mạch $\cos \varphi =\frac{{{U}_{R}}}{U}=\frac{100}{200}=0,5$. Chọn D.

Lời giải chi tiết

Ta có: $P=UI.\cos \varphi =U.\frac{U}{Z}.\frac{R+r}{Z}=\left( R+r \right).\frac{{{U}^{2}}}{{{Z}^{2}}}=\left( R+r \right){{I}^{2}}.$Chọn B.

Lời giải chi tiết

Ta có công suất tiêu thụ trên mạch chỉ có điện trở R là $P=\frac{{{U}^{2}}}{R}=400W.$Chọn D.

Lời giải chi tiết

Theo giả thiết bài toán ta có: $R={{Z}_{L}}={{Z}_{C}}\Rightarrow {{U}_{R}}={{U}_{L}}={{U}_{C}}.$

Trong đó: ${{Z}_{L}}=100\Omega $, mặt khác $U=\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}={{U}_{R}}\Rightarrow {{U}_{R}}=100V.$

Do đó $I=1A\Rightarrow P=UI\cos \varphi =100.1.\cos 0=100W.$ Chọn A.

Lời giải chi tiết

Ta có: $P=R{{I}^{2}}=R\frac{I_{0}^{2}}{2}=10W.$Chọn A.

Lời giải chi tiết

Ta có: $\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=-\frac{\pi }{2}+\frac{\pi }{4}=-\frac{\pi }{4}.$

Do đó $P=UI\cos \varphi =220.2.\cos \left( -\frac{\pi }{4} \right)=220\sqrt{2}W.$Chọn B.

Lời giải chi tiết

Ta có độ lệch pha ${{\varphi }_{u/i}}=-\frac{\pi }{6}\Rightarrow $ hệ số công suất của đoạn mạch là

$\cos \varphi =\cos \left( -\frac{\pi }{6} \right)=\frac{\sqrt{3}}{2}=0,87.$Chọn B.

Lời giải chi tiết

Ta có: $\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\frac{\pi }{6}-\frac{\pi }{3}=-\frac{\pi }{6}.$

Do đó $P=UI\cos \varphi =100\sqrt{2}.\sqrt{2}.\cos \left( -\frac{\pi }{6} \right)=100\sqrt{3}W.$Chọn A.

Lời giải chi tiết

Ta có công suất toàn phần: $P=UI\cos \varphi =220.0,5.0,8=88W.$

Hiệu suất của động cơ là: $H=\frac{{{P}_{h/i}}}{{{P}_{tp}}}=\frac{88-11}{88}=87,5%.$ Chọn D.

Lời giải chi tiết

Ta có: $P=R{{I}^{2}}=R.\frac{{{U}^{2}}}{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\Rightarrow {{({{Z}_{L}}-{{Z}_{C}})}^{2}}=\frac{R{{U}^{2}}}{P}-{{R}^{2}}=0$

Do đó ${{Z}_{L}}={{Z}_{C}}\Leftrightarrow \omega =\frac{1}{\sqrt{LC}}=120\pi $rad/s. Chọn D.

Lời giải chi tiết

Ta có: điện áp tức thời giữa hai bản tụ và điện áp tức thời giữa hai đầu mạch lệch pha một góc $\pi /6$ suy ra ${{\varphi }_{u/i}}=\frac{\pi }{6}-\frac{\pi }{2}=-\frac{\pi }{3}.$

Khi đó công suất tiêu thụ của mạch là: $P=\frac{{{U}^{2}}}{R}{{\cos }^{2}}\varphi =50W.$Chọn A.

Lời giải chi tiết

Ta có: ${{U}^{2}}=U_{{{C}_{1}}}^{2}+U_{{{R}_{1}}}^{2}=U_{{{C}_{2}}}^{2}+U_{{{R}_{2}}}^{2}=\frac{1}{4}U_{{{C}_{1}}}^{2}+4U_{{{R}_{1}}}^{2}\Leftrightarrow \frac{3}{4}U_{{{C}_{1}}}^{2}=3U_{{{R}_{1}}}^{2}.$

$\Rightarrow \frac{{{U}_{{{R}_{1}}}}}{{{U}_{{{C}_{1}}}}}=\frac{1}{2}.$ Do đó $\cos {{\varphi }_{1}}=\frac{{{U}_{{{R}_{1}}}}}{\sqrt{U_{{{R}_{1}}}^{2}+U_{{{C}_{1}}}^{2}}}=\frac{1}{\sqrt{{{1}^{2}}+{{2}^{2}}}}=\frac{1}{\sqrt{5}}.$

Mặt khác $\frac{{{U}_{{{R}_{2}}}}}{{{U}_{{{C}_{2}}}}}=\frac{2{{U}_{{{R}_{1}}}}}{\frac{1}{2}{{U}_{{{C}_{1}}}}}=2\Rightarrow \cos {{\varphi }_{2}}=\frac{{{U}_{{{R}_{2}}}}}{\sqrt{U_{{{R}_{2}}}^{2}+U_{{{C}_{2}}}^{2}}}=\frac{2}{\sqrt{{{2}^{2}}+{{1}^{2}}}}=\frac{2}{\sqrt{5}}.$Chọn C.

Lời giải chi tiết

Tại thời điểm t ta có: $u=400V\Rightarrow {{\varphi }_{u}}=0\Rightarrow {{\varphi }_{i}}=-\alpha $ (với $\alpha ={{\varphi }_{u/i}}$ ).

Sau $t+\frac{1}{400}s\Rightarrow {{\varphi }_{i}}=-\alpha +\frac{1}{400}.100\pi =\frac{\pi }{2}\Rightarrow \alpha =-\frac{\pi }{4}.$

Do đó công suất của mạch X là: ${{P}_{x}}=P-{{P}_{R}}=UI\cos \varphi -R{{I}^{2}}=200\sqrt{2}.2.\cos \left( -\frac{\pi }{4} \right)-{{50.2}^{2}}=200W.$

Chọn C.

Lời giải chi tiết

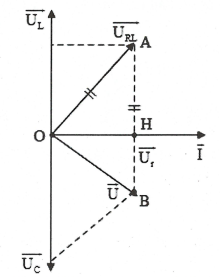
Vẽ giãn đồ vecto như hình vẽ bên. Ta có: ${{U}_{C}}={{U}_{RL}}$nên tam giác OAB cân tại A. Theo giả thiết ta có: $\widehat{HOB}=\frac{\pi }{12}={{15}^{0}}$ (Chú ý: Rõ ràng B nằm dưới trục OI vì $AB=OA>{{U}_{L}}$). Suy ra $\widehat{HOB}={{80}^{0}}-{{15}^{0}}={{75}^{0}}=\widehat{AOB}$. Do đó:    $\widehat{AOH}={{75}^{0}}-{{15}^{0}}={{60}^{0}}$ $\Rightarrow \cos {{\varphi }_{RL}}=\cos {{60}^{0}}=0,5.$Chọn C.

Lời giải chi tiết

Ta có: $P=UI\cos \varphi \Rightarrow I=\frac{P}{U\cos \varphi }=1A$.

Tổng trở của mạch là: $Z=\frac{U}{I}=\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=100\Omega .$.

$\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=\sqrt{3}\Rightarrow {{Z}_{L}}-{{Z}_{C}}=R\sqrt{3}\Rightarrow \left\{ \begin{array}{*{35}{l}}R=50\Omega   \\{{Z}_{L}}-{{Z}_{C}}=50\sqrt{3}\Omega   \\\end{array} \right.$

Khi mắc thêm điện trở ${{R}_{0}}$ thì $I'=I=1A\Rightarrow Z'=\frac{U'}{I'}=100\sqrt{3}.$

$\Rightarrow \sqrt{{{(R+{{R}_{0}})}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=100\sqrt{3}\Rightarrow {{R}_{0}}=100\Omega .$ Chọn C.

Lời giải chi tiết

Ta có: $\tan {{\varphi }_{AM}}=\frac{-{{Z}_{C}}}{R}=-1\Rightarrow {{\varphi }_{AM}}=-\frac{\pi }{4}={{\varphi }_{uAM}}-{{\varphi }_{i}}\Rightarrow {{\varphi }_{i}}=-\frac{7\pi }{12}+\frac{\pi }{4}=-\frac{\pi }{3}.$

Ta đã được học cách tổng hợp hai dao động bằng CASIO.

Ta có: ${{u}_{AB}}={{u}_{AM}}+{{u}_{MB}}=50\sqrt{2}\angle \frac{-7\pi }{12}+150\angle 0=148,36\angle -0,4784.$

Do đó ${{\varphi }_{u/i}}=-0,4784+\frac{\pi }{3}=0,569\Rightarrow \cos \varphi =0,84.$Chọn B.

Bài tập 18: [Trích đề thi thử Chuyên Đại học Vinh 2017] Đặt điện áp $u={{U}_{0}}\cos (\omega t)$(${{U}_{0}}$ và $\omega $ không đổi) vào hai đầu đoạn mạch AB như hình vẽ. Điện áp hai đầu đoạn mạch AB sớm pha $\pi /6$ so với cường độ dòng điện trong đoạn mạch, điện áp hai đầu đoạn mạch AM lệch pha $\pi /3$ so với cường độ dòng điện trong đoạn mạch. Tổng trở đoạn mạch AB và AM lần lượt là $200\Omega $ và $100\sqrt{3}\Omega $. Hệ số công suất của đoạn mạch X là: 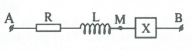A. $\sqrt{3}/2.$ B. 1/2 C. $\sqrt{2}/2.$ D. 0.

Lời giải chi tiết

Ta có: $\left\{ \begin{array}{*{35}{l}}\cos \frac{\pi }{6}=\frac{{{R}_{AB}}}{200}  \\\cos \frac{\pi }{3}=\frac{{{R}_{AM}}}{100\sqrt{3}}  \\\end{array} \right.\Rightarrow \left\{ \begin{array}{*{35}{l}}{{R}_{AB}}=100\sqrt{3}  \\{{R}_{AM}}=50\sqrt{3}  \\\end{array} \right.\Rightarrow {{R}_{x}}=50\sqrt{3}.$

Ta có: ${{u}_{AM}}$ sớm pha hơn ${{u}_{AB}}$ góc $\pi /6$.

Mặt khác $\overline{{{Z}_{AB}}}=\overline{{{Z}_{AM}}}+\overline{{{Z}_{X}}}\Rightarrow \overline{{{Z}_{X}}}=\overline{{{Z}_{AB}}}-\overline{{{Z}_{AM}}}.$

Suy ra $Z_{x}^{2}=\sqrt{Z_{AB}^{2}+Z_{AM}^{2}-2{{Z}_{AB}}.{{Z}_{AM}}\cos \frac{\pi }{6}}=100\Omega \Rightarrow \cos {{\varphi }_{x}}=\frac{{{R}_{X}}}{{{Z}_{X}}}=\frac{\sqrt{3}}{2}.$ Chọn A.

Lời giải chi tiết

Theo giả thiết bài toán ta có hệ:

$\left\{ \begin{array}{*{35}{l}}{{100}^{2}}={{(30+{{U}_{r}})}^{2}}+{{({{U}_{L}}-100)}^{2}}  \\{{30}^{2}}=U_{r}^{2}+U_{L}^{2}  \\\end{array} \right.\Leftrightarrow \left\{ \begin{array}{*{35}{l}}90+3{{U}_{r}}-10{{U}_{L}}=0  \\{{30}^{2}}=U_{r}^{2}+{{(9+0,3{{U}_{r}})}^{2}}  \\\end{array} \right.$.

Giải phương trình hoặc dùng SHIFT-CALC ta được: ${{U}_{r}}=25V\Rightarrow P={{U}_{R+r}}I=110W.$Chọn B,

Lời giải chi tiết

Công suất tiêu thụ trên mạch lúc đầu $\left\{ \begin{array}{*{35}{l}}{{P}_{1}}=\frac{R{{U}^{2}}}{{{R}^{2}}+Z_{C}^{2}}  \\\cos {{\varphi }_{1}}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}=0,5  \\\end{array} \right.$

Chuẩn hóa $R=1\Rightarrow {{Z}_{C}}=\sqrt{3}\Rightarrow {{P}_{1}}=\frac{{{U}^{2}}}{4}.$

Khi ${\omega }'=\sqrt{3}\omega \Rightarrow Z(C)=\frac{{{Z}_{C}}}{\sqrt{3}}=1\Rightarrow {{P}_{2}}=\frac{{{U}^{2}}R}{{{R}^{2}}+{Z}'_{C}^{2}}=\frac{{{U}^{2}}}{2}=2{{P}_{1}}.$ Chọn A.