Bài tập Biện luận số nghiệm của phương trình bằng phương pháp suy đồ thị

Bài tập Biện luận số nghiệm của phương trình bằng phương pháp suy đồ thị
Cách giải bài toán biện luận số nghiệm bằng phương pháp suy đồ thị
1. Các phép tịnh tiến đồ thị hàm số
Trong mặt phẳng tọa độ $Oxy$, cho đồ thị $\left( C \right)$ của hàm số $y=f\left( x \right)$, $p$ và $q$ là hai số dương tùy ý. Khi đó:
- Tịnh tiến $\left( C \right)$ lên trên $q$ đơn vị thì ta được đồ thị của hàm số $y=f\left( x \right)+q$.
- Tịnh tiến $\left( C \right)$ xuống dưới $q$ đơn vị thì ta được đồ thị của hàm số $y=f\left( x \right)-q$.
- Tịnh tiến $\left( C \right)$ sang trái $p$ đơn vị thì ta được đồ thị của hàm số $y=f\left( x+p \right)$.
- Tịnh tiến $\left( C \right)$ sang phải $p$ đơn vị thì ta được đồ thị của hàm số $y=f\left( x-p \right)$.
2. Một số phép suy đồ thị
þ Mẫu 1: Cho đồ thị hàm số $y=f\left( x \right)$$\left( C \right)$ thì đồ thị hàm số $y=\left| f\left( x \right) \right|$ gồm 2 phần.
- Phần 1: Là phần đồ thị hàm số $\left( C \right)$ nằm phía trên trục hoành.
- Phần 2: Lấy đối xứng phần của $\left( C \right)$ nằm dưới $Ox$ qua $Ox$.
þ Mẫu 2: Cho đồ thị hàm số $y=f\left( x \right)$$\left( C \right)$ suy ra đồ thị hàm số $y=f\left( \left| x \right| \right)$ gồm hai phần
- Phần 1: Là phần của $\left( C \right)$ nằm bên phải trục tung.
- Phần 2: Lấy đối xứng phần 1 qua trục tung (vì hàm số $y=f\left( \left| x \right| \right)$ là hàm chẵn nên nhận trục tung là trục đối xứng).
þ Mẫu 3: Cho đồ thị hàm số $y=u\left( x \right).v\left( x \right)\left( C \right)$ thì đồ thị hàm số $y=\left| u\left( x \right) \right|.v\left( x \right)$ gồm hai phần.
- Phần 1: Là phần của $\left( C \right)$ ứng với miền $u\left( x \right)\ge 0$.
- Phần 2: Lấy đối xứng phần của $\left( C \right)$ ứng với miền $u\left( x \right)<0$ qua trục $Ox$.
Bài tập trắc nghiệm biện luận số nghiệm của phương trình có đáp án
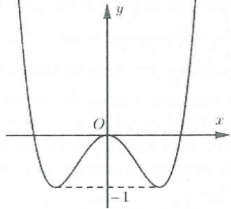
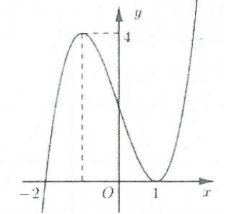
| Bài tập 1: Cho hàm số $y={{x}^{4}}-2{{x}^{2}}$ có đồ thị như hình vẽ.
Tìm tất cả các giá trị của tham số $m$ để phương trình $\left| {{x}^{4}}-2{{x}^{2}} \right|=m$ có 4 nghiệm phân biệt A. $m=1$ B. $m=0$ C. $m>1$ D. $0<m<1$ |
Lời giải chi tiết
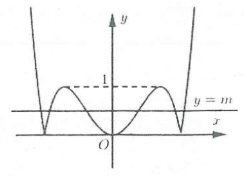
Gọi $y={{x}^{4}}-2{{x}^{2}}\left( C \right)$. Đồ thị hàm số $y=\left| {{x}^{4}}-2{{x}^{2}} \right|$ gồm 2 phần:
Phần 1: Là phần đồ thị hàm số $\left( C \right)$ nằm phía bên trục hoành.
Phần 2: Lấy đối xứng phần của $\left( C \right)$ nằm dưới $Ox$ qua $Ox$.
Dựa vào đồ thị hàm số $y=\left| {{x}^{4}}-2{{x}^{2}} \right|$ (hình vẽ) và đường thẳng $y=m$.
Suy ra phương trình $\left| {{x}^{4}}-2{{x}^{2}} \right|=m$ có 4 nghiệm phân biệt khi và chỉ khi hai đồ thị có 4 giao điểm. Khi đó $m=1$. Chọn A.
| Bài tập 2: Tìm tất cả các giá trị của tham số $m$ để đường thẳng $y=m$ cắt đồ thị hàm số $y=\left| {{x}^{4}}-2{{x}^{2}}-2 \right|$ tại 6 điểm phân biệt.
A. $2<m<3$ B. $2<m<4$ C. $m=3$ D. $0<m<3$ |
Lời giải chi tiết

Vẽ đồ thị hàm số $y={{x}^{4}}-2{{x}^{2}}-2\left( C \right)$. Khi đó đồ thị hàm số $y=\left| {{x}^{4}}-2{{x}^{2}}-2 \right|$ gồm 2 phần:
Phần 1: Là phần đồ thị hàm số $\left( C \right)$ nằm phía bên trên trục hoành.
Phần 2: Lấy đối xứng phần của $\left( C \right)$ nằm dưới $Ox$ qua $Ox$.
Dựa vào đồ thị hàm số (hình vẽ bên) để đường thẳng $y=m$ cắt đồ thị $\left( C \right)$ tại 6 điểm phân biệt khi và chỉ khi $2<m<3$. Chọn A.
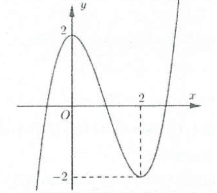
| Bài tập 3: Tìm tất cả các giá trị thực của tham số $m$ để phương trình $\left| 3x-{{x}^{3}}+1 \right|+m-2=0$ có sáu nghiệm phân biệt.
A. $1<m<2$ B. $0\le m\le 1$ C. $1\le m\le 2$ D. $0<m<1$ |
Lời giải chi tiết
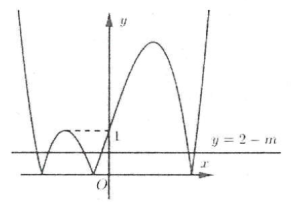
Ta có: PT $\Leftrightarrow \left| -{{x}^{3}}+3x+1 \right|=2-m\left( * \right)\Rightarrow $ Phương trình (*) là phương trình hoành độ giao điểm đồ thị hàm số $y=\left| 3x-{{x}^{3}}+1 \right|$ và đường thẳng $y=2-m$ vuông góc với trục tung. Phương trình đã cho có sáu nghiệm phân biệt khi và chỉ khi hai đồ thị cắt nhau tại 6 điểm phân biệt. Ta có đồ thị hai hàm số như hình bên. Để hai đồ thị cắt nhau tại 6 điểm thì $0<2-m<1\Leftrightarrow 1<m<2$. Chọn A.
| Bài tập 4: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình $\left| 2f\left( x \right)+1 \right|=5$ là: A. 3 B. 5 C. 2 D. 4 |
Lời giải chi tiết
Ta có: $\left| 2f\left( x \right)+1 \right|=5\Leftrightarrow \left[ \begin{array} {} 2f\left( x \right)+1=5 \\ {} 2f\left( x \right)+1=-5 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array} {} f\left( x \right)=2 \\ {} f\left( x \right)=-3 \\ \end{array} \right.$
Dựa vào đồ thị hàm số ta thấy, phương trình $f\left( x \right)=2$ có 2 nghiệm và phương trình $f\left( x \right)=-3$ có một nghiệm nên phương trình đã cho có 3 nghiệm. Chọn A.
| Bài tập 5: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình $\left| 2f\left( x \right)+3 \right|=8$ là: A. 7 B. 5 C. 4 D. 6 |
Lời giải chi tiết
Ta có: $\left| 2f\left( x \right)+3 \right|=8\Leftrightarrow \left[ \begin{array} {} 2f\left( x \right)+3=8 \\ {} 2f\left( x \right)+3=-8 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array} {} f\left( x \right)=\frac{5}{2} \\ {} f\left( x \right)=\frac{-11}{2} \\ \end{array} \right.$
Dựa vào đồ thị hàm số ta thấy, phương trình
![]()
có 4 nghiệm và phương trình $f\left( x \right)=\frac{-11}{2}$ có 2 nghiệm nên phương trình đã cho có 6 nghiệm. Chọn D.
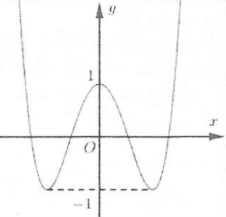
| Bài tập 6: Hình bên là đồ thị hàm số $y=2{{x}^{4}}-4{{x}^{2}}+1$.
Tìm tất cả các giá trị của tham số $m$ để phương trình $\left| {{x}^{4}}-2{{x}^{2}}+\frac{1}{2} \right|=2m$ có 8 nghiệm phân biệt A. $0<m<\frac{1}{2}$ B. $-\frac{1}{4}<m<\frac{1}{2}$ C. $0<m<\frac{1}{4}$ D. $m\ge \frac{1}{4}$ |
Lời giải chi tiết
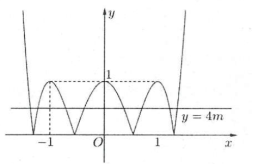
Ta có: PT $\Leftrightarrow \left| 2{{x}^{4}}-4{{x}^{2}}+1 \right|=4m$
Gọi $y=2{{x}^{4}}-4{{x}^{2}}+1\left( C \right)$
Đồ thị hàm số $y=\left| 2{{x}^{4}}-4{{x}^{2}}+1 \right|$ gồm 2 phần:
Phần 1: Là phần đồ thị hàm số $\left( C \right)$ nằm phía bên trên trục hoành.
Phần 2: Lấy đối xứng phần của $\left( C \right)$ nằm dưới $Ox$ qua $Ox$.
Dựa vào đồ thị hàm số $y=\left| 2{{x}^{4}}-4{{x}^{2}}+1 \right|$ và đường thẳng $y=4m$ suy ra phương trình đã cho có 8 nghiệm phân biệt khi và chỉ khi hai đồ thị có 8 giao điểm. Hai đồ thị có 8 giao điểm
$\Leftrightarrow 0<4m<1\Leftrightarrow 0<m<\frac{1}{4}$. Chọn C.
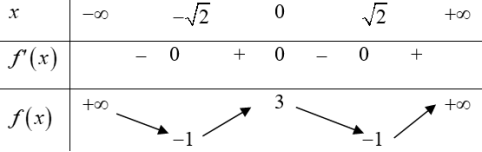
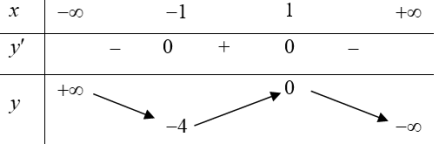
| Bài tập 7: Biết rằng hàm số $y={{x}^{4}}-4{{x}^{2}}+3$ có bảng biến thiên như sau:
Tìm $m$ để phương trình $\left| {{x}^{4}}-4{{x}^{2}}+3 \right|=m$ có đúng 4 nghiệm phân biệt. A. $1<m<3$ B. $m>3$ C. $m=0$ D. $m\in \left( 1;3 \right)\cup \left\{ 0 \right\}$ |
Lời giải chi tiết
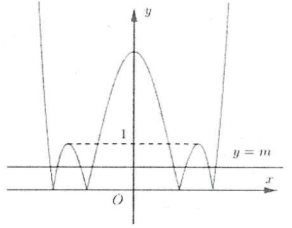
Vẽ đồ thị hàm số $y=\left| {{x}^{4}}-4{{x}^{2}}+3 \right|\left( {{C}'} \right)$
Ký hiệu $y={{x}^{4}}-4{{x}^{2}}+3\left( C \right)$ khi đó $\left( {{C}'} \right)$ gồm 2 phần:
Phần 1: Là phần của $\left( C \right)$ nằm trên trục $Ox$.
Phần 2: Lấy đối xứng phần của $\left( C \right)$ nằm dưới $Ox$ qua trục $Ox$
Để phương trình đã cho có 4 nghiệm phân biệt thì đường thẳng $y=m$ cắt $\left( C \right)$ tại 4 điểm phân biệt
$\Leftrightarrow \left[ \begin{array} {} m=0 \\ {} 1<m<3 \\ \end{array} \right.$. Chọn D.
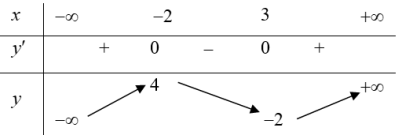
| Bài tập 8: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ.
Với $m\in \left( 1;3 \right)$ thì phương trình $\left| f\left( x \right) \right|=m$ có bao nhiêu nghiệm? A. 4 B. 3 C. 2 D. 5 |
Lời giải chi tiết
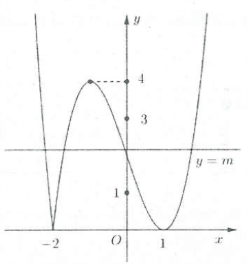
Phương trình $\left| f\left( x \right) \right|=m$ là phương trình hoành độ giao điểm của đồ thị hàm số $y=\left| f\left( x \right) \right|$ và đường thẳng $y=m$ song song trục hoành có đồ thị ở hình bên. Hai đồ thị có bao nhiêu giao điểm thì PT $\left| f\left( x \right) \right|=m$ có bấy nhiêu nghiệm.
$m\in \left( 1;3 \right)$ thì hai đồ thị có 4 giao điểm, suy ra PT $\left| f\left( x \right) \right|=m$ có 4 nghiệm. Chọn A.
| Bài tập 9: Cho hàm số $y=f\left( x \right)=\left( {{x}^{2}}+x-2 \right).g\left( x \right)$ có đồ thị như hình vẽ.
Gọi $S$ là tập hợp các giá trị nguyên của $m$ để phương trình $\left| {{x}^{2}}+x-2 \right|.g\left( x \right)=m$ có 3 nghiệm phân biệt. Tổng các phần tử của $S$ là: A. 4 B. 6 C. $-6$ D. $-4$ |
Lời giải chi tiết
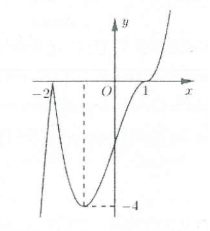
Ta có: ${{x}^{2}}+x-2\ge 0\Leftrightarrow \left[ \begin{array} {} x\ge 1 \\ {} x\le -2 \\ \end{array} \right.$
Gọi $y=f\left( x \right)=\left( {{x}^{2}}+x-2 \right).g\left( x \right)\left( C \right)$ thì đồ thị hàm số $y=\left| {{x}^{2}}+x-2 \right|.g\left( x \right)$ gồm 2 phần.
Phần 1: Là phần của $\left( C \right)$ ứng với miền $\left[ \begin{array} {} x\ge 1 \\ {} x\le -2 \\ \end{array} \right.$
Phần 2: Lấy đối xứng phần $\left( C \right)$ ứng với miền $-2<x<1$ qua trục hoành.
Dựa vào đồ thị hàm số suy ra phương trình $\left| {{x}^{2}}+x-2 \right|.g\left( x \right)=m$ có 3 nghiệm phân biệt khi $-4<m<0$.
Kết hợp $m\in \mathbb{Z}$ $\Rightarrow m=\left\{ -3;-2;-1 \right\}\Rightarrow $ tổng các phần tử của $S$ là $-6$. Chọn C.
| Bài tập 10: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình $\left| f\left( x-1 \right) \right|=2$ là A. 4 B. 5 C. 2 D. 3 |
Lời giải chi tiết
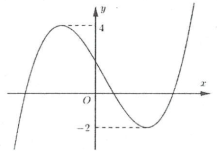
Ta có đồ thị hàm số $y=f\left( x \right)$ có dạng như hình sau:
Đồ thị hàm số $y=f\left( x-1 \right)\left( C \right)$ là đồ thị hàm số $y=f\left( x \right)$ khi dịch sang phải 1 đơn vị (xem hình 1).
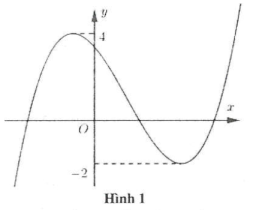
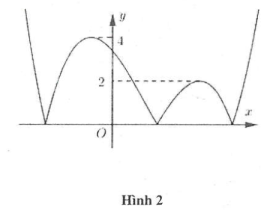
Đồ thị hàm số $y=\left| f\left( x-1 \right) \right|$ là gồm 2 phần (xem hình 2)
Phần 1: Là phần của $\left( C \right)$ nằm trên trục hoành
Phần 2: Lấy đối xứng phần nằm dưới trục hoành của $\left( C \right)$ qua $Ox$.
Dựa vào đồ thị hàm số $y=\left| f\left( x-1 \right) \right|$ suy ra phương trình $\left| f\left( x-1 \right) \right|=2$ có 5 nghiệm. Chọn B.
| Bài tập 11: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.
Phương trình $\left| f\left( x+1 \right) \right|=m$ có nhiều nghiệm nhất khi: A. $m=\frac{7}{2}$ B. $1<m<\frac{7}{2}$ C. $m=1$ D. $0<m<1$ |
Lời giải chi tiết
Đồ thị hàm số $y=f\left( x+1 \right)\left( C \right)$ là đồ thị hàm số $y=f\left( x \right)$ khi dịch sang trái 1 đơn vị (xem hình 1)
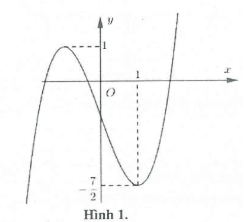 |
 |
Đồ thị hàm số $y=\left| f\left( x+1 \right) \right|$ gồm 2 phần (xem hình 2)
Phần 1: Là phần của $\left( C \right)$ nằm trên trục hoành
Phần 2: Lấy đối xứng phần nằm dưới trục hoành của $\left( C \right)$ qua $Ox$.
Dựa vào đồ thị hàm số $y=\left| f\left( x+1 \right) \right|$ suy ra phương trình $\left| f\left( x+1 \right) \right|=m$ có nhiều nghiệm nhất là 6 nghiệm khi $0<m<1$. Chọn D.
| Bài tập 12: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của $m$ để phương trình $f\left( \left| x \right|-1 \right)=m$ có 4 nghiệm phân biệt A. 3 B. 4 C. 5 D. 6 |
Lời giải chi tiết
Đồ thị hàm số $y=f\left( x-1 \right)\left( C \right)$ là đồ thị hàm số $y=f\left( x \right)$ khi dịch sang phải 1 đơn vị (hình 1)
Đồ thị hàm số $y=f\left( \left| x \right|-1 \right)$ gồm 2 phần:
Phần 1: Là phần của $\left( C \right)$ nằm bên phải trục tung.

Phần 2: Hàm số $y=f\left( \left| x \right|-1 \right)$ là hàm chẵn, ta lấy đối xứng phần 1 qua trục tung (hình 2).
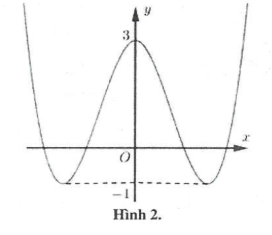
Dựa vào hình 2 suy ra phương trình $f\left( \left| x \right|-1 \right)=m$ có 4 nghiệm phân biệt khi $-1<m<3$
Với $m\in \mathbb{Z}\Rightarrow m=\left\{ 0;1;2 \right\}$. Chọn A.
TOÁN LỚP 12