Bài tập biện luận số nghiệm của phương trình bằng bảng biến thiên và đồ thị

Bài tập biện luận số nghiệm của phương trình bằng bảng biến thiên và đồ thị
Bài toán: Biện luận số nghiệm của phương trình: $F\left( x;m \right)=0$ theo tham số $m$ dựa vào đồ thị hoặc bảng biến thiên của hàm số $y=f\left( x \right)$.
Phương pháp giải cho bảng biến thiên tìm số nghiệm của phương trình
§ Bước 1: Biến đổi phương trình $F\left( x;m \right)=0$ về dạng $f\left( x \right)=g\left( m \right)$.
§ Bước 2: Vẽ đồ thị hoặc bảng biến thiên của hàm số $y=f\left( x \right)\left( C \right)$ và đường thẳng $d:y=g\left( m \right)$
Đường thẳng $d$ có đặc điểm vuông góc với trục tung và cắt trục tung tại điểm có tung độ $g\left( m \right)$.
§ Bước 3: Dựa vào đồ thị hoặc bảng biến thiên của hàm số để biện luận số nghiệm của phương trình đã cho.
Bài tập trắc nghiệ biện luận số nghiệm của phương trình có đáp án
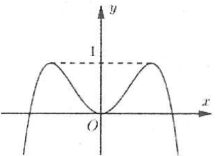
| Bài tập 1: Cho hàm số $y=-{{x}^{4}}+2{{x}^{2}}$ có đồ thị như hình bên.
Tìm tất cả các giá trị thực của tham số $m$để phương trình $-{{x}^{4}}+2{{x}^{2}}=m$ có bốn nghiệm thực phân biệt? A. $m>0$ B. $0\le m\le 1$ C. $0<m<1$ D. $m<1$ |
Lời giải chi tiết
Số nghiệm của phương trình phụ thuộc vào số giao điểm của đồ thị hàm số $y=-{{x}^{4}}+2{{x}^{2}}$ và đường thẳng $y=m$. Dựa vào hình vẽ suy ra phương trình đã cho có 4 nghiệm khi $0<m<1$. Chọn C.
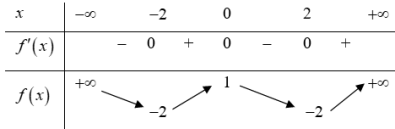
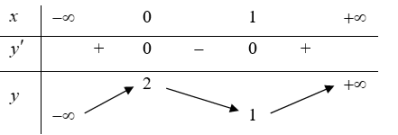
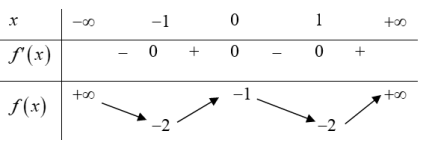
| Bài tập 2: [Đề thi tham khảo THPT QG năm 2019] Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
Số nghiệm thực của phương trình $2f\left( x \right)+3=0$ là A. 4 B. 3 C. 2 D. 1 |
Lời giải chi tiết
Số nghiệm thực của phương trình $f\left( x \right)+3=0\Leftrightarrow f\left( x \right)=\frac{-3}{2}$ chính là số giao điểm của đồ thị hàm số $y=f\left( x \right)$ và đường thẳng $y=-\frac{3}{2}$.
Đường thẳng $y=-\frac{3}{2}$ cắt đồ thị hàm số $y=f\left( x \right)$ tại 4 điểm phân biệt.
Vậy phương trình $2f\left( x \right)+3=0$ có đúng 4 nghiệm thực phân biệt. Chọn A.
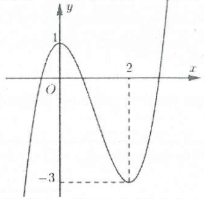
| Bài tập 3: Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị trong hình bên.
Hỏi phương trình $a{{x}^{3}}+b{{x}^{2}}+cx+d+1=0$ có bao nhiêu nghiệm? A. Phương trình không có nghiệm. B. Phương trình có đúng 1 nghiệm. C. Phương trình có đúng 2 nghiệm. D. Phương trình có đúng 3 nghiệm. |
Lời giải chi tiết
Số nghiệm của phương trình đã cho phụ thuộc vào số giao điểm của đồ thị hàm số
$y=a{{x}^{3}}+b{{x}^{2}}+cx+d\left( C \right)$ và đường thẳng $y=-1$.
Dựa vào đồ thị ta thấy $\left( C \right)$ cắt đường thẳng $y=-1$ tại 3 điểm phân biệt nên phương trình đã cho có 3 nghiệm. Chọn D.
| Bài tập 4: Tìm tất cả các giá trị $m$để phương trình ${{x}^{3}}-3x=2m$ có 3 nghiệm phân biệt
A. $-2<m<2$ B. $-1<m<1$ C. $-2\le m\le 2$ D. $-1\le m\le 1$ |
Lời giải chi tiết
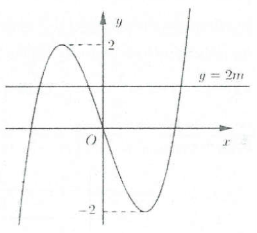
Phương trình ${{x}^{3}}-3x=2m$ là phương trình hoành độ giao điểm của đồ thị hàm số $y={{x}^{3}}-3x$ và đường thẳng $y=2m$. Phương trình có 3 nghiệm phân biệt khi hai đồ thị có ba giao điểm. Khi đó $-2<2m<2\Leftrightarrow -1<m<1$. Chọn B.
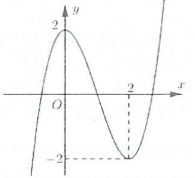
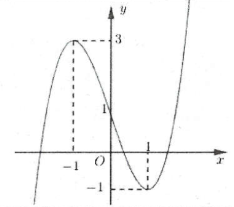
| Bài tập 5: [Đề thi THPT QG năm 2018] Cho hàm số $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\left( a,b,c,d\in \mathbb{R} \right)$.
Đồ thị của hàm số $y=f\left( x \right)$ như hình vẽ. Số nghiệm thực của phương trình $3f\left( x \right)+4=0$ là: A. 3 B. 0 C. 1 D. 2 |
Lời giải chi tiết
Ta có: $3f\left( x \right)+4=0\Leftrightarrow f\left( x \right)=\frac{-4}{3}$
Số nghiệm của phương trình $f\left( x \right)=-\frac{4}{3}$ là số giao điểm của đồ thị hàm số $y=f\left( x \right)$ và đường thẳng $y=-\frac{4}{3}$.
Dựa vào đồ thị hàm số suy ra phương trình $f\left( x \right)=-\frac{4}{3}$ có 3 nghiệm phân biệt. Chọn A.
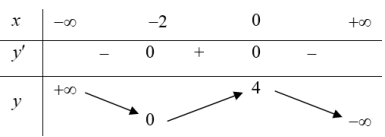
| Bài tập 6: Cho hàm số $y=f\left( x \right)=2{{x}^{3}}-3{{x}^{2}}+2$ có bảng biến thiên như sau:
Giá trị của tham số $m$ để phương trình ${{x}^{3}}-\frac{3}{2}{{x}^{2}}+2m-1=0$ có 3 nghiệm phân biệt là: A. $\frac{1}{2}<m<\frac{3}{4}$ B. $1<m<\frac{3}{2}$ C. $1<m<2$ D. $\frac{1}{2}<m<\frac{3}{2}$ |
Lời giải chi tiết
Ta có: PT $\Leftrightarrow 2{{x}^{3}}-3{{x}^{2}}+4m-2=0\Leftrightarrow 2{{x}^{3}}-3{{x}^{2}}+2=4-4m\left( 1 \right)$
Số nghiệm của phương trình (1) là số giao điểm của đồ thị $\left( C \right)$ và đường thẳng $d:y=4-4m$. Do vậy phương trình (1) có đúng 3 nghiệm khi $d$ cắt $\left( C \right)$ tại đúng 3 điểm phân biệt
$1<4-4m<2\Leftrightarrow \frac{1}{2}<m<\frac{3}{4}$. Chọn A.
| Bài tập 7: Cho hàm số $y=f\left( x \right)={{x}^{4}}-2{{x}^{2}}+2$ có bảng biến thiên như sau:
Số giá trị nguyên của $m$ để phương trình $2{{x}^{4}}-4{{x}^{2}}+m-5=0$ có đúng 2 nghiệm A. 3 B. 4 C. 5 D. 6 |
Lời giải chi tiết
Ta có: PT $\Leftrightarrow {{x}^{4}}-2{{x}^{2}}=\frac{5-m}{2}\Leftrightarrow {{x}^{4}}-2{{x}^{2}}+2=\frac{9-m}{2}\left( 2 \right)$
Số nghiệm của phương trình (2) là số giao điểm của đồ thị $\left( C \right)$ và đường thẳng $y=\frac{9-m}{2}$
Do vậy phương trình đã cho có 2 nghiệm $\Leftrightarrow $ $d$ cắt $\left( C \right)$ tại 2 điểm phân biệt
$\Leftrightarrow \left[ \begin{array} {} \frac{9-m}{2}=1 \\ {} \frac{9-m}{2}>2 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array} {} m=7 \\ {} m<5 \\ \end{array} \right.$
Kết hợp $m\in {{\mathbb{Z}}^{+}}\Rightarrow m=\left\{ 1;2;3;4;5;7 \right\}$. Chọn D.
| Bài tập 8: Tìm tất cả các giá trị thực của tham số $m$ sao cho đường thẳng $y=m$ cắt đồ thị hàm số $y={{x}^{3}}-3x+1$ tại 3 điểm phân biệt, trong đó có đúng hai điểm phân biệt có hoành độ dương.
A. $-1<m<3$ B. $1<m<3$ C. $-1<m<1$ D. $m=1$ |
Lời giải chi tiết
Ta có đồ thị hai hàm số như hình bên.
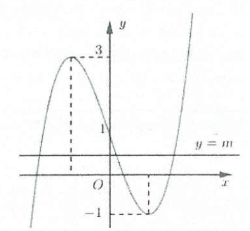
Đường thẳng $y=m$ cắt đồ thị hàm số $y={{x}^{3}}-3x+1$ tại 3 điểm phân biệt, trong đó có đúng hai điểm phân biệt có hoành độ dương khi và chỉ khi $-1<m<1$. Chọn C.
| Bài tập 9: Các giá trị $m$ để đường thẳng $y=m$ cắt đồ thị hàm số $y=\frac{1}{2}{{x}^{4}}-{{x}^{2}}+3$ tại 4 điểm phân biệt là
A. $\frac{5}{2}<m<3$ B. $\frac{1}{2}<m<3$ C. $m>3$ D. $\frac{1}{2}<m<\frac{5}{2}$ |
Lời giải chi tiết
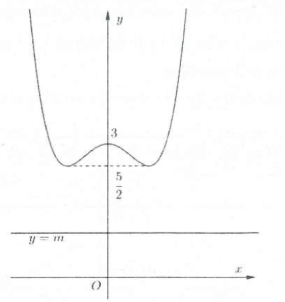
Ta có đồ thị hai hàm số $y=\frac{1}{2}{{x}^{4}}-{{x}^{2}}+3$ như hình bên. Dựa vào đồ thị ta thấy, đường thẳng $y=m$ cắt đồ thị hàm số $y=\frac{1}{2}{{x}^{4}}-{{x}^{2}}+3$ tại 4 điểm phân biệt khi và chỉ khi giá trị $m$ thuộc đoạn $\left( \frac{5}{2};3 \right)\Leftrightarrow \frac{5}{2}<m<3$. Chọn A.
| Bài tập 10: Đồ thị sau đây là của hàm số $y={{x}^{3}}-3x+1$.
Tìm $m$ để phương trình ${{x}^{3}}-3x-m=0$ có ba nghiệm phân biệt A. $-1<m<3$ B. $-2<m<2$ C. $-2\le m<2$ D. $-2<m<3$ |
Lời giải chi tiết
PT $\Leftrightarrow {{x}^{3}}-3x+1=m+1$. Số nghiệm của phương trình đã cho là số giao điểm đồ thị hàm số $y={{x}^{3}}-3x+1$ và đường thẳng $y=m+1$.
Dựa vào đồ thị ta thấy, phương trình có ba nghiệm phân biệt khi và chỉ khi hai đồ thị có ba giao điểm. Khi đó $-1<m+1<3\Leftrightarrow -2<m<2$. Chọn B.
| Bài tập 11: Cho hàm số $y=f\left( x \right)=-{{x}^{3}}-3{{x}^{2}}+4$ có bảng biến thiên như sau
Phương trình ${{x}^{3}}+3{{x}^{2}}+2m=0$, với $m$ là tham số thực, có 3 nghiệm thực phân biệt khi $m$ thuộc tập hợp nào dưới đây? A. $\left[ -2;0 \right]$ B. $\left( -2;0 \right)$ C. $\left[ -3;-2 \right]$ D. $\left[ -2;0 \right]$ |
Lời giải chi tiết
PT $\Leftrightarrow -{{x}^{3}}-3{{x}^{2}}+4=2m+4\left( * \right)$. Phương trình (*) là phương trình hoành độ giao điểm của đường thẳng $y=2m+4$ và đồ thị hàm số $y=f\left( x \right)=-{{x}^{3}}-3{{x}^{2}}+4$. PT có 3 nghiệm phân biệt khi hay đồ thị có 3 giao điểm.
Khi đó $0<2m+4<4\Leftrightarrow -2<m<0\Rightarrow m\in \left( -2;0 \right)$. Chọn B.
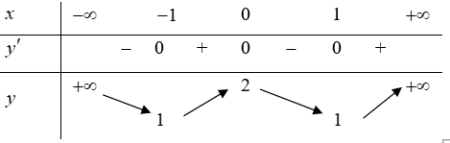
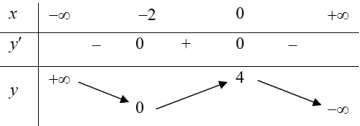
| Bài tập 12: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây
Tập hợp các giá trị của tham số $m$để phương trình $f\left( x \right)=m$ có bốn nghiệm phân biệt là A. $\left( -2;+\infty \right)$ B. $\left[ -2;-1 \right]$ C. $\left( -2;-1 \right)$ D. $\left( -\infty ;-1 \right)$ |
Lời giải chi tiết
Phương trình $f\left( x \right)=m$ là phương trình hoành độ giao điểm đồ thị hàm số $y=f\left( x \right)$ và đường thẳng $y=m$ song song trục hoành. Phương trình $f\left( x \right)=m$ có bốn nghiệm phân biệt khi và chỉ khi đường thẳng $y=m$ cắt đồ thị hàm số $y=f\left( x \right)$ tại 4 điểm phân biệt. Khi đó
$-2<m<1\Leftrightarrow m\in \left( 2;-1 \right)$. Chọn C.
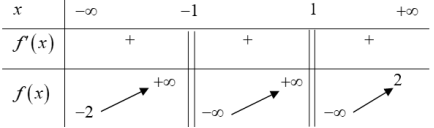
| Bài tập 13: Hàm số $y=f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1;1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
Tìm tất cả các giá trị thực của tham số $m$ để phương trình $f\left( x \right)=m$ có 3 nghiệm thực phân biệt. A. $m\in \left( 2;+\infty \right)$ B. $m\in \left( -\infty ;-2 \right)$ C. $m\in \left[ -2;2 \right]$ D. $m\in \left( -2;2 \right)$ |
Lời giải chi tiết
Phương trình $f\left( x \right)=m$ có 3 nghiệm thực phân biệt khi $m\in \left( -2;2 \right)$. Chọn D.
| Bài tập 14: Cho hàm số $y=f\left( x \right)=-{{x}^{3}}-3{{x}^{2}}+4$ có bảng biến thiên như sau
Phương trình ${{x}^{3}}+3{{x}^{2}}+2m=0$, với $m$ là tham số thực, có 3 nghiệm thực phân biệt khi $m$ thuộc tập hợp nào dưới đây? A. $\left[ -2;0 \right]$ B. $\left( -2;0 \right)$ C. $\left[ -3;-2 \right]$ D. $\left[ -2;0 \right]$ |
Lời giải chi tiết
PT $\Leftrightarrow -{{x}^{3}}-3{{x}^{2}}+4=2m+4\left( * \right)$. Phương trình (*) là phương trình hoành độ giao điểm của đường thẳng $y=2m+4$ và đồ thị hàm số $y=f\left( x \right)=-{{x}^{3}}-3{{x}^{2}}+4$. Phương trình có 3 nghiệm phân biệt khi hai đồ thị có 3 giao điểm. Khi đó $0<2m+4<4\Leftrightarrow -2<m<0\Rightarrow m\in \left( -2;0 \right)$. Chọn B.
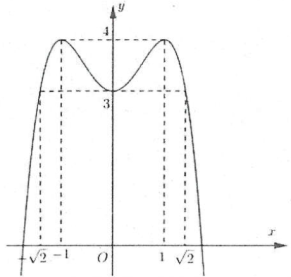
| Bài tập 15: Cho đồ thị hàm số $y=f\left( x \right)=-{{x}^{4}}+2{{x}^{2}}+3$ như hình vẽ.
Số các giá trị nguyên của tham số $m\in \left[ -10;10 \right]$ để phương trình ${{x}^{4}}-2{{x}^{2}}={{m}^{4}}-2{{m}^{2}}$ có đúng 2 nghiệm phân biệt là A. 17 B. 18 C. 19 D. 20 |
Lời giải chi tiết
Ta có: ${{x}^{4}}-2{{x}^{2}}={{m}^{4}}-2{{m}^{2}}\Leftrightarrow -{{x}^{4}}+2{{x}^{2}}+3=-{{m}^{4}}+2{{m}^{2}}+3\left( * \right)$
Dựa vào đồ thị hàm số ta thấy: Phương trình (*) có đúng hai nghiệm phân biệt $\Leftrightarrow -{{m}^{4}}+2{{m}^{2}}+3<3\Leftrightarrow \left[ \begin{array} {} m<-\sqrt{2} \\ {} m>\sqrt{2} \\ \end{array} \right.$
Kết hợp $\left\{ \begin{array} {} m\in \left[ -10;10 \right] \\ {} m\in \mathbb{Z} \\ \end{array} \right.\Rightarrow $ có 18 giá trị của tham số $m$. Chọn B.
| Bài tập 16: Cho hàm số $y={{x}^{3}}-6{{x}^{2}}+9x+m$ (với $m$ là tham số thực) có đồ thị $\left( C \right)$. Giả sử $\left( C \right)$ cắt trục hoành tại 3 điểm phân biệt có hoành độ ${{x}_{1}},\,\,{{x}_{2}},\,\,{{x}_{3}}$ (với ${{x}_{1}}<{{x}_{2}}<{{x}_{3}}$). Khẳng định nào sau đây đúng?
A. $0<{{x}_{1}}<1<{{x}_{2}}<3<{{x}_{3}}<4$ B. $1<{{x}_{1}}<{{x}_{2}}<3<{{x}_{3}}<4$ C. $1<{{x}_{1}}<3<{{x}_{2}}<4<{{x}_{3}}$ D. ${{x}_{1}}<0<1<{{x}_{2}}<3<{{x}_{3}}<4$ |
Lời giải chi tiết
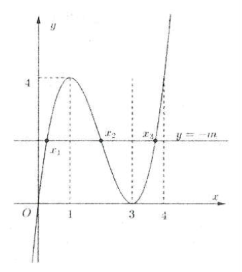
Đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm phân biệt.
Khi đó PT ${{x}^{3}}-6{{x}^{2}}+9x+m=0$ có ba nghiệm phân biệt.
Suy ra PT ${{x}^{3}}-6{{x}^{2}}+9x=-m$ có ba nghiệm phân biệt, suy ra đường thẳng $y=-m$ cắt đồ thị hàm số $y={{x}^{3}}-6{{x}^{2}}+9x$ tại 3 điểm phân biệt.
Ta có đồ thị hai hàm số như hình bên.
Hai đồ thị có 3 giao điểm khi và chỉ khi $-4<m<0$.
Khi đó $0<{{x}_{1}}<1<{{x}_{2}}<3<{{x}_{3}}<4$. Chọn A.
TOÁN LỚP 12