7 Dạng bài tập cực trị số phức thường gặp trong kì thi THPT quốc gia có đáp án chi tiết

7 Dạng bài tập cực trị số phức thường gặp trong kì thi THPT quốc gia có đáp án

@ Dạng 1: Cho số phức $z$ thỏa mãn $\left| z-{{z}_{1}} \right|=\left| z-{{z}_{2}} \right|$. Tìm số phức thỏa mãn $\left| z-{{z}_{0}} \right|$nhỏ nhất.

Phương pháp: Đặt $M(z);A({{z}_{1}});B({{z}_{2}})$là các điểm biểu diễn số phức $z;\,\,{{z}_{1}}$ và ${{z}_{2}}$. Khi đó từ giả thiết $\left| z-{{z}_{1}} \right|=\left| z-{{z}_{2}} \right|$suy ra $MA=MB$, tập hợp điểm biểu diễn số phức $z$ là đường trung trực ∆ của AB.

Gọi $N({{z}_{0}})$là  điểm biểu diễn số phức ${{z}_{0}}$

Ta có $MN=\left| z-{{z}_{0}} \right|$nhỏ nhất khi $M{{N}_{\min }}$ khi M là hình chiếu vuông góc của  N  trên  d  và $M{{N}_{\min }}=d(N;\Delta )$

Bài tập 1: Cho số phức $z$ thỏa mãn $\left| z-4-i \right|=\left| z+i \right|$. Gọi $z=a+bi\,\,(a;b\in \mathbb{R})$ là số phức thỏa mãn $\left| z-1+3i \right|$ nhỏ nhất. Giá trị của biểu thức $T=2a+3b$là: A. $-4$ B. 4 C. 0 D. 1

Lời giải chi tiết

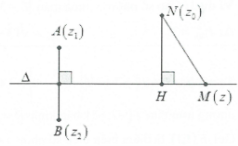Đặt $M(z);\,\,A(4;1),\,\,B(0;-1)$ là các điểm biểu diễn số phức $z;\,\,4+i$ và $-i$. Khi đó từ giả thiết suy ra $MA=MB$, tập hợp điểm biểu diễn số phức $z$ là đường trung trực của AB đi qua $I(2;0)$ và có VTPT là $\overrightarrow{n}=\overrightarrow{AB}(-4;-2)\Rightarrow \Delta :2x+y-4=0$

Gọi $N(1;-3)$là điểm biểu diễn số phức $1-3i$

Ta có $\left| z-1+3i \right|$ nhỏ nhất khi $M{{N}_{\min }}$ khi M  là hình chiếu vuông góc của N  trên ∆, suy ra $MN:x-2y+1=0$

Giải hệ $\left\{ \begin{array}  {} 2x+y-4=0 \\  {} x-2y-7=0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} x=3 \\  {} y=-2 \\ \end{array} \right.\Rightarrow M\left( 3;-2 \right)\Rightarrow z=3-2i\Rightarrow 2a+3b=0$. Chọn C.

Bài tập 2: Cho các số phức $z$ thỏa mãn $\left| z-2i \right|=\left| z+2 \right|$. Gọi $z$ là số phức thỏa mãn $\left| (2-i)z+5 \right|$nhỏ nhất. Khi đó : A. $0<\left| z \right|<1$ B. $1<\left| z \right|<2$ C. $2<\left| z \right|<3$ D. $\left| z \right|>3$

Lời giải chi tiết

Gọi $M(x;y);A(0;2),B(-2;0)$là các điểm biểu diễn số phức $z;\,\,2i$ và $-2$.

Từ giả thiết $\Rightarrow$$MA=MB\Rightarrow M\in$trung trực của AB có phương trình $\Delta :x+y=0$

Lại có: $P=\left| (2-i)z+5 \right|=\left| 2-i \right|\left| z+\frac{5}{2-i} \right|=\sqrt{5}\left| z+2+i \right|$, gọi $N(-2;-1)$là điểm biểu diễn số phức $-2-i$ suy ra $P=\sqrt{5}MN$

Ta có P nhỏ nhất khi $M{{N}_{\min }}$ khi M là hình chiếu vuông góc của N trên ∆, suy ra phương trình $MN:x-y+1=0$

Giải hệ $\left\{ \begin{array}  {} x+y=0 \\  {} x-y+1=0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} x=\frac{-1}{2} \\  {} y=\frac{1}{2} \\ \end{array} \right.\Rightarrow M\left( \frac{-1}{2};\frac{1}{2} \right)\Rightarrow z=\frac{-1}{2}+\frac{1}{2}i\Rightarrow \left| z \right|=\frac{\sqrt{2}}{2}$. Chọn A.

@ Dạng 2: Cho số phức $z$ thỏa mãn$\left| z-{{z}_{0}} \right|=R$. Tìm số phức thỏa mãn $P=\left| z-{{z}_{1}} \right|$đạt giá trị lớn nhất, nhỏ nhất.

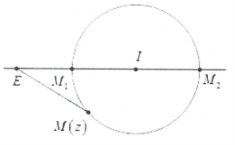
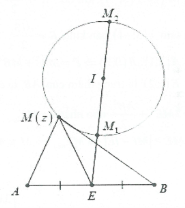
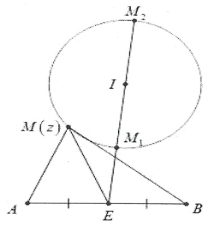
Phương pháp: Đặt $M(z);I({{z}_{0}});E({{z}_{1}})$ là các điểm biểu diễn số phức $z;\,\,{{z}_{0}}$ và ${{z}_{1}}$. Khi đó từ giả thiết $\left| z-{{z}_{0}} \right|=R\Leftrightarrow MI=R$ $\Rightarrow M$ thuộc đường tròn tâm I bán kính R. Ta có: $P=ME$ lớn nhất $\Leftrightarrow M{{E}_{max}}$và P nhỏ nhất $\Leftrightarrow M{{E}_{\min }}$. Khi đó:

${{P}_{max}}=IE+R\Leftrightarrow M\equiv {{M}_{2}}$và ${{P}_{\min }}=\left| IE-R \right|\Leftrightarrow M\equiv {{M}_{1}}$

(Điểm E có thể nằm trong hoặc ngoài đường tròn).

Bài tập 1: Cho số phức $z$thỏa mãn $\left| iz-3+2i \right|=3$. Tìm giá trị nhỏ nhất của biểu thức: $P=\left| z-1-i \right|$ A. ${{P}_{\min }}=3$ B.${{P}_{\min }}=\sqrt{13}-3$ C. ${{P}_{\min }}=2$              D. ${{P}_{\min }}=\sqrt{10}$

Lời giải chi tiết

Ta có: $\left| iz-3+2i \right|=3\Leftrightarrow \left| i \right|\left| z-\frac{3}{i}+2 \right|=3\Leftrightarrow \left| z+2+3i \right|=3\Rightarrow$ tập hợp điểm M biểu diễn số phức $z$là đường tròn tâm $I(-2;-3)$ bán kính $R=3$

Gọi $E(1;1)$ là điểm biểu diễn số phức $1+i\Rightarrow P=ME\Rightarrow {{P}_{\min }}=\left| EI-R \right|=2$

Bài tập 2: Cho số phức $z$ thỏa mãn $\left| z+2-i \right|=\sqrt{5}$. Gọi ${{z}_{1}}$ và ${{z}_{2}}$ lần lượt là 2 số phức làm cho biểu thức $P=\left| z-2-3i \right|$ đạt giá trị nhỏ nhất và lớn nhất. Tính $T=3\left| {{z}_{1}} \right|+2\left| {{z}_{2}} \right|$ A. $T=20$ B. $T=6$ C. $T=14$ D. $T=24$

Lời giải chi tiết

Ta có: $\left| z+2-i \right|=\sqrt{5}\Rightarrow$tập hợp điểm M  biểu diễn số phức $z$ là đường tròn tâm $I(-2;1)$ bán kính $R=\sqrt{5}$. Gọi $E(2;3)\Rightarrow P=ME$

Phương trình đường thẳng $IE:x-2y+4=0$

Dựa vào hình vẽ ta có ${{P}_{max}}=IE+R\Leftrightarrow M\equiv {{M}_{2}}$

Giải hệ $\left\{ \begin{array}  {} x-2y+4=0 \\  {} {{(x+2)}^{2}}+{{(y-1)}^{2}}=5 \\ \end{array} \right.\Rightarrow \left[ \begin{array}  {} {{M}_{2}}(-4;0)\Rightarrow {{P}_{\min }}=3\sqrt{5} \\  {} {{M}_{1}}(0;2)\Rightarrow {{P}_{\min }}=\sqrt{5} \\ \end{array} \right.$.

Do đó $T=3\left| {{z}_{1}} \right|+2\left| {{z}_{2}} \right|=3.2+2.4=14$. Chọn C.

@ Dạng 3: Cho số phức $z$ thỏa mãn $\left| z-{{z}_{1}} \right|=\left| z-{{z}_{2}} \right|$. Tìm số phức thỏa mãn $P=\left| z-{{z}_{3}} \right|+\left| z-{{z}_{4}} \right|$ đạt giá trị nhỏ nhất.

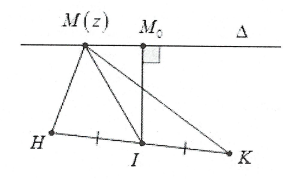
Phương pháp: Đặt $M(z);A({{z}_{1}});B({{z}_{2}});H({{z}_{3}});K({{z}_{4}})$ là các điểm biểu diễn số phức $z;{{z}_{1}};{{z}_{2}};{{z}_{3}}$và ${{z}_{4}}$. Khi đó từ giả thiết $\left| z-{{z}_{1}} \right|=\left| z-{{z}_{2}} \right|$ suy ra $MA=MB$, tập hợp điểm biểu diễn số phức $z$ là đường trung trực ∆ của AB; $P=\left| z-{{z}_{3}} \right|+\left| z-{{z}_{4}} \right|=MH+MK$

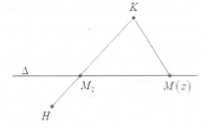
TH1: H, K nằm khác phía so với đường thẳng ∆

Ta có: $P=MH+MK\ge HK$

Dấu bằng xảy ra $\Leftrightarrow M\equiv {{M}_{o}}=HK\cap (\Delta )$

Khi đó ${{P}_{\min }}=HK$

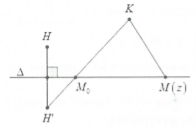TH2: H, K nằm cùng phía so với đường thẳng ∆

Gọi H’ là điểm đối xứng của ∆

Khi đó: $P=MH+MK=MH'+MK\ge H'K$

Dấu bằng xảy ra $\Leftrightarrow M\equiv {{M}_{o}}=H'K\cap (\Delta )$

Khi đó ${{P}_{\min }}=H'K$

Bài tập 1: Cho số phức $z$ thỏa mãn $\left| z-1+2i \right|=\left| z+3-2i \right|$. Gọi $z=a+bi$$(a;b\in \mathbb{R})$ sao cho $P=\left| z-2-4i \right|+\left| z+1-i \right|$ đạt giá trị nhỏ nhất. Khi đó $a+b$ là: A. 3 B. 5 C. 8 D. 4

Lời giải chi tiết

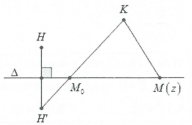Đặt $M(z);A(1;-2),B(-3;2)$ tử giả thiết suy ra $MA=MB$ nên M thuộc đường thẳng trung trực của AB có phương trình  $\Delta :x-y+1=0$, gọi $H(2;4)$và $K(-1;1)$ là các điểm biểu diễn số phức $2+4i$ và $-1+i$

Ta có $P=MH+MK$và 2 điểm H, K cùng phía so với đường thẳng ∆

Gọi H’ là điểm đối xứng của $\Delta :x-y+1=0$

Ta có: $HH':x+y-6=0$tọa độ trung điểm của HH’ là nghiệm hệ phương trình $\left\{ \begin{array}  {} x-y+1=0 \\  {} x+y-6=0 \\ \end{array} \right.\Rightarrow I\left( \frac{5}{2};\frac{7}{2} \right)$

Suy ra $H'(3;3)$

Lại có: $P=MH+MK=MH'+MK\ge H'K$

Dấu bằng xảy ra $\Leftrightarrow M=H'K\cap d$. Phương trình đường thẳng H’K là: $H'K:x-2y+3=0$

Suy ra ${{M}_{0}}=H'K\cap \Delta \Rightarrow {{M}_{o}}(1;2)\Rightarrow z=1+2i$. Khi đó ${{P}_{\min }}=H'K=2\sqrt{5}$. Chọn A.

Bài tập 2: Cho số phức $z$ thỏa mãn $\left| z-2+4i \right|=\left| iz-2 \right|$. Gọi $z=a+bi$$(a;b\in \mathbb{R})$ sao cho $P=\left| z-i \right|+\left| z+1+3i \right|$ đạt giá trị nhỏ nhất. Giá trị nhỏ nhất đấy bằng A. $\sqrt{53}$ B. $\sqrt{37}$ C. 4 D. $\sqrt{41}$

Lời giải chi tiết

Ta có:$\left| z-2+4i \right|=\left| iz-2 \right|\Leftrightarrow \left| z-2+4i \right|=\left| i \right|\left| z-\frac{2}{i} \right|=\left| z+2i \right|$

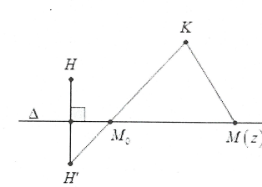Gọi $M(z);A(2;-4),B(0;-2)$từ giả thiết suy ra $MA=MB$ nên M thuộc đường thẳng trung trực của AB có phương trình  $\Delta :x-y-4=0$, gọi $H(0;1)$và $K(-1;-3)$là các điểm biểu diễn số phức $i$và $-1-3i$

Ta có: $P=MH+MK$và 2 điểm H, K cùng phía so với đường thẳng ∆

Gọi H’ là điểm đối xứng của $\Delta :x-y-5=0$

Ta có: $HH':x+y-1=0$ tọa độ trung điểm của HH’ là nghiệm hệ phương trình $\left\{ \begin{array}  {} x-y-4=0 \\  {} x+y-1=0 \\ \end{array} \right.\Rightarrow I\left( \frac{5}{2};-\frac{3}{2} \right)$

Suy ra $H'(5;-4)$

Lại có: $P=MH+MK=MH'+MK\ge H'K=\sqrt{37}$. Chọn B.

@ Dạng 4: Cho số phức $z$ thỏa mãn $\left| z-{{z}_{1}} \right|=\left| z-{{z}_{2}} \right|$. Tìm số phức thỏa mãn $P={{\left| z-{{z}_{3}} \right|}^{2}}+{{\left| z-{{z}_{4}} \right|}^{2}}$ đạt giá trị nhỏ nhất.

Phương pháp: Đặt x$M(z);A({{z}_{1}});B({{z}_{2}});H({{z}_{3}});K({{z}_{4}})$ là các điểm biểu diễn số phức $z;{{z}_{1}};{{z}_{2}};{{z}_{3}}$ và ${{z}_{4}}$. Khi đó từ giả thiết $\left| z-{{z}_{1}} \right|\equiv \left| z-{{z}_{2}} \right|$ suy ra $MA=MB$, tập hợp điểm biểu diễn số phức $z$ là đường trung trực ∆ của AB; $P={{\left| z-{{z}_{3}} \right|}^{2}}+{{\left| z-{{z}_{4}} \right|}^{2}}=M{{H}^{2}}+M{{K}^{2}}$

Gọi I là trung điểm của$HK\Rightarrow M{{I}^{2}}=\frac{M{{H}^{2}}+M{{K}^{2}}}{2}-\frac{H{{K}^{2}}}{4}\Rightarrow P=M{{H}^{2}}+M{{K}^{2}}=2M{{I}^{2}}+\frac{H{{K}^{2}}}{2}$

nhỏ nhất khi $M{{I}_{\min }}\Leftrightarrow M$ là hình chiếu vuông góc của I xuống$\Delta$.

Bài tập 1: Cho số phức $z$ thỏa mãn $\left| z+2-4i \right|=\left| z-2i \right|$. Gọi z là số phức thoả mãn biểu thức $P={{\left| z-i \right|}^{2}}+{{\left| z-4+i \right|}^{2}}$đạt giá trị nhỏ nhất. Tính${{\left| z \right|}^{2}}$. A. ${{\left| z \right|}^{2}}=12$ B. ${{\left| z \right|}^{2}}=10$ C. ${{\left| z \right|}^{2}}=2$              D. ${{\left| z \right|}^{2}}=5$

Lời giải chi tiết

Gọi $M(z);A(-2;4),B(0;2)$ là các điểm biểu diễn số phức$z;-2+4i$ và $2i$

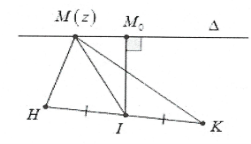
Khi đó $\left| z+2-4i \right|=\left| z-2i \right|\Leftrightarrow MA=MB\Rightarrow M$thuộc trung trực của AB có phương trình$\Delta :x-y+4=0$

Gọi$H\left( 0;1 \right),K\left( 4;-1 \right)\Rightarrow P=M{{H}^{2}}+M{{K}^{2}}=2M{{I}^{2}}+\frac{H{{K}^{2}}}{2}$

(với $I\left( 2;0 \right)$ là trung điểm của HK)

Do đó${{P}_{\min }}\Leftrightarrow M{{E}_{\min }}$ hay M là hình chiếu vuông góc của I xuống$\Delta$, khi đó

$IM:x+y-2=0\Rightarrow M=IM\cap \Delta \Rightarrow M\left( -1;3 \right)\Rightarrow {{\left| z \right|}^{2}}=O{{M}^{2}}=10$. Chọn B.

Bài tập 2: Cho số phức $z$ thỏa mãn $\left| z-1+3i \right|=\left| z+2+i \right|$. Giá trị nhỏ nhất của biểu thức $P={{\left| z-2+4i \right|}^{2}}+{{\left| z+2i \right|}^{2}}$ là: A. ${{P}_{\min }}=8$ B. ${{P}_{\min }}=9$ C. ${{P}_{\min }}=16$ D. ${{P}_{\min }}=25$

Lời giải chi tiết

Gọi $M(z);A(1;-3),B(-1;-1)$ là các điểm biểu diễn số phức$z;\,\,1+3i$ và $-1-i$

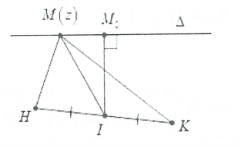
Khi đó$\left| z-1+3i \right|=\left| z+1+i \right|\Leftrightarrow MA=MB\Rightarrow M$thuộc trung trực của AB có phương trình$\Delta :x-y-2=0$

Gọi$H\left( 2;-4 \right),K\left( 0;-2 \right)\Rightarrow P=M{{H}^{2}}+M{{K}^{2}}=2M{{I}^{2}}+\frac{H{{K}^{2}}}{2}$

(với$I\left( 1;-3 \right)$là trung điểm của HK)

Do đó ${{P}_{\min }}\Leftrightarrow M{{E}_{\min }}$ hay M là hình chiếu vuông góc của I xuống$\Delta$, khi đó ${{P}_{\min }}=2{{\left[ d\left( I;\Delta  \right) \right]}^{2}}+\frac{H{{K}^{2}}}{2}=8$. Chọn A.

@ Dạng 5: Cho số phức $z$ thỏa mãn $\left| z-{{z}_{0}} \right|=R$. Tìm số phức thỏa mãn $P={{\left| z-{{z}_{1}} \right|}^{2}}+{{\left| z-{{z}_{2}} \right|}^{2}}$đạt giá trị lớn nhất, nhỏ nhất.

Phương pháp: Đặt$M(z);A({{z}_{1}});B({{z}_{2}});I\left( {{z}_{0}} \right)$ là các điểm biểu diễn số phức $z;{{z}_{1}};{{z}_{2}}$ và ${{z}_{0}}$.

Khi đó từ giả thiết $\left| z-{{z}_{0}} \right|=R\Leftrightarrow MI=R\Rightarrow M$thuộc đường tròn tâm I bán kính R.

Gọi E là trung điểm của AB ta có: $P=2M{{E}^{2}}+\frac{A{{B}^{2}}}{2}$ lớn nhất $\Leftrightarrow M{{E}_{\text{max}}}$và P nhỏ nhất$\Leftrightarrow M{{E}_{\text{min}}}$.

Khi đó${{P}_{max}}\Leftrightarrow M\equiv {{M}_{2}}$ và ${{P}_{\min }}\Leftrightarrow M\equiv {{M}_{1}}$.

 

Bài tập 1: Cho số phức $z$ thỏa mãn $\left| z-1+2i \right|=2$. Gọi$z=a+bi\left( a;b\in \mathbb{R} \right)$ là số thức thỏa mãn biểu thức $P={{\left| z-2-3i \right|}^{2}}+{{\left| z-5i \right|}^{2}}$ đạt giá trị lớn nhất. Tính $T=a+b$ A. $T=1$ B. $T=3$ C. $T=-1$ D. $T=-3$

Lời giải chi tiết

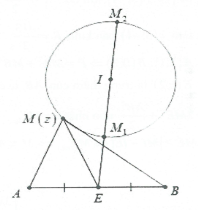
Gọi $M\left( z \right);I\left( 1;-2 \right)$ khi đó$MI=2\Leftrightarrow M$thuộc đường tròn tâm

$I\left( 1;-2 \right)$ bán kính $R=2$

Đặt $A\left( 2;3 \right);B\left( 0;5 \right)\Rightarrow P=M{{A}^{2}}+M{{B}^{2}}$

Gọi $H\left( 1;4 \right)$là trung điểm của AB ta có :

$P=2M{{H}^{2}}+\frac{A{{B}^{2}}}{2}$ lớn nhất$\Leftrightarrow M{{H}_{\text{max}}}$

Do $MH\le MI+IH\Leftrightarrow M{{H}_{\text{max}}}\Leftrightarrow M\equiv {{M}_{2}}$

Ta có:$IH:x=1$

Giải hệ$\left\{ \begin{array}  {} x=1 \\  {} {{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=4 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} {{M}_{1}}\left( 1;0 \right) \\  {} {{M}_{2}}\left( 1;-4 \right) \\ \end{array} \right.$. Do đó$a+b=-3$. Chọn D.

Bài tập 2: Cho số phức $z$ thỏa mãn $\left| z-3+i \right|=\frac{\sqrt{13}}{2}$. Gọi $z=a+bi\left( a;b\in \mathbb{R} \right)$ là số thức thỏa mãn biểu thức $P={{\left| z-2-i \right|}^{2}}+{{\left| z-3i \right|}^{2}}$ đạt giá trị nhỏ nhất. Tính $T=a+b$ A. $T=\frac{5}{2}$ B. $T=\frac{3}{2}$ C. $T=\frac{13}{2}$  D. $T=\frac{9}{2}$

Lời giải chi tiết

Gọi $M\left( z \right);I\left( 3;-1 \right)$khi đó$MI=\frac{\sqrt{13}}{2}\Leftrightarrow M$ thuộc đường tròn tâm $I\left( 3;-1 \right)$ bán kính $R=\frac{\sqrt{13}}{2}$

Đặt $A\left( 2;1 \right);B\left( 0;3 \right)\Rightarrow P=M{{A}^{2}}+M{{B}^{2}}$

Gọi $E\left( 1;2 \right)$là trung điểm của AB ta có :

$P=2M{{E}^{2}}+\frac{A{{B}^{2}}}{2}$nhỏ nhất$\Leftrightarrow M{{E}_{\text{min}}}$

Do $ME\ge \left| MI-IE \right|\Leftrightarrow M{{E}_{\text{min}}}\Leftrightarrow M\equiv {{M}_{1}}$

Ta có: $IE:3x+2y-7=0$. Giải hệ$\left\{ \begin{array}  {} 3x-2y-7=0 \\  {} {{\left( x-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=\frac{13}{4} \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} {{M}_{1}}\left( 2;\frac{1}{2} \right) \\  {} {{M}_{2}}\left( 4;\frac{-5}{2} \right) \\ \end{array} \right.$. Do đó$a+b=\frac{5}{2}$. Chọn A.

 Dạng 6: Cho hai số phức ${{z}_{1}};{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}}-{{z}_{0}} \right|=R$và $\left| {{z}_{2}}-{{\text{w}}_{1}} \right|=\left| {{z}_{2}}-{{\text{w}}_{2}} \right|$;

trong đó ${{z}_{0;}}{{\text{w}}_{1}};{{\text{w}}_{2}}$ là các số phức đã biết. Tìm giá trị nhỏ nhất của biểu thức$P=\left| {{z}_{1}}-{{\text{z}}_{2}} \right|$

Phương pháp: Đặt $M({{z}_{1}});N\left( {{z}_{2}} \right)$ lần lượt là các điểm biểu diễn số phức ${{z}_{1}}$và ${{z}_{2}}$.

Điểm M thuộc đường tròn tâm$I\left( {{z}_{0}} \right)$ bán kính$R$,$N$ thuộc trung trực $\Delta$ của AB với$A\left( {{\text{w}}_{1}} \right);B\left( {{\text{w}}_{2}} \right)$

Lại có: $P=MN\Rightarrow {{P}_{\min }}=\left| {{d}_{(t;\Delta )}}-R \right|$

 

f Ví dụ 1: Cho số phức ${{z}_{1}}$ thỏa mãn ${{\left| z-2 \right|}^{2}}-{{\left| z+i \right|}^{2}}=1$ và số phức ${{z}_{2}}$ thỏa mãn $\left| z-4-i \right|=\sqrt{5}$. Tìm giá trị nhỏ nhất của $\left| {{z}_{1}}-{{z}_{2}} \right|$ A. $\frac{2\sqrt{5}}{5}$ B. $\sqrt{5}$ C. $2\sqrt{5}$ D. $\frac{3\sqrt{5}}{5}$

Lời giải

Gọi $M(z;y)$là điểm biểu diễn số phức ${{z}_{1}}$. Khi đó ${{\left| z-2 \right|}^{2}}-{{\left| z+i \right|}^{2}}=1$

$\Leftrightarrow {{(x-2)}^{2}}+{{y}^{2}}-{{x}^{2}}-{{(y+1)}^{2}}=1\Leftrightarrow -4x-2y=-2\Leftrightarrow (\Delta ):2x+y-1=0$

Gọi $N(a;b)$là điểm biểu diễn số phức ${{z}_{2}}$. Khi đó $\left| z-4-i \right|=\sqrt{5}\Leftrightarrow {{(a-4)}^{2}}+{{(b-1)}^{2}}=5$

Hay tập hợp điểm N trong mặt phẳng Oxy là đường tròn $(C):{{(x-4)}^{2}}+{{(y-1)}^{2}}=5$

Ta có $d\left( {{I}_{(c)}};(\Delta ) \right)=\frac{8}{\sqrt{5}}>\sqrt{5}={{R}_{(C)}}$

$\Rightarrow \left( \Delta  \right)$ không cắt đường tròn$\left( C \right)$.

Lại có$MN=\left| {{z}_{1}}-{{z}_{2}} \right|\Rightarrow$dựa vào hình vẽ ta thấy

$M{{N}_{\min }}\Leftrightarrow MN=d\left( {{I}_{\left( C \right)}};\left( \Delta  \right) \right)-{{R}_{\left( C \right)}}$

Hay${{\left| {{z}_{1}}-{{z}_{2}} \right|}_{\min }}=\frac{8\sqrt{5}}{5}-\sqrt{5}=\frac{3\sqrt{5}}{5}$. Chọn D.

Bài toán có thể hỏi thêm là tìm số phức ${{z}_{1}}$ hoặc ${{z}_{2}}$ để${{\left| {{z}_{1}}-{{z}_{2}} \right|}_{\min }}$ thì ta chỉ cần viết phương trình đường thẳng$MN\bot \left( \Delta  \right)$ sau đó tìm giao điểm$\left\{ \begin{array}  {} M=\left( \Delta  \right)\cap MN \\  {} N=\left( C \right)\cap MN \\ \end{array} \right.$.

Ví dụ 2: Cho hai số phức ${{z}_{1}};{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}}+5 \right|=5$ và $\left| {{z}_{2}}+1-3i \right|=\left| {{z}_{2}}-3-6i \right|$. Tìm giá trị nhỏ nhất của biểu thức $P=\left| {{z}_{1}}-{{z}_{2}} \right|$ A. ${{P}_{\min }}=\frac{5}{2}$ B. ${{P}_{\min }}=\frac{15}{2}$ C. ${{P}_{\min }}=3$              D. ${{P}_{\min }}=10$

Lời giải

Gọi $M\left( {{z}_{1}} \right);N\left( {{z}_{2}} \right)$lần lượt là các điểm biểu diễn các số phức${{z}_{1}}$và${{z}_{2}}$.

Điểm M thuộc đường thẳng tròn tâm $I\left( -5;0 \right)$ bán kính $R=5$.

Điểm N thuộc đường thẳng trung trực $\Delta$ của AB với $A\left( -1;3 \right);B\left( 3;6 \right)\Rightarrow \Delta :4x+3y-\frac{35}{2}=0$

Lại có: $P=MN\Rightarrow {{P}_{min}}=\left| {{d}_{\left( I;\Delta  \right)}}-R \right|=\frac{5}{2}$. Chọn A.

 Dạng 7: Cho hai số phức ${{z}_{1}};{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}}-{{\text{w}}_{1}} \right|={{R}_{1}}$ và $\left| {{z}_{2}}-{{\text{w}}_{1}} \right|={{R}_{2}}$ trong đó${{\text{w}}_{1}};{{\text{w}}_{2}}$ là các số phức đã biết. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức$P=\left| {{z}_{1}}-{{z}_{2}} \right|$.

Phương pháp: Đặt $M({{z}_{1}});N\left( {{z}_{2}} \right)$lần lượt là các điểm biểu diễn số phức ${{z}_{1}}$và ${{z}_{2}}$.

Điểm M  thuộc đường tròn tâm $\left( {{C}_{1}} \right)$ tâm $I\left( {{\text{w}}_{1}} \right)$ bán kính ${{R}_{1}}$ và $N$ thuộc đường tròn $\left( {{C}_{2}} \right)$  tâm $K\left( {{\text{w}}_{2}} \right)$ bán kính ${{R}_{2}}\Rightarrow P=MN$. Dựa vào các vị trí tương đối của 2 đường tròn để tìm $M{{N}_{max}};M{{N}_{\min }}$

Ví dụ 1: Cho hai số phức $z;\text{w}$ thỏa mãn $z.\overline{z}=1$ và $\left| \text{w}-3+4i \right|=2$. Tìm giá trị lớn nhất của biểu thức $P=\left| z-\text{w} \right|$ A. ${{P}_{max}}=5$ B. ${{P}_{\text{max}}}=8$ C. ${{P}_{\text{max}}}=10$              D. ${{P}_{\text{max}}}=5+\sqrt{2}$

Lời giải

Ta có:$z.\overline{z}=1\Leftrightarrow \left| z \right|=1$

Gọi $M\left( z \right);N\left( \text{w} \right)$ lần lượt là các điểm biểu diễn các số phức $z$ và $\text{w}$.

Điểm M thuộc đường tròn tâm $\left( {{C}_{1}} \right)$ tâm $O\left( 0;0 \right)$ bán kính ${{R}_{1}}=1$ và $N$ thuộc đường tròn $\left( {{C}_{2}} \right)$  tâm $K(3;-4)$ bán kính ${{R}_{2}}=2\Rightarrow P=MN$.

Dễ thấy $OK=5>{{R}_{1}}+{{R}_{2}}$ nên $\left( {{C}_{1}} \right)$ và $\left( {{C}_{2}} \right)$ nằm ngoài nhau suy ra $M{{N}_{max}}=OK+{{R}_{1}}+{{R}_{2}}=8$. Chọn B.

Ví dụ 2: [Đề tham khảo Bộ GD {} ĐT 2018] Xét các số phức$z=a+bi\left( a,b\in \mathbb{R} \right)$ thỏa mãn điều kiện $\left| z-4-3i \right|=\sqrt{5}$. Tính $P=a+b$khi giá trị biểu thức $\left| z+1-3i \right|+\left| z-1+i \right|$ đạt giá trị lớn nhất A. $P=10$ B. $P=4$ C. $P=6$ D. $P=8$

 

Lời giải

Gọi$M\left( x;y \right)$là điểm biểu diễn số phức$z$

Từ giả thiết, ta có $\left| z-4-3i \right|=\sqrt{5}\Leftrightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=5\Rightarrow M$ thuộc đường tròn$\left( C \right)$tâm$I\left( 4;3 \right)$, bán kính $R=\sqrt{5}$. Khi đó $P=MA+MB$, với$A\left( -1;3 \right),B\left( 1;-1 \right)$.

Ta có ${{P}^{2}}=M{{A}^{2}}+M{{B}^{2}}+2MA.MB\le 2\left( M{{A}^{2}}+M{{B}^{2}} \right).$

Gọi $E\left( 0;1 \right)$là trung điểm$AB\Rightarrow M{{E}^{2}}=\frac{M{{A}^{2}}+M{{B}^{2}}}{2}-\frac{A{{B}^{2}}}{4}$.

Do đó ${{P}^{2}}\le 4.M{{E}^{2}}+A{{B}^{2}}$ mà $ME\le CE=3\sqrt{5}$ suy ra ${{P}^{2}}\le 4.{{\left( 3\sqrt{5} \right)}^{2}}+{{\left( 2\sqrt{5} \right)}^{2}}=200$.

Với C là giao điểm của đường thẳng EI với đường tròn$\left( C \right)$.

Vậy$P\le 10\sqrt{2}$. Dấu$''=''$ xảy ra$\left\{ \begin{array}  {} MA=MB \\  {} M\equiv C \\ \end{array} \right.\Rightarrow M\left( 6;4 \right)\Rightarrow a+b=10$. Chọn A.

Ví dụ 3: [Đề tham khảo Bộ GD {} ĐT 2017] Xét các số phức $z$ thỏa mãn điều kiện: $\left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của$\left| z-1+i \right|$. Tính $P=M+m$ A. $P=\sqrt{13}+\sqrt{73}$ B. $P=\frac{5\sqrt{2}+2\sqrt{73}}{2}$              C. $P=5\sqrt{2}+\sqrt{73}$              D. $P=\frac{5\sqrt{2}+\sqrt{73}}{2}$

Lời giải

Đặt $z=x+yi\left( x,y\in \mathbb{R} \right)$ và gọi

$M\left( x;y \right),A\left( -2;1 \right),B\left( 4;7 \right)$ suy ra $AB=6\sqrt{2}$.

Ta có $=\left( 6;6 \right)\Rightarrow =\left( 1;-1 \right)\Rightarrow$phương trình đường thẳng

AB là $x-y+3=0$.

Từ giả thiết, ta có $MA+MB=6\sqrt{2}\to MA+MB=AB$

suy ra M  thuộc đoạn thẳng  AB.

Gọi $N\left( 1;-1 \right)\Rightarrow \left| z-1+i \right|=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}=MN\Rightarrow \left\{ \begin{array}  {} {{\left| z-1+i \right|}_{min}}=M{{N}_{\min }} \\  {} {{\left| z-1+i \right|}_{\text{max}}}=M{{N}_{\text{max}}} \\ \end{array} \right.$.

 Độ dài đoạn thẳng MN nhỏ nhất khi và chỉ khi M là hình chiếu của N trên AB.

Hay $M{{N}_{\min }}=d\left( N;\left( AB \right) \right)=\frac{\left| 1-\left( -1 \right)+3 \right|}{\sqrt{{{1}^{2}}+{{\left( -1 \right)}^{2}}}}=\frac{5\sqrt{2}}{2}\to m=\frac{5\sqrt{2}}{2}$

 Độ dài đoạn thẳng MN lớn nhất khi và chỉ khi$M\equiv A$hoặc$M\equiv B$.

Ta có $\left\{ \begin{array}  {} M\equiv A\to MN=AN=\sqrt{13} \\  {} M\equiv B\to MN=BN=\sqrt{73} \\ \end{array} \right.\Rightarrow M{{N}_{max}}=\sqrt{73}\to M=\sqrt{73}.$

Vậy giá trị biểu thức $P=M+m=\frac{5\sqrt{2}+2\sqrt{73}}{2}$. Chọn B.

Ví dụ 4: Xét các số phức $z$ thỏa mãn điều kiện: $\left| z-1-i \right|+\left| z-7-4i \right|=3\sqrt{5}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $\left| z-5+2i \right|$. Tính $P=M+m$ A. $P=\sqrt{5}+\sqrt{10}$ B. $P=\frac{2\sqrt{5}+\sqrt{10}}{2}$              C. $P=2\left( \sqrt{5}+\sqrt{10} \right)$              D. $P=\frac{5\sqrt{2}+\sqrt{10}}{2}$

Lời giải

Đặt $z=x+yi\left( x,y\in \mathbb{R} \right)$ và gọi $M\left( x;y \right),A\left( 1;1 \right),B\left( 7;4 \right)$

suy ra $AB=3\sqrt{5}$.

Ta có$=\left( 6;3 \right)\Rightarrow {{}_{_{(AB)}}}=\left( 1;-2 \right)\Rightarrow$ phương trình đường

thẳng  AB  là $x-2y+1=0$.

Từ giả thiết, ta có $MA+MB=3\sqrt{5}\to MA+MB=AB$

suy ra  M  thuộc đoạn thẳng AB.

Gọi$N\left( 5;-2 \right)\Rightarrow \left| z-5+2i \right|=MN\Rightarrow \left\{ \begin{array}  {} {{\left| z-5+2i \right|}_{min}}=M{{N}_{\min }} \\  {} {{\left| z-5+2i \right|}_{max}}=M{{N}_{\text{max}}} \\ \end{array} \right.$.

 Độ dài đoạn thẳng MN nhỏ nhất khi và chỉ khi M là hình chiếu của N  trên AB.

Hay $M{{N}_{\min }}=d\left( N;\left( AB \right) \right)=\frac{\left| 5-2\left( -2 \right)+1 \right|}{\sqrt{{{1}^{2}}+{{\left( -2 \right)}^{2}}}}=2\sqrt{5}\to m=2\sqrt{5}$

 Độ dài đoạn thẳng MN lớn nhất khi và chỉ khi$M\equiv A$hoặc$M\equiv B$.

Ta có$\left\{ \begin{array}  {} M\equiv A\to MN=AN=5 \\  {} M\equiv B\to MN=BN=2\sqrt{10} \\ \end{array} \right.\Rightarrow M{{N}_{max}}=2\sqrt{10}\to M=2\sqrt{10}.$

Vậy giá trị biểu thức $P=M+m=2\left( \sqrt{5}+\sqrt{10} \right).$ Chọn C.

Ví dụ 5: Biết số phức $z$ thỏa mãn đồng thời hai điều kiện $\left| z-3-4i \right|=\sqrt{5}$và biểu thức $M={{\left| z+2 \right|}^{2}}-{{\left| z-i \right|}^{2}}$ đạt giá trị lớn nhất. Tính môđun của số phức $z+i$. A. $\left| z+i \right|=2\sqrt{41}$ B. $\left| z+i \right|=3\sqrt{5}$ C. $\left| z+i \right|=5\sqrt{2}$              D. $\left| z+i \right|=\sqrt{41}$

Lời giải

Gọi $z=x+yi\left( x,y\in \mathbb{R} \right)$

Ta có: $\left| z-3-4i \right|=\sqrt{5}\Leftrightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=5\Rightarrow$ tập hợp điểm biểu diễn số phức $z$ là dường tròn $\left( C \right)$ tâm $I\left( 3;4 \right)$ và $R=\sqrt{5}$.

Mặt khác: $M={{\left| z+2 \right|}^{2}}-{{\left| z-i \right|}^{2}}={{\left( x+2 \right)}^{2}}+{{y}^{2}}-\left[ \left( {{x}^{2}} \right)+{{\left( y-1 \right)}^{2}} \right]=4x+2y+3$$\Leftrightarrow d:4x+2y+3-M=0$

Do số phức $z$ thỏa mãn đồng thời hai điều kiện nên  d  và $\left( C \right)$ có điểm chung

$\Leftrightarrow d\left( I;d \right)\le R\Leftrightarrow \frac{\left| 23-M \right|}{2\sqrt{5}}\le \sqrt{5}\Leftrightarrow \left| 23-M \right|\le 10\Leftrightarrow 13\le M\le 33$

$\Rightarrow {{M}_{max}}=33\Leftrightarrow \left\{ \begin{array}  {} 4x+2y-30=0 \\  {} {{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=5 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} x=5 \\  {} y=-5 \\ \end{array} \right.\Rightarrow z+i=5-4i\Rightarrow \left| z+i \right|=\sqrt{41}$. Chọn D.

Ví dụ 6: Cho hai số phức ${{z}_{1}}$ và ${{z}_{2}}$ thỏa mãn ${{z}_{1}}+{{z}_{2}}=8+6i$ và $\left| {{z}_{1}}-{{z}_{2}} \right|=2$. Tìm giá trị lớn nhất của $P=\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|?$ A. $P=4\sqrt{6}$ B. $P=5+3\sqrt{5}$ C. $P=2\sqrt{26}$ D. $P=34+3\sqrt{2}$

Lời giải

Đặt $A\left( {{z}_{1}} \right);B\left( {{z}_{2}} \right)$theo giả thiết ta có: $\overrightarrow{OA}+\overrightarrow{OB}=(8;6);\left| - \right|=2;P=OA+OB$

$104={{\left( + \right)}^{2}}+{{\left( - \right)}^{2}}=2\left( O{{A}^{2}}+O{{B}^{2}} \right)\ge {{\left( OA+OB \right)}^{2}}={{P}^{2}}\Rightarrow P\le \sqrt{104}=2\sqrt{26}$. Chọn C.

Ví dụ 7: [Đề thi thử chuyên Đại học Vinh 2018] Giả sử ${{z}_{1}},{{z}_{2}}$ là hai trong các số phức $z$ thỏa mãn $\left| iz+\sqrt{2}-i \right|=1$ và $\left| {{z}_{1}}-{{z}_{2}} \right|=2$. Giá trị lớn nhất của $\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|$bằng A. 3 B. $2\sqrt{3}$ C. $3\sqrt{2}$  D. 4

Lời giải

Ta có:$\left| iz+\sqrt{2}-i \right|=1\Leftrightarrow \left| i\left( x+yi \right)+\sqrt{2}-i \right|=1$ (với$z=x+yi\left( x;y\in \mathbb{R} \right)$)

$\Leftrightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-\sqrt{2} \right)}^{2}}=1\Rightarrow M\left( x;y \right)$ biểu diễn $z$thuộc đường tròn tâm$I\left( 1;\sqrt{2} \right)$ bán kính $R=1$.

Giả sử $A\left( {{z}_{1}} \right);B\left( {{z}_{2}} \right)$ do $\left| {{z}_{1}}-{{z}_{2}} \right|=2\Rightarrow AB=2=2R$ nên $AB$ là đường kính của đường tròn$\left( I;R \right)$

Lại có:$\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|=OA+OB$

Mặt khác theo công thức trung tuyến ta có:$O{{I}^{2}}=\frac{O{{A}^{2}}+O{{B}^{2}}}{2}-\frac{A{{B}^{2}}}{4}\Rightarrow O{{A}^{2}}+O{{B}^{2}}=8$

Theo BĐT Bunhiascopky ta có: $2\left( O{{A}^{2}}+O{{B}^{2}} \right)\ge {{\left( OA+OB \right)}^{2}}\Rightarrow OA+OB\le 4$. Chọn D.

Ví dụ 8: Cho ${{z}_{1}},{{z}_{2}}$ là hai trong các số phức $z$ thỏa mãn điều kiện $\left| z-5-3i \right|=5$và $\left| {{z}_{1}}-{{z}_{2}} \right|=8$. Giá trị nhỏ nhất của biểu thức $\left| {{z}_{1}}+{{z}_{2}} \right|$là: A. $6-\sqrt{34}$ B. $2\sqrt{34}-6$ C. $2\sqrt{34}+6$  D. $\sqrt{34}+6$

Lời giải

Giả sử $\text{w}={{z}_{1}}+{{z}_{2}}$

Đặt$\left\{ \begin{array}  {} {{\text{w}}_{1}}={{z}_{1}}-5-3i \\  {} {{\text{w}}_{2}}={{z}_{2}}-5-3i \\ \end{array} \right.$ suy ra ${{\text{w}}_{1}}+{{\text{w}}_{2}}={{z}_{1}}+{{z}_{2}}-10-6i=\text{w}-10-6i\Leftrightarrow \left| {{\text{w}}_{1}}+{{\text{w}}_{2}} \right|=\left| \text{w}-10-6i \right|$

Mà $\left\{ \begin{array}  {} \left| {{\text{w}}_{1}} \right|=\left| {{\text{w}}_{2}} \right|=5 \\  {} \left| {{\text{w}}_{1}}-{{\text{w}}_{2}} \right|=\left| {{z}_{1}}-{{z}_{2}} \right|=8 \\ \end{array} \right.$ mà ${{\left| {{\text{w}}_{1}}+{{\text{w}}_{2}} \right|}^{2}}+{{\left| {{\text{w}}_{1}}-{{\text{w}}_{2}} \right|}^{2}}=2\left( {{\left| {{\text{w}}_{1}} \right|}^{2}}+{{\left| {{\text{w}}_{2}} \right|}^{2}} \right)\Rightarrow {{\left| {{\text{w}}_{1}}+{{\text{w}}_{2}} \right|}^{2}}=36.$

Vậy $\left| \text{w}-10-6i \right|=\left| {{\text{w}}_{1}}+{{\text{w}}_{2}} \right|=\sqrt{36}=6\Rightarrow \text{w}$thuộc đường tròn tâm $I\left( 10;6 \right)$, bán kính $R=6$.

Cách 2: Gọi $A\left( {{z}_{1}} \right);B\left( {{z}_{2}} \right)$ biểu diễn số phức${{z}_{1}};{{z}_{2}}$

Ta có: tập hợp $z$ là đường tròn tâm $I\left( 5;3 \right)$ bán kính $R=5,AB=8$

Gọi H là trung điểm của $AB\Rightarrow \text{w}={{z}_{1}}+{{z}_{2}}=+=2\left( 1 \right)$

Mặt khác$IH=\sqrt{I{{A}^{2}}-H{{A}^{2}}}=3\Rightarrow$tập hợp điểm H là đường tròn${{\left( x-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=9\left( C \right)$.

Giả sử $\text{w}\left( a;b \right),\left( 1 \right)\Rightarrow H\left( \frac{a}{2};\frac{b}{2} \right)\in \left( C \right)\Rightarrow {{\left( \frac{a}{2}-5 \right)}^{2}}+{{\left( \frac{b}{2}-3 \right)}^{2}}=9\Leftrightarrow {{\left( a-10 \right)}^{2}}+{{\left( b-6 \right)}^{2}}=36.$

Do đó tập hợp điểm biểu diễn w thuộc đường tròn tâm $I\left( 10;6 \right)$, bán kính $R=6$.

Ta có:${{\left| \text{w} \right|}_{\min }}=\left| OI-R \right|=2\sqrt{34}-6.$ Chọn B.

Ví dụ 9: Cho ${{z}_{1}},{{z}_{2}}$ là hai nghiệm của phương trình $\left| 6-3i+iz \right|=\left| 2z-6-9i \right|$, thỏa mãn điều kiện $\left| {{z}_{1}}-{{z}_{2}} \right|=\frac{8}{5}$. Giá trị lớn nhất của $\left| {{z}_{1}}+{{z}_{2}} \right|$ A. $\frac{31}{5}$ B. $\frac{56}{5}$ C. $4\sqrt{2}$ D. $5$

Lời giải

Đặt $z=x+yi\left( x;y\in \mathbb{R} \right)$ suy ra $\left\{ \begin{array}  {} 6-3i+iz=6-3i+i\left( x+yi \right)=6-y+\left( x-3 \right)i \\  {} 2z-6-9i=2x+2yi-6-9i=2x-6+\left( 2y-9 \right)i \\ \end{array} \right.$

Khi đó, giả thiết$\Leftrightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}={{\left( 2x-6 \right)}^{2}}+{{\left( 2y-9 \right)}^{2}}\Leftrightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=1\,\,\,\,\,\left( C \right)$.

Tập hợp $z$là đường tròn tâm$I\left( 3;4 \right)$bán kính $R=1,AB=\frac{8}{5}$

Đặt $\text{w}={{z}_{1}}+{{z}_{2}}$ gọi H là trung điểm của$AB\Rightarrow \text{w}={{z}_{1}}+{{z}_{2}}=+=2\left( 1 \right)$

Mặt khác$IH=\sqrt{I{{A}^{2}}-H{{A}^{2}}}=\frac{3}{5}\Rightarrow$ tập hợp điểm H là đường tròn ${{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=\frac{9}{25}\,\,\,\left( C \right)$.

Giả sử $\text{w}\left( a;b \right),\left( 1 \right)\Rightarrow H\left( \frac{a}{2};\frac{b}{2} \right)\in \left( C \right)\Rightarrow {{\left( \frac{a}{2}-3 \right)}^{2}}+{{\left( \frac{b}{2}-4 \right)}^{2}}=\frac{9}{25}\Leftrightarrow {{\left( a-6 \right)}^{2}}+{{\left( b-8 \right)}^{2}}=\frac{36}{25}.$

Do đó tập hợp điểm biểu diễn w thuộc đường tròn tâm $I\left( 6;8 \right)$, bán kính $R=\frac{6}{5}$.

Ta có: ${{\left| \text{w} \right|}_{max}}=OI+R=10+\frac{6}{5}=\frac{56}{5}.$

Chọn B.

 

Ví dụ 10: [Đề thi thử chuyên Đại học Vinh 2018] Cho số phức $z$ thỏa mãn $z$ không phải là số thực và $\text{w}=\frac{z}{2+{{z}^{2}}}$ là số thực. Giá trị lớn nhất của biểu thức$M=\left| z+1-i \right|$là A. $2$ B. $2\sqrt{2}$ C. $\sqrt{2}$ D. 8

Lời giải

Ta có $\text{w}=\frac{z}{2+{{z}^{2}}}\Rightarrow \overline{\text{w}}=\overline{\frac{z}{2+{{z}^{2}}}}=\frac{\overline{z}}{2+{{\overline{z}}^{2}}}\left( 1 \right)$. Vì w là số thực nên$\text{w}=\overline{\text{w}}\left( 2 \right)$.

Từ (1), (2)  suy ra $\text{w}=\frac{z}{2+{{z}^{2}}}=\frac{\overline{z}}{2+{{\overline{z}}^{2}}}\Leftrightarrow z\left( 2+{{\overline{z}}^{2}} \right)=\overline{z}\left( 2+{{z}^{2}} \right)\Leftrightarrow 2\left( z-\overline{z} \right)=z.\overline{z}\left( z-\overline{z} \right)$

$\Leftrightarrow \left( z-\overline{z} \right)\left( {{\left| z \right|}^{2}}-2 \right)=0\Leftrightarrow {{\left| z \right|}^{2}}=2\Leftrightarrow \left| z \right|=\sqrt{2}$ (vì $z$không là số thực nên$z-\overline{z}\ne 0$).

Đặt $\text{w}=z+1-i\Leftrightarrow z=\text{w}-1+i$ nên $\left| \text{w}-1+i \right|=\sqrt{2}\Rightarrow {{\left| \text{w} \right|}_{max}}=\sqrt{2}+\sqrt{{{1}^{2}}+{{1}^{2}}}=2\sqrt{2}$. Chọn B.

Cách 2: Ta có w là số thực nên $\frac{1}{\text{w}}=z+\frac{2}{z}$ là số thực.

Đặt $z=a+bi\Rightarrow \frac{1}{\text{w}}=a+bi+\frac{2\left( a-bi \right)}{{{a}^{2}}+{{b}^{2}}}$ là số thực khi $b-\frac{2b}{{{a}^{2}}+{{b}^{2}}}=0\Leftrightarrow \left[ \begin{array}  {} b=0\left( kot/mycbt \right) \\  {} {{a}^{2}}+{{b}^{2}}=2\Rightarrow \left| z \right|=\sqrt{2} \\ \end{array} \right.$

Tập hợp điểm biểu diễn  z  là đường tròn $O\left( 0;0 \right);R=\sqrt{2}$

Đặt $M\left( z \right);A\left( -1;1 \right)\Rightarrow M{{A}_{max}}=AO+R=2\sqrt{2}$. Chọn B.

Ví dụ 11: Cho số phức z thỏa mãn $\left| z \right|=1$. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức$P=\left| z+1 \right|+\left| {{z}^{2}}-z+1 \right|$. Tính giá trị của M.m A. $\frac{13\sqrt{3}}{4}$ B. $\frac{39}{4}$ C. $3\sqrt{3}$               D. $\frac{13}{4}$

Lời giải

Gọi $z=x+yi;\left( x\in \mathbb{R};y\in \mathbb{R} \right)$. Ta có:$\left| z \right|=1\Leftrightarrow z.\overline{z}=1$.

Đặt $t=\left| z+1 \right|,$ta có $0=\left| z \right|-1\le \left| z+1 \right|\le \left| z \right|+1=2\Rightarrow t\in \left[ 0;2 \right]$.

Ta có ${{t}^{2}}=\left( 1+z \right)\left( 1+\overline{z} \right)=1+z.\overline{z}+z+\overline{z}=2+2x\Rightarrow x=\frac{{{t}^{2}}-2}{2}$

Suy ra $\left| {{z}^{2}}-z+1 \right|=\left| {{z}^{2}}-z+z.\overline{z} \right|=\left| z \right|\left| z-1+\overline{z} \right|=\sqrt{{{\left( 2x-1 \right)}^{2}}}=\left| 2x-1 \right|=\left| {{t}^{2}}-3 \right|$

Xét hàm số$f\left( t \right)=t+\left| {{t}^{2}}-3 \right|,t\in \left[ 0;2 \right]$. Bằng cách dùng đạo hàm, suy ra

$\text{max }f\left( t \right)=\frac{13}{4};\min f\left( t \right)=\sqrt{3}\Rightarrow M.n=\frac{13\sqrt{3}}{4}.$

Chọn A.

Ví dụ 12: Cho số phức z  thỏa mãn $\left| z \right|=1$. Tìm giá trị lớn nhất của biểu thức $T=\left| z+1 \right|+2\left| z-1 \right|$ A. $\text{MaxT=2}\sqrt{5}$ B. $\text{MaxT=2}\sqrt{10}$ C. $\text{MaxT=3}\sqrt{5}$              D. $\text{MaxT=3}\sqrt{2}$

Lời giải

$T=\left| z+1 \right|+2\left| z-1 \right|\le \sqrt{\left( 1+{{2}^{2}} \right)\left( {{\left| z+1 \right|}^{2}}+{{\left| z-1 \right|}^{2}} \right)}=\sqrt{5.2\left( {{\left| z \right|}^{2}}+1 \right)}=2\sqrt{5}$(BĐT Cauchy-Swart)

Chú ý: ${{\left| z+1 \right|}^{2}}+{{\left| z-1 \right|}^{2}}=2{{x}^{2}}+2{{y}^{2}}+2=2\left( {{\left| z \right|}^{2}}+1 \right)$ với $z=x+yi$

Cách 2: Đặt $z=x+yi$. Ta có : $T=\left| x+yi+1 \right|+2\left| x-yi-1 \right|=\sqrt{{{(x+1)}^{2}}+{{y}^{2}}}+2\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}$

Lại có ${{x}^{2}}+{{y}^{2}}=1\Rightarrow T=\sqrt{2x+2}+2\sqrt{-2x+2}=f\left( x \right)$

Ta có:$f'\left( x \right)=\frac{1}{\sqrt{2x+2}}-\frac{2}{\sqrt{2-2x}}=0\Leftrightarrow x=\frac{-6}{10}\Rightarrow {{T}_{max}}=2\sqrt{5}$. Chọn A.

Ví dụ 13: Cho số phức z thỏa mãn $\left| z-4 \right|+\left| z+4 \right|=10$. Giá trị lớn nhất và giá trị nhỏ nhất của $\left| z \right|$ lần lượt là : A. 10 và 4 B. 5 và 4 C. 4 và 3 D. 5 và 3

Lời giải

Đặt $z=x+yi;\left( x;y\in \mathbb{R} \right)\Rightarrow M(x;y)$biểu diễn $z$

Ta có: $\left| z-4 \right|+\left| z+4 \right|=10\Leftrightarrow \left| z+yi-4 \right|+\left| x+yi+4 \right|=10$

Gọi ${{F}_{1}}(-4;0);{{F}_{2}}(4;0)\Rightarrow M{{F}_{1}}+M{{F}_{2}}=10$

Khi đó điểm biểu diễn $z$ là Elip có trục lớn

$2a=10\Rightarrow a=5;{{F}_{1}}{{F}_{2}}=2c=8$

$\Rightarrow c=4\Rightarrow b=\sqrt{{{a}^{2}}-{{c}^{2}}}=3$. Do đó $3\le OM\le 5\Rightarrow 3\le \left| z \right|\le 5$. Chọn D.