Bài tập Hình nón nội - ngoại tiếp hình trụ, hình cầu

Bài tập Hình nón nội - ngoại tiếp hình trụ, hình cầu
Hình nón ngoại tiếp hình cầu
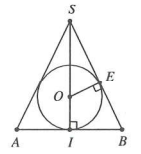
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác ngoại tiếp đường tròn
Bài toán: Gọi R, r, h lần lượt là bán kính mặt cầu, bán kính đáy và chiều cao hình nón $\Rightarrow R=OI,r=IB,h=SI$
Ta có $\Delta SEO\sim\Delta SIB\Rightarrow \frac{OE}{IB}=\frac{SO}{SB}\Rightarrow \frac{R}{r}=\frac{h-R}{\sqrt{{{h}^{2}}+{{r}^{2}}}}$
Vậy mối liên hệ cần tìm là $$
Hình nón nội tiếp hình cầu
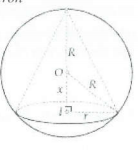
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác nội tiếp đường tròn
Bài toán: Gọi R, r, h lần lượt là bán kính mặt cầu, bán kính đáy và chiều cao hình nón
Ta có ${{x}^{2}}+{{r}^{2}}={{R}^{2}}$ mà $x=h-R\Rightarrow {{\left( h-R \right)}^{2}}+{{r}^{2}}={{R}^{2}}$
Vậy mối liên hệ cần tìm là $$
Hình nón ngoại tiếp hình trụ

Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác ngoại tiếp hình chữ nhật, cụ thể là tam giác SAB (thiết diện qua trục hình nón) và hình chữ nhật MNPO (thiết diện qua trục hình trụ)
Bài toán: Gọi R, h, R’, H’ lần lượt là bán kính đáy và chiều cao hình nón; bán kính đáy và chiều cao hình trụ $\Rightarrow \left\{ \begin{array} {} R=IA \\ {} h=SI \\ \end{array} \right.;\left\{ \begin{array} {} R'=IN \\ {} h=OI \\ \end{array} \right.$
Ta có $\Delta AMN\sim\Delta ASI\Rightarrow \frac{MN}{SI}=\frac{AN}{AI}\Rightarrow \frac{h'}{h}=\frac{R-R'}{R}$
Vậy mối liên hệ cần tìm là $$
| Bài tập 1: Cho hình cầu bán kính bằng 5 cm, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo thành là một đường tròn đường kính 4 cm. Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm của hình cầu đã cho.
A. $\approx 19,18c{{m}^{3}}$ B. $\approx 19,20c{{m}^{3}}$ C. $\approx 19,21c{{m}^{3}}$ D. $\approx 19,19c{{m}^{3}}$ |
Lời giải chi tiết
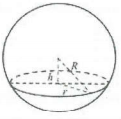
Theo bài ra, ta có R = 5 cm, r = 2 cm
Chiều cao của khối nón là $h=\sqrt{{{R}^{2}}-{{r}^{2}}}=\sqrt{21}cm$
Vậy thể tích khối nón là $V=\frac{1}{3}\pi {{r}^{2}}h=\frac{4\sqrt{21}\pi }{3}\approx 19,20c{{m}^{3}}$.
Chọn B.
| Bài tập 2: Cho mặt cầu (S) tâm O, bán kính R (không đổi). Mặt phẳng (P) cách O một khoảng bằng x, (x< R) và cắt (S) theo giao tuyến là đường tròn (C) có tâm H. Gọi T là giao điểm của tia HO với (S). Thể tích của khối nón có đỉnh T và đáy là hình tròn (C) bằng
A. $\frac{\pi \left( {{R}^{2}}-{{x}^{2}} \right)\left( R+h \right)}{6}$ B. $2\pi \left( {{R}^{2}}-{{x}^{2}} \right)\left( R+h \right)$ C. $\frac{\pi \left( {{R}^{2}}-{{x}^{2}} \right)\left( R+h \right)}{3}$ D. $\pi \left( {{R}^{2}}-{{x}^{2}} \right)\left( R+h \right)$ |
Lời giải chi tiết
Bán kính đáy hình nón là $r=\sqrt{{{R}^{2}}-{{x}^{2}}}$
Chiều cao hình nón là $h=OT+OH=R+h$
Vậy thể tích khối nón là $V=\frac{1}{3}\pi {{r}^{2}}h=\frac{\pi \left( {{R}^{2}}-{{x}^{2}} \right)\left( R+h \right)}{3}$
Chọn C.
| Bài tập 3: Cho hình nón (N) có bán kính đáy bằng 6, chiều cao bằng 8. Biết rằng có một mặt cầu tiếp xúc với tất cả các đường sinh của hình nón, đồng thời tiếp xúc với mặt đáy của hình nón. Tìm bán kính của mặt cầu đó
A. 4 B. 2 C. 6 D. 3 |
Lời giải chi tiết
Bài toán: Hình nón ngoại tiếp hình cầu $\Rightarrow R=\frac{rh}{r+\sqrt{{{r}^{2}}+{{h}^{2}}}}=\frac{6.8}{6+\sqrt{{{6}^{2}}+{{8}^{2}}}}=3$
Chọn D.
| Bài tập 4: Cho khối cầu tâm O, bán kính R =2. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón (N) có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón (N) có thể tích lớn nhất, khi đó giá trị của x bằng
A. $x=\frac{2}{3}$ B. $x=\frac{\sqrt{3}}{3}$ C. $x=\frac{1}{3}$ D. $x=\frac{\sqrt{3}}{2}$ |
Lời giải chi tiết
Bài toán: Hình nón nội tiếp hình cầu.
Ta có ${{r}^{2}}={{R}^{2}}-{{x}^{2}}$, với r là bán kính đáy hình nón
Chiều cao hình nón là $h=x+R$. Thể tích khối nón là $V=\frac{1}{3}\pi {{r}^{2}}h=\frac{1}{3}\pi \left( {{R}^{2}}-{{x}^{2}} \right).\left( x+R \right)$
Lại có $V=\frac{\pi }{6}.\left( 2R-2x \right).\left( R+x \right).\left( R+x \right)\le \frac{\pi }{6}.\frac{{{\left( 2R-2x+R+x+R+x \right)}^{3}}}{27}=\frac{32\pi {{R}^{3}}}{81}$
Dấu bằng xảy ra khi và chỉ khi $2R-2x=R+x\Leftrightarrow x=\frac{R}{3}=\frac{2}{3}$
Chọn A.
| Bài tập 5: Cho hình nón tròn xoay (N) có đỉnh là S, có đáy là đường tròn tâm O bán kính R. Đường cao SO = h. Tính chiều cao x của hình trụ có thể tích lớn nhất nội tiếp hình nón đã cho ?
A. $x=\frac{h}{3}$ B. $x=\frac{h\sqrt{3}}{3}$ C. $x=\frac{h}{6}$ D.$x=\frac{h\sqrt{3}}{6}$ |
Lời giải chi tiết
Bài toán: Hình nón ngoại tiếp hình trụ $\Rightarrow \frac{h'}{h}=\frac{R-R'}{R}$
Với R’, h’ lần lượt là bán kính đáy, chiều cao hình trụ $\Rightarrow x=\frac{h}{R}.\left( R-R' \right)$
Thể tích khối trụ là $V=\pi R{{'}^{2}}x=\pi R{{'}^{2}}.\frac{h}{R}.\left( R-R' \right)=\frac{\pi h}{R}.\left[ R{{'}^{2}}.(R-R') \right]$
Ta có: $R{{'}^{2}}.\left( R-R' \right)=4.\frac{R'}{2}.\frac{R'}{2}.(R-R')\le 4.\frac{{{\left( \frac{R'}{2}+\frac{R'}{2}+R-R' \right)}^{3}}}{27}=\frac{4{{R}^{3}}}{27}$
Suy ra $V\le \frac{\pi h}{R}.\frac{4{{R}^{3}}}{27}=\frac{4\pi {{R}^{2}}h}{27}$. Dấu = xảy ra khi $\frac{R'}{2}=R-R'\Rightarrow R'=\frac{2}{3}R\Rightarrow x=\frac{h}{3}$.
Chọn A.
TOÁN LỚP 12
