Bài tập mặt cầu khối cầu mức độ nhận biết thông hiểu có đáp án chi tiết

Bài tập mặt cầu khối cầu mức độ nhận biết thông hiểu có đáp án chi tiết

Dưới đây làm một số bài toán về mặt cầu, khối cầu hay ra trong đề thi đại học, thpt quốc gia

Lời giải chi tiết

Diện tích xung quanh hình lập phương cạnh a là ${{S}_{xq}}=4{{a}^{2}}\xrightarrow{{}}{{S}_{mc}}=4{{a}^{2}}$

Suy ra bán kính mặt cầu là $4\pi {{R}^{2}}=4{{a}^{2}}\Leftrightarrow {{R}^{2}}=\frac{{{a}^{2}}}{\pi }\Rightarrow R=\frac{a}{\sqrt{\pi }}$

Vậy thể tích khối cầu cần tính là $V=\frac{4}{3}\pi {{R}^{2}}=\frac{4{{a}^{3}}}{3\sqrt{\pi }}.$ Chọn D.

Lời giải chi tiết

Hình vẽ tham khảo

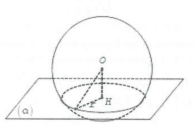
Gọi H là hình chiếu của O xuống mp$\left( \alpha  \right)$. Ta có $d\left( O;\left( \alpha  \right) \right)=OH=\frac{R}{2}<R$ nên $\left( \alpha  \right)$ cắt $S\left( O;R \right)$ theo đường tròn $C\left( H;r \right)$. Bán kính đường tròn $C\left( H;r \right)$ là $r=\sqrt{{{R}^{2}}-O{{H}^{2}}}=\frac{R\sqrt{3}}{2}.$

Suy ra dường kính của đường tròn cần tính bằng $\frac{R\sqrt{3}}{2}.$ Chọn B.

Lời giải chi tiết

Gọi H là hình chiếu của O lên BC.

Ta có $OB=OC=R,$ suy ra H là trung điểm của BC nên $HC=\frac{CD}{2}=\frac{R\sqrt{3}}{2}.$

Suy ra $OH=\sqrt{O{{C}^{2}}-H{{C}^{2}}}=\frac{R}{2}.$ Chọn B.

Lời giải chi tiết

Theo giả thiết, ta có $AH=\frac{8}{3}.$ Ta suy ra $OH=AH-OA=\frac{2}{3}.$

Gọi $r'$ là bán kính của đường tròn $\left( C \right)$. Ta có $r{{'}^{2}}={{r}^{2}}-O{{H}^{2}}={{2}^{2}}-{{\left( \frac{2}{3} \right)}^{2}}=\frac{32}{9}.$

Vậy diện tích cùa đường tròn$\left( C \right)$ là $S=\pi r{{'}^{2}}=\frac{32\pi }{9}.$ Chọn A.

Lời giải chi tiết

Gọi khoảng cách từ tâm cầu đến mặt phẳng là d, ta có ${{d}^{2}}={{R}^{2}}-{{r}^{2}}.$

Hình tròn lớn của hình cầu S là hình tròn tạo bởi mặt phẳng cắt hình cầu và đi qua tâm của hình cầu.

Gọi R là bán kính hình cầu thì hình tròn lớn cũng có bán kính là R .

Theo giả thiết, ta có $\pi {{R}^{2}}=4\pi \Leftrightarrow R=2$và $\pi {{r}^{2}}=2\pi \Leftrightarrow r=\sqrt{2}$.

Suy ra $d=\sqrt{{{R}^{2}}-{{r}^{2}}}=\sqrt{{{2}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}=\sqrt{2}.$ Chọn D.

Lời giải chi tiết

Hình vẽ tham khảo

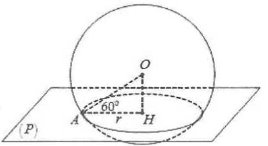
Gọi H là hình chiếu vuông góc của O trên $\left( P \right)$ thì

H là tâm của đường tròn giao tuyến của $\left( P \right)$ và $\left( S \right)$.

$\widehat{\left( OA;\left( P \right) \right)}=\widehat{\left( OA;AH \right)}={{60}^{0}}.$ 

Bán kính của đường tròn giao tuyến $r=HA=OA.cos{{60}^{0}}=\frac{R}{2}.$

Suy ra diện tích dường tròn giao tuyến $\pi {{r}^{2}}=\pi {{\left( \frac{R}{2} \right)}^{2}}=\frac{\pi {{R}^{2}}}{4}.$ Chọn C.

Lời giải chi tiết

Đặt $OA=OB=x.$ Tam giác OAB là tam giác đều

${{S}_{\Delta OAB}}=\frac{{{x}^{2}}\sqrt{3}}{4}.$ Mặt phẳng $\left( OAB \right)$ là hình chiếu của mặt phẳng $\left( IAB \right)$ trên mặt phẳng $\left( P \right)$.

${{S}_{\Delta OAB}}={{S}_{\Delta IAB}}.cos\varphi$ với $\varphi =\widehat{\left( IAB \right);\left( OAB \right)}={{60}^{0}}$.

${{S}_{\Delta OAB}}=\frac{{{S}_{\Delta IAB}}}{2}=\frac{\sqrt{3}}{4}\Rightarrow \frac{{{x}^{2}}\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\Leftrightarrow x=1.$

Gọi M là trung điểm của AB $\Rightarrow \widehat{IMO}={{60}^{0}}\Rightarrow IO=\frac{3}{2}.$ 

Vậy $R=IA=\sqrt{I{{O}^{2}}+A{{O}^{2}}}=\sqrt{{{\left( \frac{3}{2} \right)}^{2}}+{{1}^{2}}}=\frac{\sqrt{13}}{2}.$ Chọn C.

Lời giải chi tiết

Gọi $a,b,c$ lần lượt là khoảng cách từ I đến mặt phẳng $\left( P \right),\left( Q \right),\left( R \right)$.

Gọi ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ lần lượt là bán kính đường tròn giao tuyến của mặt cầu $\left( S \right)$ với $\left( P \right),\left( Q \right),\left( R \right)$.

Khi đó ${{R}^{2}}={{a}^{2}}+r_{1}^{2};{{R}^{2}}={{b}^{2}}+r_{2}^{2};{{R}^{2}}={{c}^{2}}+r_{3}^{2}\Rightarrow 3{{R}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+\left( r_{1}^{2}+r_{2}^{2}+r_{3}^{2} \right)\text{       (*)}\text{.}$

Mà ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=I{{A}^{2}};{{S}_{1}}+{{S}_{2}}+{{S}_{3}}=\pi \left( r_{1}^{2}+r_{2}^{2}+r_{3}^{2} \right).$

Suy ra (*)$\Leftrightarrow 3{{R}^{2}}=I{{A}^{2}}+\frac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}}{\pi }=3+12=15\Rightarrow R=\sqrt{5}.$ Chọn B.