Mầu nguyên tử bohr là gì? Lý thuyết tóm tắt ngắn gọn

LÝ THUYẾT TRỌNG TÂM

1. Các tiên đề Bohr

Tiên đề 1: Trạng thái dừng của nguyên tử.

"Nguyên tử chỉ tồn tại ở trạng thái có năng lượng xác định gọi là trạng thái dừng. Khi ở trạng thái dừng, nguyên tử không bức xạ.

Trong các trạng thái dừng của nguyên tử, các electron sẽ chuyển động trên những quỹ đạo có bán kính xác định gọi là quỹ đạo dừng."

Tiên đề 2: Sự bức xạ và hấp thụ năng lượng của nguyên tử.

"Khi chuyển từ trạng thái dừng có năng lượng ${{E}_{n}}$sang trạng thái dừng có năng lượng thấp ${{E}_{m}}$, nguyên tử sẽ bức xạ một phôtôn có năng lượng $\varepsilon ={{E}_{n}}-{{E}_{m}}$.

Ngược lại khi nguyên tử đang ở trạng thái dừng có năng lượng ${{E}_{m}}$, hấp thụ một phôtôn có năng

lượng $\varepsilon ={{E}_{n}}-{{E}_{m}}$thì nó sẽ chuyển lên trạng thái có năng lượng cao ${{E}_{n}}$."

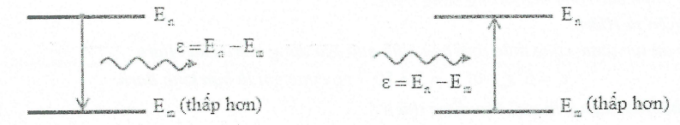
- Năng lượng ion hóa là năng lượng tối thiểu để tách một electron từ nguyên tử ở trạng thái cơ bản.

2. Sự tạo thành quang phổ vạch nguyên tử Hidro.

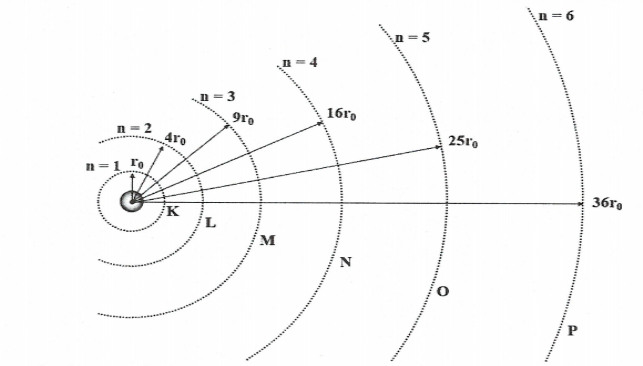
a) Quỹ đạo dừng của nguyên tử Hidro.

Nguyên tử Hidro có một electron, mỗi trạng thái dừng của nguyên tử H ứng với một quỹ đạo dừng của electron.

- Chứng minh các công thức trong bảng trên:

Xét nguyên tử Hidro:

+) Bohr đã tìm được công thức tính bán kính quỹ đạo dừng thứ n của Hidro:

${{\lambda }_{32}}=0,6563\mu m$ với ${{r}_{0}}=5,{{3.10}^{-11}}\,m$ được gọi là bán kính Bohr.

+) Lực hút tĩnh điện trên quỹ đạo dừng thứ n :

${{F}_{n}}=k\frac{{{e}^{2}}}{r_{{}}^{2}}=k\frac{{{e}^{2}}}{{{n}^{4}}.r_{0}^{2}}\Rightarrow {{F}_{n}}=\frac{{{F}_{0}}}{n}$với ${{F}_{0}}=k\frac{{{e}^{2}}}{r_{0}^{2}}$là lực hút tĩnh điện trên quỹ đạo cơ bản (n = 1).

+) Lực tĩnh điện giữa electron và hạt nhân đóng vai trò là lực hướng tâm, làm electron chuyển động tròn quanh hại nhân:${{F}_{n}}={{F}_{ht}}\Leftrightarrow k\frac{{{e}^{2}}}{r_{{}}^{2}}=m\frac{{{v}^{2}}}{r}(k={{9.10}^{9}}\,N{{m}^{2}}/{{C}^{2}}:$ hằng số điện môi).

$\Rightarrow v=\sqrt{\frac{k{{e}^{2}}}{mr}}=\sqrt{\frac{k{{e}^{2}}}{m.{{n}^{2}}.{{r}_{0}}}}=\frac{1}{n}\sqrt{\frac{k{{e}^{2}}}{m{{r}_{0}}}}$

Vận tốc của electron ở quỹ đạo cơ bản n = 1 (mức K) là ${{v}_{0}}=\sqrt{\frac{k{{e}^{2}}}{m{{r}_{0}}}}$

$\Rightarrow $Vận tốc của electron ở quỹ đạo dừng thứ n là ${{v}_{n}}=\frac{{{v}_{0}}}{n}$

+) Thế năng tương tác tĩnh điện giữa electron và hạt nhân: ${{\text{W}}_{t}}=-\frac{k{{e}^{2}}}{r}.$

Động năng của electron: ${{\text{W}}_{d}}=\frac{m{{v}^{2}}}{2}=\frac{k{{e}^{2}}}{2r}$

Năng lượng toàn phần: $E={{\text{W}}_{t}}+{{\text{W}}_{d}}=-\frac{k{{e}^{2}}}{2r}\,\,\,\left( * \right)$

Năng lượng của electron trên quỹ đạo dừng thứ n: $E=-k\frac{{{e}^{2}}}{2r}=-k\frac{{{e}^{2}}}{2{{n}^{2}}{{r}_{0}}}\Rightarrow {{E}_{n}}=\frac{-{{E}_{0}}}{{{n}^{2}}}$.

Với ${{E}_{0}}=k\frac{{{e}^{2}}}{2{{r}_{0}}}={{9.10}^{9}}.\frac{{{(1,{{6.10}^{-19}})}^{2}}}{2.5,{{3.10}^{-11}}}=2,{{17.10}^{-18}}\,J=13,6\,eV$: năng lượng ion hóa của Hydro.

b) Đặc điểm cấu trúc thang năng lượng của Hidro.

- Các mức năng lượng càng lên cao càng sít nhau hay $\Delta E$ càng giảm: $\Delta {{E}_{21}}>\Delta {{E}_{32}}>...$

- Không có khe năng lượng nào giống khe năng lượng nảo.

Khe năng lượng ở mức n và n-1 là:

$\Delta E={{E}_{n}}-{{E}_{n-1}}=\left( -\frac{{{E}_{0}}}{{{n}^{2}}} \right)-\left( -\frac{{{E}_{0}}}{{{(n-1)}^{2}}} \right)={{E}_{0}}\left( \frac{1}{{{(n-1)}^{2}}}-\frac{1}{{{n}^{2}}} \right)$

- Chú ý:

+) Mỗi trạng thái dừng của nguyên tử tương ứng với một tập hợp các quỹ đạo dừng của electron.

+) Năng lượng của nguyên tử = tổng động năng + tổng thế năng tương tác.

+) Trạng thái cơ bản là trạng thái có năng lượng thấp nhất (bền vững nhất), electron lấp đầy mức thấp rồi lên mức cao. Trạng thái cơ bản của Hidro là khi electron ở mức K (n = 1).

+) Khi bị kích thích electron nhảy lên mức trên có năng lượng cao (trạng thái kích thích) không bền và nó chỉ tồn tại 10^-8 s sau tự nhảy về mức thấp và bức xạ ra phôtôn.

c) Số loại phôtôn bức xạ (số vạch phổ).

• - Khi kích thích từ mức cơ bản: Có bao nhiêu cách dịch chuyển xuống của electron thì sẽ có bấy nhiêu loại phôtôn được phát ra.

+) Nếu chỉ có một nguyên tử Hidro đang ở trạng thái kích thích ${{E}_{n}}$sau đó nó bức xạ tối đa (n - 1)

phôtôn.

+) Nếu khối khí Hidro đang ở trạng thái kích thích ${{E}_{n}}$sau đó nó bức xạ tối đa là $\frac{n(n-1)}{2}$ vạch quang phổ. - Trong các vạch bức xạ phát ra, vạch có:

+) Bước sóng ngắn nhất (tần số lớn nhất) ứng với khe năng lượng lớn nhất:

$\frac{hc}{{{\lambda }_{\min }}}=h{{f}_{\max }}={{\varepsilon }_{\max }}={{E}_{n}}-{{E}_{1}}={{E}_{0}}\left( 1-\frac{1}{{{n}^{2}}} \right)$

+) Bước sóng dài nhất (tần số nhỏ nhất) ứng với khe năng lượng nhỏ nhất. Do khoảng cách giữa 2 mức năng lượng càng lên cao càng dày nên 2 mức kích thích trên cùng n và n-l có khe năng lượng nhỏ nhất:

$\frac{hc}{{{\lambda }_{\text{max}}}}=h{{f}_{\min }}={{\varepsilon }_{\min }}={{E}_{n}}-{{E}_{n-1}}={{E}_{0}}\left( \frac{1}{{{(n-1)}^{2}}}-\frac{1}{{{n}^{2}}} \right)$

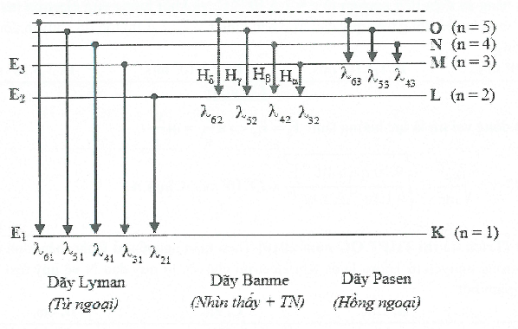
d) Các dãy quang phổ vạch phát xạ của Hidro.

Các vạch quang phổ thu được của Hidro được chia thành 3 dãy:

▪ Dãy Lyman: Gồm các vạch phát ra khi electron chuyển từ trạng thái có mức năng lượng cao hơn về mức K (quan sát được nhờ chất phát quang).

Bước sóng càng ngắn năng lượng càng lớn nên:

+) Vạch ngắn nhất ${{\lambda }_{L\min }}={{\lambda }_{\infty L}}({{f}_{L\max }})$khi electron chuyển từ $\infty $ về K:

$\frac{1}{{{\lambda }_{L\min }}}=\frac{1}{{{\lambda }_{\infty L}}}=\frac{{{E}_{0}}}{hc}\Rightarrow $

+) Vạch dài nhất ${{\lambda }_{Lm\text{ax}}}={{\lambda }_{21}}({{f}_{L\min }})$ khi electron chuyển từ L về K:

$\frac{1}{{{\lambda }_{L\min }}}=\frac{1}{{{\lambda }_{21}}}=\frac{{{E}_{0}}}{hc}\left( \frac{1}{{{1}^{2}}}-\frac{1}{{{2}^{2}}} \right)=\frac{3{{E}_{0}}}{4c}\Rightarrow {{\lambda }_{L\min }}=\frac{4hc}{3{{E}_{0}}}=\frac{4}{3}{{\lambda }_{L\min }}=121,8\,nm$

$\Rightarrow $ Toàn bộ dãy Lyman nằm trong vùng tử ngoại có ${{\lambda }_{n1}}\in \left[ 91,3\,nm;\,\,121,8\,nm \right]:$

$\begin{array}{} {{\varepsilon }_{n1}}=\frac{hc}{{{\lambda }_{n1}}}={{E}_{0}}\left( 1-\frac{1}{{{n}^{2}}} \right)\Rightarrow \frac{1}{{{\lambda }_{n1}}}=\frac{{{E}_{0}}}{hc}\left( 1-\frac{1}{{{n}^{2}}} \right)=\frac{1}{{{\lambda }_{L\min }}}\left( 1-\frac{1}{{{n}^{2}}} \right) \\ {} \\ \end{array}$với n ≥ 2.

▪ Dãy Banme: Gồm các vạch phát ra khi các electron từ trạng thái có mức năng lượng cao về L (n về 2):

${{\varepsilon }_{n2}}=h{{f}_{n2}}=\frac{hc}{{{\lambda }_{n2}}}={{E}_{n}}-{{E}_{2}}={{E}_{0}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{n}^{2}}} \right)\Rightarrow \frac{1}{{{\lambda }_{n2}}}=\frac{hc}{{{E}_{0}}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{n}^{2}}} \right)=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{4}-\frac{1}{{{n}^{2}}} \right)$với n ≥ 3.

+) Vạch ngắn nhất ${{\lambda }_{B\min }}={{\lambda }_{\infty 2}}$: khi electron từ $\infty $ về L:

$\frac{1}{{{\lambda }_{B\min }}}=\frac{1}{{{\lambda }_{\infty 2}}}=\frac{1}{4{{\lambda }_{L\min }}}\Rightarrow {{\lambda }_{B\min }}={{\lambda }_{\infty 2}}=4{{\lambda }_{L\min }}=365,2\,nm.$

+) Vạch dài nhất ${{\lambda }_{B\max }}={{\lambda }_{32}}$: khi electron từ M về L:

$\frac{1}{{{\lambda }_{B\max }}}=\frac{1}{{{\lambda }_{32}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{4}-\frac{1}{9} \right)\Rightarrow {{\lambda }_{B\min

}}={{\lambda }_{32}}=\frac{36}{5}{{\lambda }_{L\min }}=657,4\,nm$: màu đỏ (${{H}_{\alpha }}$)

Và các vạch:

$\frac{1}{{{\lambda }_{42}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{4}-\frac{1}{{{4}^{2}}} \right)\Rightarrow {{\lambda }_{42}}=\frac{16}{3}{{\lambda }_{L\min }}=485\,nm$: màu lam (H_β)

$\frac{1}{{{\lambda }_{52}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{5}^{2}}} \right)\Rightarrow {{\lambda }_{52}}=\frac{100}{21}{{\lambda }_{L\min }}=433\,nm$: màu chàm (H_γ)

$\frac{1}{{{\lambda }_{62}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{6}^{2}}} \right)\Rightarrow {{\lambda }_{62}}=\frac{9}{2}{{\lambda }_{L\min }}=409\,nm$: màu tím (H_δ)

…

$\Rightarrow $ Dãy Banme gồm 4 vạch trong vùng nhìn thấy là đỏ (H_α), lam (H_β), chàm (H_γ), tím (H_δ) và một số vạch thuộc vùng tử ngoại.

▪ Dãy Pasen: Gồm các vạch phát ra khi electron chuyển từ trạng thái có mức năng lượng cao về mức M (n về 3):

${{\varepsilon }_{n3}}=h{{f}_{n3}}=\frac{hc}{{{\lambda }_{n3}}}={{E}_{0}}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{n}^{2}}} \right)\Rightarrow \frac{1}{{{\lambda }_{n3}}}=\frac{{{E}_{0}}}{hc}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{n}^{2}}} \right)=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{n}^{2}}} \right)$ với n ≥ 3.

+) Vạch ngắn nhất ${{\lambda }_{P\min }}={{\lambda }_{\begin{smallmatrix} \infty 3 \\

\end{smallmatrix}}}$: khi từ $\infty $về M:

$\frac{1}{{{\lambda }_{\infty 3}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{\infty }^{2}}} \right)\Rightarrow {{\lambda }_{\infty 3}}=9{{\lambda }_{L\min }}=819\,nm$

+) Vạch dài nhất ${{\lambda }_{P\max }}={{\lambda }_{\begin{smallmatrix} 43 \\

\end{smallmatrix}}}$: khi từ N về M:

$\frac{1}{{{\lambda }_{43}}}=\frac{1}{{{\lambda }_{L\min }}}\left( \frac{1}{{{3}^{2}}}-\frac{1}{{{4}^{2}}} \right)\Rightarrow {{\lambda }_{\infty 3}}=\frac{144}{7}{{\lambda }_{L\min }}=1872\,nm$

$\Rightarrow $Dãy Pasen nằm trọn vẹn trong vùng hồng ngoại.

Sơ đồ chuyển mức năng lượng của nguyên tử Hidro khi tạo thành dãy quang phổ.