Bài tập sóng âm có đáp án chi tiết

BÀI TẬP SÓNG ÂM CÓ ĐÁP ÁN CHI TIẾT

Dạng 1: Các câu hỏi lí thuyết về Sóng âm

Bài tập 1: Một sóng âm truyền từ không khí vào nước thì: A. Tần số và bước sóng đều thay đổi. B. Tần số không thay đổi, còn bước sóng thay đổi. C. Tần số thay đổi, còn bước sóng không thay đổi. D. Tần số và bước sóng đều không thay đổi.

Lời giải chi tiết:

Sóng âm truyền qua các môi trường thì tần số song không thay đổi.

Vận tốc song thay đổi nên bước sóng $\lambda =\frac{\text{v}}{\text{f}}$  thay đổi. Chọn B.

Bài tập 2: Khi nói về sóng âm, phát biểu nào sau đây là sai? A. Sóng cơ có tần số nhỏ hơn 16Hz gọi là sóng hạ âm. B. Sóng hạ âm không truyền được trong chân không. C. Sóng cơ có tần số lớn hơn 20000Hz gọi là sóng siêu âm. D. Sóng siêu âm truyền được trong chân không.

Lời giải chi tiết

Sóng âm không truyền được trong chân không. Chọn D.

 

Bài tập 3: Điều nào sau đây là sai khi nói về sóng âm? A. Sóng âm là sóng cơ học truyền trong các môi trường vật chất như rắn, lỏng, khí. B. Sóng âm là sóng cơ học dọc. C. Sóng âm không truyền được trong chân không. D. Vận tốc truyền âm trong cùng một môi trường thì phụ thuộc vào nhiệt độ.

Lời giải chi tiết

Sóng âm có thể là sóng ngang, hoặc sóng đọc, tuỳ thuộc vào môi trường sóng truyền qua. Chọn B.

Bài tập 4: Chọn câu sai trong các câu sau. Sóng âm: A. không truyền được trong chân không. B. truyền được trong cả 3 môi trường rắn, lỏng, khí. C. Có vận tốc truyền phụ thuộc nhiệt độ. D. Chỉ có sóng âm có tần số trong khoảng từ 16Hz đến 2000Hz mới truyền được trong không khí.

Lời giải chi tiết:

Sóng âm có thể truyền được trong cả ba môi trường rắn lỏng khí và không truyền được trong chân không. Chọn D.

Bài tập 5: Hãy chọn kết luận đúng : A. Sóng âm không truyền được trong nước . B. Cường độ âm là năng lượng được sóng âm truyền qua 1 đơn vị diện tích trong 1 đơn vị thời gian. C. Vận tốc truyền âm phụ thuộc vào nhiệt độ của môi trường. D. Sóng âm truyền được trong chân không .

Lời giải chi tiết

Vận tôc truyền âm phụ thuộc vào nhiệt độ của môi trường.

Cường độ âm I tại một điểm là đại lượng đo bằng năng lượng mà sóng âm tải qua đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian. Chọn C.

Bài tập 6: Độ cao của âm phụ thuộc yếu tố nào của nguồn âm.? A. Pha dao động B. Tần số C. Biên độ dao động D. Tất cả các yếu tố trên.

Lời giải chi tiết:

Độ cao của âm phụ thuộc vào tần số.. Chọn B.

Bài tập 7: Tai ta cảm nhận được âm thanh khác biệt của các nốt nhạc Đô, Rê, Mi, Fa, Sol, La, Si khi chúng phát ra từ một nhạc cụ nhất định là do các âm thanh này khác nhau : A. biên độ âm. B. cường độ âm. C. tần số âm. D. âm sắc.

Lời giải chi tiết:

Do các âm thanh này khác nhau về tần số âm. Chọn C.

Bài tập 8: Âm sắc là đặc tính sinh lí của âm phụ thuộc vào A. chỉ tần số       B. chỉ biên độ. C. biên độ và tần số.      D. chỉ cường độ âm.

Lời giải chi tiết:

Âm sắc liên quan mật thiệt đến đồ thị dao động âm nó phụ thuộc vào biên độ và tần số âm Chọn C.

Bài tập 9: Hai âm có cùng độ cao, chúng có cùng đặc điểm nào trong các đặc điểm sau ? A. Cùng tần số.      B. Cùng biên độ. C. Cùng bước sóng trong một môi trường.   D. Cả đáp án A và C

Lời giải chi tiết:

Hai âm có cùng độ cao thì có cùng tần số.

Mặt khác $\lambda =\frac{\text{v}}{\text{f}}$nên trong cùng môi trường nó có cùng bước sóng. Chọn D.

Bài tập 10: Cường độ âm là năng lượng âm: A. Truyền qua một đơn vị diện tích đặt vuông góc phương truyền âm, đơn vị là W / m2. B. Truyền trong một đơn vị thời gian, đơn vị là W / m2. C. truyền trong một đơn vị thời gian qua một đơn vị diện tích đặt vuông góc với phương truyền âm, đơn vị là W / m2. D. truyền trong một đơn vị thời gian qua một đơn vị diện tích đặt vuông góc với phương truyền âm, đơn vị là J / s.

Lời giải chi tiết:

Cường độ âm là năng lượng âm truyền trong một đơn vị thời gian qua một đơn vị diện tích đặt vuông góc với phương truyền âm, đơn vị là W / m² . Chọn A.

Bài tập 11: Trong quá trình truyền sóng âm trong không gian đẳng hướng từ một nguồn điểm và không có sự hấp thụ âm, năng lượng sóng truyền tới một điểm sẽ: A. giảm tỉ lệ với khoảng cách đến nguồn B. giảm tỉ lệ với bình phương khoảng cách đến nguồn C. giảm tỉ lệ với lập phương khoảng cách đến nguồn D. không đổi

Lời giải chi tiết:

Năng lượng sóng truyền tới một điểm sẽ giảm tỉ lệ với bình phương khoảng cách đến nguồn. Chọn B.

Bài tập 12: [ Trích đề thi chuyên Hạ Long – Quảng Ninh]. Âm do một chiếc đàn bầu phát ra A. Có âm sắc phụ thuộc vào dạng đồ thị dao động của âm. B. Nghe càng cao khi biên độ âm càng lớn. C. Có độ cao phụ thuộc vào hình dạng và kích thước hộp cộng hưởng. D. Nghe càng trầm khi tần số âm càng lớn.

Lời giải chi tiết:

Âm sắc phụ thuộc vào dạng đồ thị dao động của âm. Chọn A.

Dạng 2: Xác định các đại lượng đặc trưng của sóng âm (Tần số, bước sóng, vận tốc).

PHƯƠNG PHÁP GIẢI

- Bước 1: Tóm tắt đề: Đề cho gì?, hỏi gì? Và đổi các đơn vị sang các đơn vị hợp pháp

- Bước 2: Xác lập mối quan hệ giữa các đại lượng cho và đại lượng tìm thông qua các công thức:

- Cộng hưởng âm:

Hai đầu là nút sóng khi cộng hưởng âm : $\ell =\text{k}\frac{\lambda }{2}(\text{k}\in {{\mathbb{N}}^{*}})$

Số bụng sóng = số bó sóng = k. Số nút sáng = k+1

Một đầu là nút sóng còn một đầu là bụng sóng: $\ell =(\text{k+0,5)}\frac{\lambda }{2}(\text{k}\in \mathbb{N})$

Số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k+1

Tốc độ truyền sóng: $\text{v = f}\lambda \text{ =}\frac{\lambda }{\text{T}}$

- Bước 3: Suy ra biểu thức xác định đại lượng tìm theo các đại lượng cho và các dữ kiện.

- Bước 4: Thực hiện tính toán để xác định giá trị đại lượng tìm và lựa chọn câu trả lời đúng.

BÀI TẬP MINH HỌA DẠNG 2

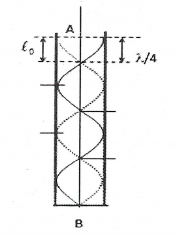
Bài tập 1: Một ống sáo dài 75 cm, một đầu bịt kín một đầu hở, biết vận tốc truyền âm trong không khí là 340 m/s. Xác định tần số lớn nhất mà ống sáo phát ra mà một người bình thường có thể nghe được? (Kết quả gần đúng đến 2 số sau dấu phẩy). A. 19,72 kHz. B. 19,94 kHz C. 20,06 kHz. D. 19,83 kHz

HD giải:

Trong ống sáo có một đầu bịt kín và một đầu để hở. Ta có: $\ell =(\text{k + 0,5)}\frac{\lambda }{2}=(\text{k + 0,5)}\frac{\text{v}}{2\text{f}}\Rightarrow \text{f =}\frac{(\text{k + 0,5) v}}{2\ell }$ Để người bình thường có thể nghe được : f ≤ 20000 Hz $\Rightarrow (\text{k + 0,5)}\frac{\text{v}}{2\ell }\le 20000\Rightarrow \text{k}\le \text{87,7}\Rightarrow {{\text{k}}_{\text{max}}}=87$ Do đó tần số lớn nhất là : ${{\text{f}}_{\text{max}}}=19,83$kHz. Chọn D.

Bài tập 2: Cho hai nguồn sóng âm kết hợp A, B đặt cách nhau 2 m dao động cùng pha nhau. Di chuyển trên đoạn AB, người ta thấy có 5 vị trí âm có độ to cực đại. Cho biết tốc độ truyền âm trong không khí là 350 m/s. Tần số f của nguồn âm có giá trị thoả mãn A. 350 Hz ≤ f ≤ 525 Hz B. 175 Hz < f < 626,5 Hz C. 350 Hz < f < 525 Hz D. 175 Hz ≤ f < 262,5 Hz

Lời giải chi tiết:

Gọi O là trung điểm của 2 nguồn suy ra O là cực đại ( Do 2 nguồn cùng pha )

Khoảng các giữa 2 cực đại trên AB là $\text{i = }\frac{\lambda }{2}$.

Để có 5 cực đại trên AB thì mỗi bên có 2 cực đại suy ra khoảng cách từ nguồn đến O là:

$2\frac{\lambda }{2}<\text{d3}\frac{\lambda }{2}\Leftrightarrow \frac{350}{\text{f}}<1<1,5.\frac{350}{\text{f}}\Rightarrow 350<\text{f 525}\text{.}$Chọn C.

Bài tập 3: Cột khí trong ống thủy tinh có độ cao $\ell $ có thể thay đổi được nhờ điều chỉnh mực nước trong ống. Đặt một âm thoa trên miệng ống thủy tinh đó. Khi âm thoa dao động, nó phát ra âm cơ bản, ta thấy trong cột khí có một sóng dừng ổn định. Khi độ cao của cột khí nhỏ nhất ${{\ell }_{0}}=13\,cm$ ta nghe được âm to nhất, biết đầu A hở là một bụng sóng, đầu B là nút sóng, tốc độ truyền âm là 340 m/s. Tần số âm do âm thoa phát ra là: A. 563,8 Hz B. 658 Hz C. 653,8 Hz D. 365,8 Hz

Lời giải chi tiết:

Khoảng các từ bụng sóng đến nút liền kề là $\frac{\lambda }{4}$

Khi đó: ${{\ell }_{0}}=\frac{\lambda }{4}=13\text{ cm }\Rightarrow \lambda \text{=52 cm}\Rightarrow \text{f = }\frac{\text{v}}{\lambda }=\frac{340}{0,52}=653,8$Hz. Chọn C.

Bài tập 4: Hai nguồn âm nhỏ S1, S2 giống nhau (được coi là hai nguồn kết hợp) phát ra âm thanh cùng pha và cùng biên độ. Một người đứng ở điểm N với S1N = 3m và S2N = 3,375m. Tốc độ truyền âm trong không khí là 330 m/s. Tìm bước sóng dài nhất để người đó ở N không nghe được âm thanh từ hai nguồn S1, S2 phát ra: A. $\lambda =1\text{ m}$ B. $\lambda =0,5\text{ m}$ C. $\lambda =0,4\text{ m}$  D.$\lambda =0,75\text{ m}$

Lời giải chi tiết:

Để ở N không nghe được âm thì tại N là cực tiểu giao thoa. Do 2 nguồn ngược pha nên tại N sóng âm có biên độ cực tiểu khi: ${{\text{d}}_{1}}-{{\text{d}}_{2}}=(\text{k+0,5)}\lambda \Rightarrow \lambda \text{=}\frac{0,375}{\text{k+0,5}}$

Bước sóng dài nhất ứng với ${{\text{k}}_{\min }}=0\Rightarrow \lambda =0,75\text{ cm}$. Chọn D.

 

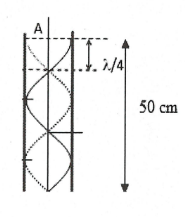
Bài tập 5: Một âm thoa có tần số dao động riêng 850 Hz được đặt sát miệng một ống nghiệm hình trụ đáy kín đặt thắng đứng cao 80 cm. Đổ dần nước vào ống nghiệm đến độ cao 30 cm thì thấy âm được khuếch đại lên rất mạnh. Biết tốc độ truyền âm trong không khí có giá trị nằm trong khoảng 300 m/s ≤  v ≤ 350 m/s. Hỏi khi tiếp tục đồ nước thêm vào ống thì có thêm mấy vị trí của mực nước cho âm được khuếch đại mạnh? A. 1. B. 2. C. 3. D. 4.

Lời giải chi tiết:

Trong ống nghiệm có một đầu bịt kín và một đầu để hở. Ta có: $\ell =(\text{k + 0,5)}\frac{\lambda }{2}=(\text{k + 0,5)}\frac{\text{v}}{2\text{f}}\Rightarrow \text{v =}\frac{2\ell \text{f}}{\text{k + 0,5}}$ $\Rightarrow \text{v =}\frac{510}{\text{k + 0,5}}$. Do $\text{300 m/s }\le \text{ v }\le \text{ 350 m/s}$ $\Rightarrow \left\{ \begin{array}{} \text{k = 1} \\ {} \text{v = 340 m/s} \\ \end{array} \right.\Rightarrow \ell =\frac{\lambda }{4}+\frac{\lambda }{2}$ Chiều cao còn lại của cột nước là 50 cm.

Khi tiếp tục đổ nước vào ống thì chiều đài cột kí giảm dần, và để âm khuyếch đại mạnh thì chiều dài cột khí phải thỏa mãn: $0<\frac{\lambda }{4}+k\frac{\lambda }{2}<50\Leftrightarrow -0,5<k<2\Rightarrow \text{k =0,1}$

Vậy khi đổ thêm nước thì có thêm 2 vị trí làm cho âm khuyếch đại rất mạnh. Chọn B.

 

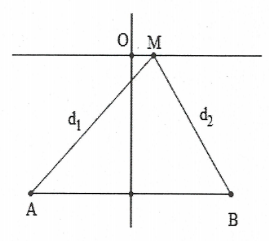
Bài tập 6: Hai nguồn âm điểm phát sóng cầu đồng bộ với tần số f = 680 Hz được đặt tại A và B cách nhau 1m trong không khí. Biết tốc độ truyền âm trong không khí là v = 340 m/s. Bỏ qua sự hấp thụ âm của môi trường. Gọi O là điểm nằm trên đường trung trực của AB cách AB 100m và M là điểm nằm trên đường thẳng qua O song song với AB, gần O nhất mà tại đó nhận được âm to nhất. Khoảng cách OM gần bằng: A. 40 m. B. 50 m. C. 60 m. D. 70 m.

Lời giải chi tiết:

Bước sóng: $\lambda =\frac{\text{v}}{\text{f}}=0,5\text{m}$ Tại M nghe to nhất và gần O nhất thì M nằm trên cực đại số 1 với k = 1. Suy ra: $MA\text{ }\text{ }MB\text{ }=\lambda .$ Mặt khác: $\text{MA=}\sqrt{{{\text{h}}^{2}}+{{\left( \frac{\text{AB}}{2}+\text{OM} \right)}^{2}}}$ $\text{MB=}\sqrt{{{\text{h}}^{2}}+{{\left( \frac{\text{AB}}{2}\text{ - OM} \right)}^{2}}}$(với h = 100m). Do đó $\sqrt{{{100}^{2}}+{{(x+0,5)}^{2}}}-\sqrt{{{100}^{2}}+{{(x-0,5)}^{2}}}=0,5$        SHIFT-CALC      $\text{x = 57,74 m}$. Chọn C.

Dạng 3: Xác định Cường độ âm – Mức cường độ âm.

PHƯƠNG PHÁP GIẢI

▪ Cường độ âm: $\text{I=}\frac{\text{W}}{\text{t}\text{.S}}\text{=}\frac{\text{P}}{\text{S}}$ ( đơn vị W/m²).

Cường độ âm I tại một điểm là đại lượng đo bằng năng lượng mà sóng âm tải qua đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian.

▪ Cường độ âm tại một điểm cách nguồn một đoạn R: $\text{I=}\frac{\text{P}}{\text{4 }\!\!\pi\!\!\text{ }{{\text{R}}^{\text{2}}}}$( đơn vị W/m²).

Với W(J), P(W) là năng lượng, công suất phát âm của nguồn, S (m²) là diện tích mặt vuông góc với phương truyền âm (với sóng cầu thì S là diện tích mặt cầu $\text{S=4 }\!\!\pi\!\!\text{ }{{\text{R}}^{\text{2}}}$)

▪ Mức cường độ âm:

$\text{L(B)=log}\frac{\text{I}}{{{\text{I}}_{\text{0}}}}\Rightarrow \frac{\text{I}}{{{\text{I}}_{\text{0}}}}\text{=1}{{\text{0}}^{\text{L}}}$ Hoặc $\text{L(dB)=10log}\frac{\text{I}}{{{\text{I}}_{\text{0}}}}$

$\begin{array}{} \Rightarrow {{\text{L}}_{\text{2}}}-{{\text{L}}_{\text{1}}}\text{=log}\frac{{{\text{I}}_{\text{2}}}}{{{\text{I}}_{\text{0}}}}-\text{log}\frac{{{\text{I}}_{\text{1}}}}{{{\text{I}}_{\text{0}}}}\text{=log}\frac{{{\text{I}}_{\text{2}}}}{{{\text{I}}_{\text{1}}}}\Leftrightarrow\frac{{{\text{I}}_{\text{2}}}}{{{\text{I}}_{\text{1}}}}\text{=1}{{\text{0}}^{{{\text{L}}_{\text{2}}}-{{\text{L}}_{\text{1}}}}} \\ {}  \\ \end{array}$.

Với ${{\text{I}}_{\text{0}}}\text{=1}{{\text{0}}^{\text{-12}}}$ W/m² gọi là cường độ âm chuẩn ở f = 1000 Hz.

Đơn vị của mức cường độ âm là Ben (B), thường dùng đềxiben (dB): 1B = 10dB

▪ Cường độ âm tại A, B cách nguồn O: $\frac{{{I}_{A}}}{{{I}_{B}}}=\frac{O{{B}^{2}}}{O{{A}^{2}}}$

Càng xa nguồn âm cường độ âm giảm tỉ lệ nghịch với bình phương khoảng cách.

Tai người cảm thụ được âm: 0 dB đến 130 dB.

▪ Xây dựng một số công thức

Ta có: $I=\frac{P}{4\pi R_{{}}^{2}}\Rightarrow \left\{ \begin{array}{} {{I}_{1}}=\frac{P}{4\pi R_{1}^{2}} \\ {} {{I}_{2}}=\frac{P}{4\pi R_{2}^{2}} \\ \end{array} \right.\Rightarrow {{L}_{2}}-{{L}_{1}}=\log \frac{{{I}_{2}}}{{{I}_{1}}}=\log \frac{{{P}_{2}}}{{{P}_{1}}}-2\log \frac{{{R}_{2}}}{{{R}_{1}}}(B)=10\log \frac{{{P}_{2}}}{{{P}_{1}}}-20\log \frac{{{R}_{2}}}{{{R}_{1}}}(dB).$

Nếu công suất nguồn âm không đổi thì ${{L}_{2}}-{{L}_{1}}=10\lg \frac{{{I}_{2}}}{{{I}_{1}}}=20.\lg \frac{{{R}_{1}}}{{{R}_{2}}}(dB).$

Đặt n nguồn âm giống nhau cùng công suất P₀ thì công suất nguồn coi là P = nP₀.

BÀI TẬP MINH HỌA DẠNG 3

Bài tập 1: Hai âm có mức cường độ âm chênh lệch nhau là 20 đB. Tỉ số cường độ âm của chúng là: A. 100 B. 200 C. 400 D. 1020

Lời giải chi tiết:

Theo bài ra ta có: ${{L}_{A}}-{{L}_{B}}=20dB\Leftrightarrow 10\log \frac{{{I}_{A}}}{{{I}_{B}}}=20\Rightarrow \frac{{{I}_{A}}}{{{I}_{B}}}={{10}^{2}}.$ Chọn A.

Bài tập 2: Khi cường độ âm gấp 100 lần cường độ âm chuẩn thì mức cường độ âm có giá trị là: A. L = 2 dB B. L = 20 dB C. L = 20 B D. L = 100 dB

Lời giải chi tiết:

Ta có: $L(dB)=10\log \frac{I}{{{I}_{0}}}=10\log 100=20dB.$ Chọn B.

Bài tập 3: [Trích đề thi THPT QG năm 2017]. Biết cường độ âm chuẩn là 10-12 W /m2. Khi cường độ âm tại một điểm là 10-5 W /m2 thì mức cường độ âm tại điểm đó là: A. 9 B B. 7 B C. 12 B D. 5 B

Lời giải chi tiết:

Ta có: $L=\log \frac{I}{{{I}_{0}}}=\log \frac{{{10}^{-5}}}{{{10}^{-12}}}=7(B).$ Chọn B.

Bài tập 4: Mức cường độ âm tại vị trí cách loa 1m là 55 dB. Một người xuất phát từ loa, đi ra xa nó thì thấy rằng khi cách loa 100 m thì không còn nghe được âm do loa đó phát ra nữa. Lấy cường độ âm chuẩn là ${{I}_{0}}={{10}^{-12}}W/{{m}^{2}},$ coi sóng âm do loa đó phát ra là sóng cầu. Xác định ngưỡng nghe của tai người này. A. 15 dB B. 95 dB C. 10 dB D. 100 dB

Lời giải chi tiết:

Ta có: ${{I}_{1}}=\frac{P}{4\pi R_{1}^{2}};{{I}_{2}}=\frac{P}{4\pi R_{2}^{2}}\Rightarrow {{L}_{2}}-{{L}_{1}}=\log \frac{{{I}_{2}}}{{{I}_{1}}}=20\log \frac{{{R}_{1}}}{{{R}_{2}}}=20\log \frac{1}{100}=-40(dB)$

$\Rightarrow {{L}_{2}}={{L}_{1}}-40=15dB.$ Chọn A.

Bài tập 5: Một nguồn O phát sóng âm có công suất không đổi trong một môi trường đắng hướng và không hấp thụ âm. Tại điểm A, mức cường độ âm là 40 dB. Nếu tăng công suất của nguồn âm lên 4 lần nhưng không đổi tần số thi mức cường độ âm tại A là: A. 52 dB B. 67 dB C. 46 dB D. 160 dB

Lời giải chi tiết:

Ta có: $I=\frac{P}{4\pi R_{{}}^{2}}\Rightarrow \left\{ \begin{array}{} {{I}_{1}}=\frac{P}{4\pi R_{1}^{2}} \\ {} {{I}_{2}}=\frac{P}{4\pi R_{2}^{2}} \\ \end{array} \right.\Rightarrow {{L}_{2}}-{{L}_{1}}=\log \frac{{{I}_{2}}}{{{I}_{1}}}=\log \frac{{{P}_{2}}}{{{P}_{1}}}=\log 4.$

Do đó: ${{L}_{2}}=\log 4+40=46dB.$Chọn C.

Bài tập 6: [Trích đề thi THPT QG năm 2017]. Một nguồn âm đẳng hướng với công suất không đổi trong một môi trường hập thụ và phản xạ âm. Lúc đầu, mức cường độ âm đo S gây ra tại điểm M là L (dB). Khi cho S tiến lại gần M thêm một đoạn 60 m thì mức cường độ âm tại M lúc này là L+6 (dB). Khoảng cách từ S đến M lúc đầu là: A. 80,6 m B. 120,3 m C. 200 m D. 40 m

 

Lời giải chi tiết:

Ta có: ${{L}_{2}}-{{L}_{1}}=20\log \frac{{{R}_{2}}}{{{R}_{1}}}=-6\Leftrightarrow 20\log \frac{{{R}_{1}}-60}{{{R}_{1}}}=6\Leftrightarrow 1-\frac{60}{{{R}_{1}}}=0,49888\Rightarrow {{R}_{1}}=120,3m.$

Chọn B.

Bài tập 7: Nguồn âm đặt tại O có công suất truyền âm không đổi. Trên cùng nửa đường thắng qua O có ba điểm A, B, C theo thứ tự có khoảng cách tới nguồn tăng dần. Mức cường độ âm tại B kém mức cường độ âm tại A là b (B); mức cường độ âm tại B hơn mức cường độ âm tại C là 3b (B). Biết 4OA = 3OB. Coi sóng âm là sóng cầu và môi trường truyền âm đẳng hướng. Tỉ số $\frac{OC}{OA}$ bằng: A. $\frac{346}{56}$ B. $\frac{256}{81}$ C. $\frac{276}{21}$ D. $\frac{16}{9}$

Lời giải chi tiết:

Ta có: ${{L}_{A}}-{{L}_{B}}=\log \frac{{{I}_{A}}}{{{I}_{B}}}=2\log \frac{{{R}_{B}}}{{{R}_{A}}}=b\Rightarrow 2\log \frac{4}{3}=b.$

Lại có: ${{L}_{B}}-{{L}_{C}}=\log \frac{{{I}_{B}}}{{{I}_{A}}}=2\log \frac{{{R}_{C}}}{{{R}_{B}}}=3b=6\log \frac{4}{3}\Rightarrow \frac{{{R}_{C}}}{{{R}_{B}}}=\frac{64}{27}\Rightarrow \frac{{{R}_{C}}}{\frac{4}{3}{{R}_{A}}}=\frac{64}{27}.$

Do đó $\frac{{{R}_{C}}}{{{R}_{A}}}=\frac{256}{81}.$ Chọn B.

Bài tập 8: [Trích đề thi đại học năm 2012]: Tại điểm O trong môi trường đẳng hướng, không hấp thụ âm, có 2 nguồn âm điểm, giống nhau với công suất phát âm không đổi. Tại điểm A có mức cường độ âm 20 dB. Đề tại trung điểm M của đoạn OA có mức cường độ âm là 30 dB thì số nguồn âm giống các nguồn âm trên cần đặt thêm tại O bằng: A. 4 B. 3 C. 5 D. 7

Lời giải chi tiết:

Gọi P₀ là công suất của một nguồn âm điểm, n là số nguồn âm đặt tại O lần sau.

Ta có: ${{L}_{2}}-{{L}_{1}}=10\log \frac{{{P}_{2}}}{{{P}_{1}}}-20\log \frac{{{R}_{2}}}{{{R}_{1}}}=10\log \frac{n{{P}_{0}}}{2{{P}_{0}}}-20\log \frac{{{R}_{M}}}{{{R}_{A}}}=10(dB).$

Khi đó $10\log \frac{n}{2}-20\log \frac{1}{2}=10\Rightarrow n=5.$

Vậy cần đặt thêm 3 nguồn âm tại O. Chọn B.

Bài tập 9: Trong buổi hòa nhạc được tổ chức ở Nhà Hát lớn Hà Nội nhân dịp kỉ niệm 1000 năm Thăng Long. Một người ngồi dưới khán đài nghe được âm do một chiếc đàn giao hưởng phát ra có mức cường độ âm 12 dB. Khi dàn nhạc giao hưởng thực hiện bản hợp xướng người đó cảm nhận được âm là 2,376 B. Hỏi dàn nhạc giao hưởng đó có bao nhiêu người? A. 8 người B. 18 người C. 12 người D. 15 người

Lời giải chi tiết:

Ban đầu có 1 nguồn âm. Khi thực hiện bản hợp xướng có n người ( hay n nguồn âm).

Ta có: ${{L}_{2}}-{{L}_{1}}=10\log \frac{{{P}_{2}}}{{{P}_{1}}}=10\log \frac{n{{P}_{1}}}{{{P}_{1}}}=10\log n=23,76-12.$ Do đó $n=15.$ Chọn C.

Bài tập 10: Một nguồn âm được coi là nguồn điểm phát sóng cầu và môi trường không hấp thụ âm. Tại một vị trí sóng âm có biên độ 0,12 mm có cường độ âm tại điểm đó bằng 1,80 W/m2. Hỏi tại vị trí sóng có biên độ bằng 0,36 mm thì sẽ có cường độ âm tại điểm đó bằng bao nhiêu ? A. 0,60 W/m2 B. 2,70 W/m2 C. 5,40 W/m2 D. 16,2 W/m2

Lời giải chi tiết:

Do nguồn âm được coi là nguồn điểm phát sóng cầu và môi trường không hấp thụ âm, nên năng lượng sóng âm phân bổ đều trên các đường tròn đồng tâm. Các vị trí càng xa nguồn, tức là thuộc mặt cầu có bán kính càng lớn thì năng lượng của sóng âm càng nhỏ, do đó biên độ càng nhỏ.

Do môi trường không hấp thụ âm nên $\frac{{{I}_{1}}}{{{I}_{2}}}=\frac{R_{2}^{2}}{R_{1}^{2}}=\frac{{{\text{W}}_{1}}}{{{\text{W}}_{2}}}=\frac{A_{1}^{2}}{A_{2}^{2}}.$

$\frac{{{I}_{1}}}{{{I}_{2}}}=\frac{A_{1}^{2}}{A_{2}^{2}}\Rightarrow {{I}_{2}}={{I}_{1}}{{\left( \frac{0,36}{0,12} \right)}^{2}}=16,2(\text{W}/{{m}^{2}}).$ Chọn D.

Bài tập 11: Hai điểm M và N nằm ở cùng l phía của nguồn âm trong môi trường đẳng hướng không hấp thụ âm, trên cùng 1 phương truyền âm có LM =30 dB, LN = 10 dB. Nếu nguồn âm đó đặt tại M thì mức cường độ âm tại N khi đó xấp xỷ là: A. 12 dB B. 7 dB C. 9 dB D. 11 dB

Lời giải chi tiết:

Ta có: ${{L}_{M}}-{{L}_{N}}=20\log \frac{ON}{OM}=20\Rightarrow ON=10\,OM.$

Khi đó: $MN=ON-OM=9\,OM.$

Nêu đặt nguồn âm tại M thì ta có: ${{L}_{N}}-{{L}_{N'}}=20\log \frac{R'}{R}=20\log \frac{9.OM}{10.OM}.$

Suy ra: ${{L}_{N'}}=10-20\log 0,9=10,915(dB).$ Chọn D.

Bài tập 12: [Trích đề thi THPT QG năm 2017]. Một nguồn âm đặt tại điểm O phát âm đẳng hướng với công suất không đổi trong một môi trường không hấp thụ và phản xạ âm. Hai điểm M và N cách O lần lượt là r và r – 50 (m) có cường độ âm tương ứng là I và 4I. Giá trị của r bằng: A. 60m B. 66m C. 100m D. 142m

Lời giải chi tiết:

Ta có: $\frac{{{I}_{1}}}{{{I}_{2}}}={{\left( \frac{{{r}_{2}}}{{{r}_{1}}} \right)}^{2}}\Rightarrow \frac{1}{4}={{\left( \frac{r-50}{r} \right)}^{2}}\Rightarrow \frac{1}{2}=1-\frac{50}{r}\Rightarrow r=100m.$

Chọn C.

Bài tập 13: Cho 3 điểm A, B, C thẳng hàng, theo thứ tự xa dần nguồn âm. Mức cường độ âm tại A, B, C lần lượt là 40 dB; 35,9 dB và 30 dB. Khoảng cách giữa AB là 30 m và khoảng cách giữa BC là A. 78m B. 108m C. 40m D. 65m

Lời giải chi tiết:

Ta có: ${{L}_{A}}-{{L}_{B}}=20\log \frac{{{R}_{B}}}{{{R}_{A}}}=4,1\Rightarrow \frac{{{R}_{B}}}{{{R}_{A}}}=\frac{OB}{OA}=1,6.$

Khi đó: $OB-OA=1,6OA-OA=30\Rightarrow OA=50m.$

Lại có: ${{L}_{A}}-{{L}_{C}}=20\log \frac{OC}{OA}=10\Rightarrow OC=\sqrt{10}.OA\Rightarrow AC=(\sqrt{10}-1)OA=108.$

Do đó BC = 78 m. Chọn A.

Bài tập 14: Một nguồn âm S phát ra âm có tần số xác định. Năng lượng âm truyền đi phân phối đều trên mặt cầu tâm S bán kính d. Bỏ qua sự phản xạ của sóng âm trên mặt đất và các vật cản. Tại điểm A cách nguồn âm S một khoảng 100 m, mức cường độ âm là 20 dB. Xác định vị trí điểm B để tại đó mức cường độ âm bằng 0. A. 1000 m B. 100 m C. 10 m D. 1 m

Lời giải chi tiết:

Ta có: ${{L}_{A}}-{{L}_{B}}=20\log \frac{OB}{OA}=20\Rightarrow OB=10OA=1000m.$ Chọn A.

Bài tập 15: Ba điểm A, B, C thuộc nửa đường thẳng từ A. Tại A đặt một nguồn phát âm đằng hướng có công suất thay đổi. Khi $P={{P}_{1}}$ thì mức cường độ âm tại B là 60 dB, tại C là 20 dB. Khi $P={{P}_{2}}$thì mức cường độ âm tại B là 90 dB và mức cường độ âm tại C là A. 50 dB B. 60 dB C. 10 dB D. 40 dB

Lời giải chi tiết:

Ta có: ${{L}_{B}}-{{L}_{C}}=40=20\log \frac{AC}{AB}\Rightarrow \log \frac{AC}{AB}=2.$

Khi thay đổi công suất ta có: ${{L}_{B'}}-{{L}_{C'}}=20\log \frac{AC}{AB}=40\Rightarrow {{L}_{C'}}=50dB.$ Chọn A.

Bài tập 16: Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm. Mức cường độ âm tại M là 70 dB, tại N là 30 dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại trung điểm MN khi đó là: A. 36,1 dB B. 41,2 dB C. 33,4 dB D. 42,1 dB

Lời giải chi tiết

Ta có: ${{L}_{M}}-{{L}_{N}}=20\log \frac{ON}{OM}=40\Rightarrow ON=\operatorname{l}00OM\Rightarrow MN=99OM.$

Nếu chuyển nguồn âm đó sang vị trí M thì $IM=R'=\frac{99OM}{2}$ (với I là trung điểm MN).

Khi đó: ${{L}_{M}}-{{L}_{I}}=20\log \frac{R'}{R}=20\log \frac{49,5OM}{OM}\Rightarrow {{L}_{I}}=36,1dB.$ Chọn A.

Bài tập 17: Một nguồn âm P phát ra âm đẳng hướng. Hai điểm A, B nằm cùng trên một phương truyền sóng có mức cường độ âm lần lượt là 40dB và 30dB. Điểm M nằm trong môi trường truyền sóng sao cho $\Delta AMB$ vuông cân ở A. Xác định mức cường độ âm tại M? A. 37,54 dB B. 32,46 dB C. 35,54 dB D. 38,46 dB

Lời giải chi tiết:

Ta có: ${{L}_{A}}-{{L}_{B}}=20\log \frac{OB}{OA}$ Do đó $OB=\sqrt{10}OA\Rightarrow AB=\left( \sqrt{10}-1 \right)OA.$ $\Rightarrow OM=\sqrt{O{{A}^{2}}+A{{M}^{2}}}=\sqrt{O{{A}^{2}}+{{\left( \sqrt{10}-1 \right)}^{2}}O{{A}^{2}}}$ Do đó $OM=OA\sqrt{12-2\sqrt{10}}.$ Mặt khác ${{L}_{M}}-{{L}_{A}}=20\log \frac{OA}{OM}=20\log \frac{1}{\sqrt{12-2\sqrt{10}}}=-7,54\Rightarrow {{L}_{M}}=32,46.$Chọn B.

Bài tập 18: Nguồn âm tại O có công suất không đổi. trên cùng đường thẳng qua O có ba điểm A, B, C cùng nằm về một phía của O và theo thứ tự xa có khoảng cách tới nguồn tăng dần. Mức cường độ âm tại B kém mức cường độ âm tại A là a (dB), mức cường độ âm tại B hơn mức cường độ âm tại C là 3a (dB). Biết $OA=\frac{2}{3}OB.$ Tính tỉ số $\frac{OC}{OA}:$ A. $\frac{81}{16}$  B. $\frac{9}{4}$ C. $\frac{27}{8}$ D. $\frac{32}{27}$

Lời giải chi tiết:

Ta có: ${{L}_{A}}-{{L}_{B}}=\log \frac{{{I}_{A}}}{{{I}_{B}}}=20\log \frac{OB}{OA}=a\Rightarrow 20\log \frac{3}{2}=a.$

Lại có: ${{L}_{B}}-{{L}_{C}}=\log \frac{{{I}_{B}}}{{{I}_{C}}}=20\log \frac{OC}{OB}=3a=60\log \frac{3}{2}\Rightarrow \frac{OC}{OB}=\frac{27}{8}\Rightarrow \frac{OC}{\frac{3}{2}OA}=\frac{27}{8}.$

Do đó $\frac{OC}{OA}=\frac{81}{16}.$ Chọn A.

Bài tập 19: Mức cường độ âm của một âm là L=30 (dB). Hãy tính cường độ âm này theo đơn vị W/m2. Biết cường độ âm chuẩn là ${{I}_{0}}={{10}^{-12}}\left( \text{W}/{{m}^{2}} \right).$ Mức cường độ âm tính theo đơn vị (dB) là: A. ${{10}^{-18}}\text{W}/{{m}^{2}}.$ B. ${{10}^{-9}}\text{W}/{{m}^{2}}.$ C. ${{10}^{-3}}\text{W}/{{m}^{2}}.$              D. ${{10}^{-4}}\text{W}/{{m}^{2}}.$

Lời giải chi tiết:

Ta có: $10\log \frac{I}{{{I}_{0}}}=30\Rightarrow I={{10}^{3}}{{I}_{0}}={{10}^{-9}}^{{}}W/{{m}^{2}}.$ Chọn B.

Bài tập 20: [Trích đề thi THPT QG năm 2017]. Cho 4 điểm O, M, N và P nằm trong một môi trường truyền âm. Trong đó, M và N nằm trên nửa đường thẳng xuất phát từ O, tam giá MNP là tam giác đều. Tại O, đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại M và N lần lượt là 50 dB và 40 dB. Mức cường độ âm tại P là A.  43,6 dB B. 38,8 dB C. 35,8 dB D. 41,1 dB

Lời giải chi tiết:

Ta có: ${{L}_{M}}-{{L}_{N}}=20\log \frac{ON}{OM}\Rightarrow ON=\sqrt{10}OM.$

Khi đó $MN=ON-OM=\left( \sqrt{10}-1 \right)OM.$

Đặt $OM=a\Rightarrow MN=a\left( \sqrt{10}-1 \right),ON=a\sqrt{10}.$

Khi đó:

$MH=\frac{\sqrt{10}-1}{2}a;PH=\frac{\left( \sqrt{10}-1 \right)a\sqrt{3}}{2}\Rightarrow OP=\sqrt{P{{H}^{2}}+O{{H}^{2}}}=2,8a.$

Ta có: ${{L}_{P}}-{{L}_{M}}=20\log \frac{OM}{OP}=20\log \frac{1}{2,8}\Rightarrow {{L}_{P}}=41,1dB.$ Chọn D.

Bài tập 21: [Trích đề thi THPT QG năm 2015]. Tại vị trí O trong một nhà máy, một còi báo cháy (xem là nguồn điểm) phát âm với công suất không đổi. Từ bên ngoài, một thiết bị xác định mức cường độ âm chuyển động thẳng từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 0,4 m/s2 cho đến khi dừng lại tại N (cổng nhà máy). Biết NO = 10m và mức cường độ âm (do còi phát ra) tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm đẳng hướng và không hấp thụ âm. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất sau đây? A.  27 s B. 32 s C. 47 s D. 25 s

Lời giải chi tiết:

Ta có: ${{L}_{M}}-{{L}_{N}}=20\log \frac{ON}{OM}\Rightarrow OM=10ON.$

Do đó $MN=OM-ON=9ON=90m.$

Vật đi từ M đến trung điểm của MN, sau đó chuyển động chậm dần đều và dừng lại tại N nên ta có: ${{t}_{MN}}=2{{t}_{MC}}.$

Mặt khác $MC=\frac{1}{2}a{{t}^{2}}\Rightarrow {{t}_{MC}}=\sqrt{\frac{2MC}{a}}\Rightarrow {{t}_{MN}}=\sqrt{\frac{MN}{a}}=30s.$

Vậy giá trị gần nhất là 32 s. Chọn B.

Bài tập 21: [Trích đề thi đại học năm 2014]. Để ước lượng độ sâu của một giếng cạn nước, một người dùng đồng hồ bấm giây, ghé sát tai vào miệng giếng và thả một hòn đá rơi tự do từ miệng giếng; sau 3s thì người đó nghe thấy tiếng hòn đá đập vào đáy giếng. Giả sử tốc độ truyền âm trong không khí là 330 m/s, lấy g = 9,9 m/s2. Độ sâu ước lượng của giếng là: A.  39m B. 43m C. 41m D. 45m

Lời giải chi tiết:

Gọi h là độ sâu của giếng ta có:

Thời gian rơi tự do của hòn đá là: $h=\frac{1}{2}gt_{1}^{2}\Rightarrow {{t}_{1}}=\sqrt{\frac{2h}{g}}.$

Thời gian sóng âm truyền từ đáy giếng tới tai là: $h={{v}_{2}}{{t}_{2}}\Rightarrow {{t}_{2}}=\frac{h}{330}.$

Ta có: ${{t}_{1}}+{{t}_{2}}=\frac{\sqrt{2h}}{\sqrt{0,99}}+\frac{h}{330}=3\Rightarrow h\approx 41m.$ Chọn C.

Bài tập 21: [Trích đề thi đại học năm 2013]. Trên một đường thẳng cố định trong môi trường đẳng hướng, không hấp thụ và phản xạ âm, một máy thu ở cách nguồn âm một khoảng d thu được âm có mức cường độ âm là L; khi dịch chuyển máy thu ra xa nguồn âm thêm 9m thì mức cường độ âm thu được là $L-20\,\,(dB)$. Khoảng cách d là A.  1 m B. 9 m C. 8 m D. 10 m

Lời giải chi tiết:

Ta có: ${{L}_{1}}-{{L}_{2}}=20=20\log \frac{{{R}_{2}}}{{{R}_{1}}}\Leftrightarrow \frac{{{R}_{1}}+9}{{{R}_{1}}}=10\Rightarrow {{R}_{1}}=1m.$Chọn A.

Bài tập 22: [Trích đề thi đại học năm 2011]. Một nguồn điểm O phát sóng âm có công suất không đổi trong một môi trường truyền âm đẳng hướng và không hấp thụ âm. Hai điểm A, B cách nguồn âm lần lượt là r1 và r2. Biết cường độ âm tại A gấp 4 lần cường độ âm tại B. Tỉ số $\frac{{{r}_{2}}}{{{r}_{1}}}$  bằng : A. 2 B. $\frac{1}{2}$  C. 4 D. $\frac{1}{4}$

Lời giải chi tiết:

Ta có: $I=\frac{P}{4\pi {{R}^{2}}}\Rightarrow \frac{{{I}_{A}}}{{{I}_{B}}}=\frac{r_{2}^{2}}{r_{1}^{2}}=4\Rightarrow \frac{{{r}_{2}}}{{{r}_{1}}}=2.$ Chọn A.

Bài tập 23: [Trích đề thi đại học năm 2010]. Ba điểm O, A, B cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng trong không gian, môi trường không hấp thụ âm. Mức cường độ âm tại A là 60 dB, tại B là 20 dB. Mức cường độ âm tại trung điểm M của đoạn AB là: A.  40 dB B. 34 dB  C. 26 dB D. 17 dB

Lời giải chi tiết:

Ta có: ${{L}_{A}}-{{L}_{B}}=20\log \frac{{{R}_{B}}}{{{R}_{A}}}=40\Rightarrow {{R}_{B}}=100{{R}_{A}}.$

Mặt khác ${{R}_{M}}=\frac{{{R}_{A}}+{{R}_{B}}}{2}=50,5{{R}_{A}}$

Suy ra ${{L}_{A}}-{{L}_{M}}=20\log \frac{{{R}_{M}}}{{{R}_{A}}}=20\log \frac{50,5{{R}_{A}}}{{{R}_{A}}}\Rightarrow {{R}_{M}}=60-20\log 50,5=26dB.$ Chọn C.

Bài tập 24: [Trích đề thi đại học Vinh lần 1 - 2017]. Xét 2 điểm M, N ở trong môi trường đàn hồi có sóng âm phát ra từ nguồn S truyền qua. Biết S, M, N thẳng hàng và SN = 2SM. Ban đầu, mức cường độ âm tại M là L (dB). Nếu công suất của nguồn phát tăng lên 100 lần thì mức cường độ âm tại điểm N bằng A.  L+14 (dB) B. L-14 (dB) C. $\frac{L}{2}$ (dB) D. L-20 (dB)

Lời giải chi tiết:

Ta có: ${{L}_{N}}-{{L}_{M}}=10\log \frac{I'}{I}+20\log \frac{SM}{SN}=20+20\log 0,5=14\Rightarrow {{L}_{N}}=L+14.$

Chọn A.

Bài tập 25: [Trích đề thi đại học Vinh lần 3 - 2017]. Trong môi trường đẳng hướng và không hấp thụ âm, trên mặt phẳng nằm ngang có 3 điểm O, M, N tạo thành tam giác vuống tại O, với OM = 80m, ON = 60m. Đặt tại O một nguồn điểm phát âm công suất P không đổi thì mức cường độ âm tại M là 50 dB. Mức cường độ âm lớn nhất trên đoạn MN xấp xỉ bằng A.  80,2 dB B. 50 dB C. 65,8 dB D. 54,4 dB

Lời giải chi tiết:

Áp dụng hệ thức lượng trong tam giác vuông OMN

Ta có: $OH=\frac{OM.ON}{\sqrt{O{{M}^{2}}+O{{N}^{2}}}}=48cm.$

Ta có: ${{L}_{H}}-{{L}_{M}}=20\log \frac{OM}{OH}=20\log \frac{80}{48}$

Suy ra ${{L}_{H}}=50+20\log \frac{80}{48}=54,4dB.$ Chọn D.

Bài tập 25: [Trích đề thi chuyên Quốc Học Huế 2017]. Trong đêm văn nghệ kỉ niệm 120 năm thành lập trường Quốc Học. Mở màn văn nghệ là lớp 12 Anh, coi mọi học sinh đều hát với cùng cường độ âm và cùng tần số. Khi một học sinh hát thì mức cường độ âm là 68 dB. Khi cả lớp cùng hát thì đo được mức cường độ âm là 80 dB. Số học sinh lớp 12 Anh có trong tốp ca này là: A.  16 người B. 12 người C. 10 người D. 16 người

Lời giải chi tiết:

Ban đầu có 1 nguồn âm. Khi cả lớp cùng hát có n người (hay n nguồn âm).

Ta có: ${{L}_{2}}-{{L}_{1}}=10\log \frac{{{P}_{2}}}{{{P}_{1}}}=10\log \frac{n{{P}_{1}}}{{{P}_{1}}}=10\log n=80-68=12.$ Do đó n=16. Chọn A.

Bài tập 26: Ba điểm S, A, B nằm trên một đường tròn đường kính AB biết $AB=\sqrt{2}SA$. Tại S đặt một nguồn âm đẳng hướng thì mức cường độ âm tại B là 40 dB. Mức cường độ âm tại trung điểm AB là? A.  41,51 dB B. 44,77 dB C. 43,01 dB D. 36,99 dB

Lời giải chi tiết:

Dựa vào hình vẽ ta có $\left\{ \begin{array}{} AB=2R \\ {} AB=\sqrt{2}SA \\ \end{array} \right.\Rightarrow SA=SB=R\sqrt{2}$

Gọi O là trung điểm của AB$\Rightarrow SO=R$

Ta có $\frac{P}{4\pi d}={{I}_{0}}{{10}^{L}}\Rightarrow {{\left( \frac{SB}{SO} \right)}^{2}}=\frac{{{10}^{{{L}_{O}}}}}{{{10}^{{{L}_{B}}}}}\Leftrightarrow {{\left( \frac{1}{\sqrt{2}} \right)}^{2}}=\frac{{{10}^{{{L}_{O}}}}}{{{10}^{4}}}$

$\Rightarrow {{10}^{{{L}_{O}}}}=5000\Rightarrow {{L}_{O}}=3,699B=36,99dB.$ Chọn D.

Bài tập 27: Cho 4 điểm O, A, B, C theo thứ tự đó cùng nằm trên một đường thẳng. Tại O đặt một nguồn âm điểm phát sóng đẳng hướng. Mức cường độ âm tại A lớn hơn mức cường độ âm tại B là 20 dB, mức cường độ âm tại B lớn hơn mức cường độ âm tại C là 20dB. Tỉ số AB/BC A.  10 B. 1/10 C. 9 D. 1/9

Lời giải chi tiết:

Ta có $\frac{P}{4\pi {{d}^{2}}}={{I}_{0}}{{10}^{L}}\Rightarrow {{\left( \frac{OB}{OA} \right)}^{2}}=\frac{{{10}^{{{L}_{A}}}}}{{{10}^{{{L}_{B}}}}}={{10}^{{{L}_{A}}-{{L}_{B}}}}={{10}^{2}}\Rightarrow OB=10OA.$

Tiếp tục ta có ${{\left( \frac{OC}{OB} \right)}^{2}}=\frac{{{10}^{{{L}_{B}}}}}{{{10}^{{{L}_{C}}}}}\Leftrightarrow {{\left( \frac{OC}{OA} \right)}^{2}}={{10}^{{{L}_{B}}-{{L}_{C}}}}={{10}^{2}}\Leftrightarrow OC=10OB$

Chọn $OA=1\Rightarrow \left\{ \begin{array}{} OB=10 \\ {} OC=100 \\ \end{array} \right.\Rightarrow AB=OB-OA=9$ và $BC=OC-OB=90\Rightarrow \frac{AB}{BC}=\frac{1}{10}.$ Chọn B.

Bài tập 28: [Trích đề thi thử Chuyên KHTN – 2016]. Tại vị trí O trên mặt đất, người ta đặt một nguồn phát âm với công suất không đổi. Một thiết bị xác định mức cường độ âm chuyển động từ M đến N. Mức cường độ âm của âm phát ra từ O do máy thu được trong quá trình chuyển động từ 45 dB đến 50 dB rồi giảm về 40 dB. Các phương OM và ON hợp với nhau một góc khoảng? A.  $127{}^\circ $  B. $68{}^\circ $ C. $90{}^\circ $ D. $142{}^\circ $

Lời giải chi tiết:

Dựa vào hình vẽ $\Rightarrow $ H là điểm có khoảng cách ngắn nhất nên L_H = 50dB.

Ta có $\frac{P}{4\pi {{d}^{2}}}={{I}_{0}}{{10}^{L}}\Rightarrow {{\left( \frac{ON}{OH} \right)}^{2}}=\frac{{{10}^{{{L}_{H}}}}}{{{10}^{{{L}_{M}}}}}=\frac{{{10}^{5}}}{{{10}^{4}}}\Leftrightarrow \frac{ON}{OH}=\sqrt{10}.$

Chọn $OH=1\Rightarrow ON=\sqrt{10}$

Mặt khác ${{\left( \frac{OM}{OH} \right)}^{2}}=\frac{{{10}^{{{L}_{H}}}}}{{{10}^{{{L}_{M}}}}}=\frac{{{10}^{5}}}{{{10}^{4,5}}}=1,78\Rightarrow OM=1,78$

Ta có $\left\{ \begin{array}{} MH=1,47 \\ {} NH=3 \\ \end{array} \right.\Rightarrow MN=4,47\Rightarrow c\text{os}\widehat{MON}\text{=}\frac{O{{M}^{2}}+O{{N}^{2}}-M{{N}^{2}}}{2OMON}=127{}^\circ $ . Chọn A.

Bài tập 29: Nguồn âm điểm O phát sóng đẳng hướng ra môi trường không hấp thụ và không phản xạ. Điểm M cách nguồn âm một khoảng R có mức cường độ âm 20dB. Tăng công suất nguồn âm lên n lần thì mức cường độ âm tại N cách nguồn âm một khoảng R/2 là 16 dB. Giá trị của n là? A.  8 B. 4,5 C. 2,5 D. 10

Lời giải chi tiết:

Ta có $\frac{P}{4\pi {{d}^{2}}}={{I}_{0}}{{10}^{L}}\Rightarrow \frac{P}{nP}{{\left( \frac{ON}{OM} \right)}^{2}}=\frac{{{10}^{{{L}_{M}}}}}{{{10}^{{{L}_{N}}}}}\Leftrightarrow \frac{1}{n}.{{\left( \frac{1}{2} \right)}^{2}}=\frac{{{10}^{2}}}{{{10}^{3,6}}}\Leftrightarrow n=9,95\approx 10.$ Chọn C.

Bài tập 30: Một dàn loa phát âm đẳng hướng. Mức cường độ âm đo được tại các điểm cách loa một khoảng a và 5a lần lượt là 100 dB và L. Giá trị của L là? A. 100 dB B. 39 dB C. 86 dB D. 25 dB

Lời giải chi tiết

Ta có $\frac{P}{4\pi {{d}^{2}}}={{I}_{o}}{{10}^{L}}\Rightarrow {{\left( \frac{{{d}_{1}}}{{{d}_{2}}} \right)}^{2}}=\frac{{{10}^{{{L}_{2}}}}}{{{10}^{{{L}_{1}}}}}\Leftrightarrow {{\left( \frac{1}{5} \right)}^{2}}=\frac{{{10}^{L}}}{{{10}^{10}}}\Rightarrow {{10}^{L}}=\frac{{{10}^{10}}}{25}\Rightarrow L=8,6\,dB=86\,B.$Chọn C.