Lý thuyết về giao thoa sóng cơ

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1. Hiện tượng giao thoa của hai sóng trên mặt nước

* Hai nguồn điện kết hợp là:

+) Hai nguồn sóng dao động cùng phương, cùng tần số.

+) Có hiệu số pha không đổi theo thời gian.

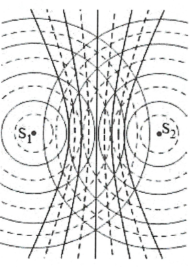
* Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau; có những điểm ở đó chúng luôn luôn triệt tiêu nhau.

Trong hình vẽ bên, những điểm dao động mạnh nhất hợp thành những đường Hypebol nét liền và những điểm dao động với biên độ cực tiểu tạo thành những đường Hypebol nét đứt.

2. Dao động của một điểm trong vùng giao thoa.

Giao thoa của hai sóng phát ra từ hai nguồn kết hợp ${{S}_{1}}$, ${{S}_{2}}$.

Xét hai nguồn sóng kết hợp ${{u}_{1}}={{A}_{1}}\text{cos}\left( \omega t+{{\varphi }_{1}} \right)$ và ${{u}_{2}}={{A}_{2}}\text{cos}\left( \omega t+{{\varphi }_{2}} \right)$.

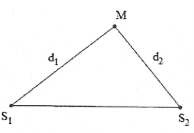
Gọi M là một điểm trong vùng giao thoa. Điểm M lần lượt cách ${{S}_{1}}$, ${{S}_{2}}$ những khoảng ${{d}_{1}}={{S}_{1}}M$ và ${{d}_{2}}={{S}_{2}}M$.

Phương trình sóng do ${{u}_{1}}$, ${{u}_{2}}$ truyền tới M là:

${{u}_{1M}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}}=\frac{2\pi {{d}_{1}}}{\lambda } \right)$; ${{u}_{2M}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}}=\frac{2\pi {{d}_{2}}}{\lambda } \right)$.

Phương trình sóng tổng hợp tại M là: ${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}$

Độ lệch pha của hai sóng từ hai nguồn đến M là: $\Delta \varphi ={{\varphi }_{2M}}-{{\varphi }_{1M}}=\frac{2\pi }{\lambda }\left( {{d}_{1}}-{{d}_{2}} \right)+{{\varphi }_{2}}-{{\varphi }_{1}}$.

Do đó $A_{M}^{2}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\text{cos}\Delta \varphi $.

TH1: Tại M có biên độ cực đại $\left( {{A}_{M\,\max }} \right)$.

Điều kiện biên độ cực đại: $\Delta \varphi =k2\pi \Leftrightarrow \frac{2\pi }{\lambda }\left( {{d}_{1}}-{{d}_{2}} \right)+{{\varphi }_{2}}+{{\varphi }_{1}}=k2\pi \Leftrightarrow {{d}_{1}}-{{d}_{2}}=\frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{2\pi }+k\lambda $.

Khi đó ${{A}_{M\max }}={{A}_{1}}+{{A}_{2}}$.

TH2: Tại M có biên độ cực tiểu $\left( {{A}_{M\,\min }} \right)$.

Điều kiện biên độ cực tiểu: $\Delta \varphi =k2\pi \Leftrightarrow \frac{2\pi }{\lambda }\left( {{d}_{1}}-{{d}_{2}} \right)+{{\varphi }_{2}}-{{\varphi }_{1}}=\left( 2k+1 \right)\pi $

$\Leftrightarrow {{d}_{1}}-{{d}_{2}}=\frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{2\pi }+\left( k+0,5 \right)\lambda $. Khi đó ${{A}_{M\min }}=\left| {{A}_{1}}-{{A}_{2}} \right|$.

Các trường hợp đặc biệt:

+) Khi ${{A}_{1}}={{A}_{2}}=A$ ta có: $\left\{ \begin{array}{*{35}{l}}{{u}_{1}}=A\cos \left( \omega t+{{\varphi }_{1}} \right) \\{{u}_{2}}=A\cos \left( \omega t+{{\varphi }_{2}} \right) \\\end{array} \right.\Rightarrow \left\{ \begin{array}{*{35}{l}}{{u}_{1M}}=A\cos \left( \omega t+{{\varphi }_{1}}-\frac{2\pi {{d}_{1}}}{\lambda } \right) \\{{u}_{2M}}=A\cos \left( \omega t+{{\varphi }_{2}}-\frac{2\pi {{d}_{2}}}{\lambda } \right) \\\end{array} \right.$.

Sử dụng công thức lượng giác ta có:

${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}=2A\cos \left( \omega t+\frac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2}-\frac{\pi \left( {{d}_{1}}+{{d}_{2}} \right)}{\lambda } \right)\text{cos}\left( \frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{2}+\frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right)$.

Khi đó ${{A}_{M}}=\left| \text{2Acos}\left( \frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{2}+\frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right) \right|$.

+) Khi ${{A}_{1}}={{A}_{2}}=A$ và ${{\varphi }_{1}}={{\varphi }_{2}}$ (hai nguồn dao động cùng pha) ta có:

${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}=2A\cos \left( \omega t+\varphi -\frac{\pi \left( {{d}_{1}}+{{d}_{2}} \right)}{\lambda } \right)\text{cos}\left( \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right)$.

þ Cực đại giao thoa: $\left\{ \begin{array}{*{35}{l}}{{A}_{\text{max}}}=2A \\{{d}_{1}}-{{d}_{2}}=k\lambda \\\end{array} \right.$.

þ Cực tiểu giao thoa: $\left\{ \begin{array}{*{35}{l}}{{A}_{\text{min}}}=0 \\{{d}_{1}}-{{d}_{2}}=\left( k+0,5 \right)\lambda \\\end{array} \right.$.

+) Khi ${{A}_{1}}={{A}_{2}}=A$ và $\left\{ \begin{array}{*{35}{l}}{{\varphi }_{1}}=\varphi \\{{\varphi }_{2}}=\varphi +\pi \\\end{array} \right.$ (hai nguồn dao động ngược pha) ta có:

${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}=2A\cos \left( \omega t+\varphi +\frac{\pi }{2}-\frac{\pi \left( {{d}_{1}}+{{d}_{2}} \right)}{\lambda } \right)\text{cos}\left( \frac{-\pi }{2}+\frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right)$.

þ Cực đại giao thoa: $\left\{ \begin{array}{*{35}{l}}{{A}_{\text{max}}}=0 \\{{d}_{1}}-{{d}_{2}}=\left( k+0,5 \right)\lambda \\\end{array} \right.$.

þ Cực tiểu giao thoa: $\left\{ \begin{array}{*{35}{l}}{{A}_{\text{min}}}=0 \\{{d}_{1}}-{{d}_{2}}=k\lambda \\\end{array} \right.$.