Cách giải các dạng toán tính quãng đường trong dao động cơ phần 2

Dạng 2: Quãng đường lớn nhất, nhỏ nhất
1. ĐẶT VẤN ĐỀ BÀI TOÁN 1
Bài toán 1: Tính quãng đường lớn nhất và nhỏ nhất mà vật đi được khi xét trong cùng khoảng thời gian $\vartriangle t$
2. PHƯƠNG PHÁP GIẢI BÀI TOÁN 1
So sánh khoảng thời gian $\vartriangle t$ mà bài toán cho với nửa chu kỳ $\frac{T}{2}$.
§ TH1: Nếu $0<\vartriangle t<\frac{T}{2}$
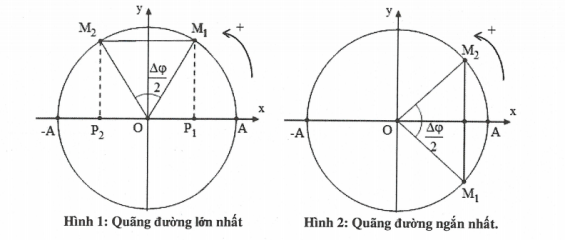
Vật dao động điều hòa có tốc độ càng lớn khi vật càng gần vị trí cân bằng và tốc độ càng nhỏ khi vật càng gần vị trí biên nên xét trong cùng một khoảng thời gian, quãng đường đi được càng dài khi vật ở càng gần vị trí cân bằng và càng ngắn khi vật càng gần vị trí biên. Do có tính đối xứng nên quãng đường dài nhất gồm 2 phần bằng nhau đối xứng qua vị trí cân bằng, còn quãng đường ngắn nhất cũng gồm 2 phần bằng nhau nhưng đối xứng qua vị trí biên.
Sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều.
Ta có: Góc quét $\vartriangle \varphi =\omega \vartriangle t.$
Quãng đường lớn nhất đối xứng qua trục sin khi vật đi từ ${{M}_{1}}\to {{M}_{2}}$(hình 1):
${{S}_{\max }}=2A\sin \frac{\vartriangle \varphi }{2}=2A\sin \frac{\omega .\vartriangle t}{2}.$
Quãng đường ngắn nhất đối xứng nhau qua trục cos khi vật đi từ ${{M}_{1}}\to {{M}_{2}}$(hình 2):
${{S}_{\min }}=2A\left( 1-\cos \frac{\vartriangle \varphi }{2} \right)=2A\left( 1-\cos \frac{\omega .\vartriangle t}{2} \right).$
§ TH2: Nếu $\vartriangle t>\frac{T}{2}.$
Tách $\vartriangle t=n.\frac{T}{2}+\vartriangle {t}'$ ở đó $n\in \mathbb{N}*;0<\vartriangle {t}'<\frac{T}{2}.$
Với khoảng thời gian $n\frac{T}{2}$ thì quãng đường vật đi được là $2nA$.
Trong khoảng thời gian $\vartriangle {t}'=\frac{T}{2}$ thì quãng đường lớn nhất, nhỏ nhất được tính một trong hai cách như trường hợp 1.
1. ĐẶT VẤN ĐỀ BÀI TOÁN 2
þ Bài toán 2: Tính thời gian ngắn nhất và dài nhất khi xét cùng độ dài quãng đường S.
2. PHƯƠNG PHÁP GIẢI
Vật dao động điều hòa có tốc độ càng lớn khi vật càng gần vị trí cân bằng và tốc độ càng nhỏ khi vật càng gần vị trí biên nên trong cũng quãng đường, khoảng thời gian sẽ dài khi vật đi gần vị trí biên. Khoảng thời gian sẽ ngắn khi vật đi xung quanh gần vị trí cân bằng.
§ TH1: Nếu S < 2A ta có:
Thời gian ngắn nhất vật đi được quãng đường S: $S=2A\sin \frac{\vartriangle {{\varphi }_{\min }}}{2}=2A\sin \frac{\omega \vartriangle {{t}_{\min }}}{2}.$
Thời gian dài nhất vật đi được quãng đường S: $S=2A\left( 1-\cos \frac{\vartriangle {{\varphi }_{\max }}}{2} \right)=2A\left( 1-\cos \frac{\omega \vartriangle {{t}_{\max }}}{2} \right).$
§ TH2: Nếu $S>2A\Rightarrow S=n.2A+{S}'\Rightarrow \vartriangle t=n\frac{T}{2}+\vartriangle {t}'\left( {S}'<2A \right).$
Khi đó ta tìm $\vartriangle {{{t}'}_{\min }}$ hoặc $\vartriangle {{{t}'}_{\max }}$như trường hợp 1.
3. BÀI TẬP MINH HỌA DẠNG 1
| Bài tập 1: Một vật dao động điều hòa với biên độ A và chu kì T. Tìm quãng đường lớn nhất và nhỏ nhất mà vật đi được trong các khoảng thời gian sau:
A. $\frac{T}{6}.$ B. $\frac{T}{4}.$ C. $\frac{T}{3}.$ D. $\frac{2T}{3}.$ |
Lời giải chi tiết
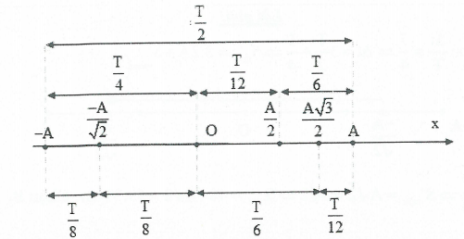
Dựa vào trục thời gian và các khoảng thời gian đặc biệt, ta có:
a) Ta có:
$\frac{T}{6}=\frac{T}{12}+\frac{T}{12}\Rightarrow {{S}_{\max }}=\frac{A}{2}+\frac{A}{2}=A;{{S}_{\min }}=2\left( A-\frac{A\sqrt{3}}{2} \right)$
Hoặc: $\vartriangle t=\frac{T}{6}\Rightarrow \vartriangle \varphi =\frac{2\pi }{T}.\frac{T}{6}=\frac{\pi }{3}\Rightarrow \left\{ \begin{array}{} {{S}_{\max }}=2A\sin \frac{\pi }{6}=A \\ {} {{S}_{\min }}=2A\left( 1-\cos \frac{\pi }{6} \right)=2\left( A-\frac{A\sqrt{3}}{2} \right) \\ \end{array} \right..$
b) Ta có:
$\frac{T}{4}=\frac{T}{8}+\frac{T}{8}\Rightarrow \left\{ \begin{array}{} {{S}_{\max }}=2.\frac{A\sqrt{2}}{2}=A\sqrt{2} \\ {} {{S}_{\min }}=2\left( A-\frac{A\sqrt{2}}{2} \right)=A\left( 2-\sqrt{2} \right) \\ \end{array} \right..$
Hoặc: $\vartriangle t=\frac{T}{8}\Rightarrow \vartriangle \varphi =\frac{2\pi}{T}.\frac{T}{8}=\frac{\pi }{4}\Rightarrow \left\{ \begin{array}{} {{S}_{\max }}=2A\sin \frac{\pi }{4}=A\sqrt{2} \\ {} {{S}_{\min }}=2A\left( 1-\cos \frac{\pi }{4} \right)=\left( A-A\sqrt{2} \right) \\ \end{array} \right..$
c) Ta có:
$\frac{T}{3}=\frac{T}{6}+\frac{T}{6}\Rightarrow \left\{ \begin{array}{} {{S}_{\max }}=2.\frac{A\sqrt{3}}{2}=A\sqrt{3} \\ {} {{S}_{\min }}=2\left( A-\frac{A}{2} \right)=A \\ \end{array} \right..$
d) Trong trường hợp này $\vartriangle t>\frac{T}{2}.$
Ta có:
$\begin{array}{} \frac{2T}{3}=\frac{T}{2}+\frac{T}{6}=\frac{T}{2}+\frac{T}{12}+\frac{T}{12}\Rightarrow {{S}_{\max
}}=2A+{{{{S}'}}_{\max }}=2A+A=3A. \\ {} {{S}_{\min }}=2A+{{{{S}'}}_{\min }}=2A+2\left( A-\frac{A\sqrt{3}}{2} \right)=4A-A\sqrt{3.} \\ \end{array}$
| Bài tập 2: Một vật dao động điều hòa với phương trình $x=8\cos \left( 5\pi t+\frac{\pi }{4} \right)cm$. Quãng đường lớn nhất mà vật đi được trong khoảng thời gian 0,7s là
A. 53,66 cm. B. 59,31 cm. C. 56 cm. D. 61,86 cm. |
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=0,4s;\frac{\vartriangle t}{T}=\frac{7}{4}\Rightarrow \vartriangle t=3\frac{T}{2}+\frac{T}{4}\Rightarrow {{S}_{\max }}=3.2A+{{{S}'}_{\max \left( \frac{T}{4} \right)}}$

Mặt khác $\frac{T}{4}=\frac{T}{8}+\frac{T}{8}\Rightarrow {{{S}'}_{\max }}=A\sqrt{2}=8\sqrt{2}\Rightarrow {{S}_{\max }}=48+8\sqrt{2}=59,31cm.$ Chọn B.
| Bài tập 3: Một vật dao động điều hòa với phương trình $x=10\cos \left( \frac{4\pi t}{3}+\frac{\pi }{4} \right)cm.$Quãng đường ngắn nhất mà vật đi được trong khoảng thời gian $\vartriangle t=11,5s$là
A. 302,7 cm. B. 310 cm. C. 160 cm. D. 152,7 cm. |
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=1,5s;\frac{\vartriangle t}{T}=\frac{23}{3}\Rightarrow \vartriangle t=15\frac{T}{2}+\frac{T}{6}=15.\frac{T}{2}+\frac{T}{12}+\frac{T}{12}.$

Do đó ${{S}_{\max }}=15.2A+{{{S}'}_{\min }}=30A+2A-A\sqrt{3}=302,7cm.$ Chọn A.
| Bài tập 4: Một vật dao động điều hòa với chu kì T và biên độ A. Quãng đường lớn nhất vật đi được trong khoảng thời gian $\frac{5T}{3}$ là
A. 5A. B. 7A. C. 3A. D. 6,5A. |
.
Lời giải chi tiết
Ta có: $\frac{5T}{3}=3\frac{T}{2}+\frac{T}{6}\Rightarrow {{S}_{\max }}=3.2A+{{{S}'}_{\max .}}$

Lại có: $\frac{T}{6}=2.\frac{T}{12}\Rightarrow {{{S}'}_{\max }}=A\Rightarrow {{S}_{\max }}=7A.$ Chọn B.
| Bài tập 5: Một vật dao động điều hòa với biên độ A và tần số góc $\omega $. Thời gian ngắn nhất để vật đi được quãng đường có độ dài $A\sqrt{3}$ là:
A. $\frac{\pi }{6\omega }$ B. $\frac{\pi }{12\omega }$ C. $\frac{1}{6\omega }$ D. $\frac{2\pi }{3\omega }$ |
Lời giải chi tiết
Thời gian ngắn nhất vật thực hiện được quãng đường đó khi vật di chuyển đối xứng qua vị trí cân bằng.
Khi đó: $A\sqrt{3}=\frac{A\sqrt{3}}{2}+\frac{A\sqrt{3}}{2}\Rightarrow \vartriangle {{t}_{\min }}=2.\frac{T}{6}=\frac{T}{3}=\frac{2\pi }{3\omega }.$
Cách 2: Áp dụng công thức: Thời gian ngắn nhất vật đi được quãng đường $S=A\sqrt{3}$thỏa mãn:
$S=2A\sin \frac{\omega \vartriangle {{t}_{\min }}}{2}\Leftrightarrow \vartriangle {{t}_{\min }}=\frac{2}{\omega }.\arcsin \frac{S}{2A}=\frac{2\pi }{3\omega }.$ Chọn D.
| Bài tập 6: Một vật dao động điều hòa với biên độ A và tần số f. Thời gian ngắn nhất để vật đi được quãng đường có độ dài 3A là
A. $\frac{3}{4f}$. B. $\frac{2}{3f}$. C. $\frac{5}{6f}$. D. $\frac{5}{4f}$. |
Lời giải chi tiết
Ta có: $3A=2A+A\Rightarrow \vartriangle {{t}_{\min }}=\frac{T}{2}+\vartriangle {{{t}'}_{\min }}.$
Thời gian ngắn nhất vật thực hiện được quãng đường A khi vật di chuyển đối xứng qua vị trí cân bằng
Ta có: $A=\frac{A}{2}+\frac{A}{2}\Rightarrow \vartriangle {{{t}'}_{\min }}=2\frac{T}{12}=\frac{T}{6}.$
Do đó: $\vartriangle {{t}_{\min }}=\frac{T}{2}+\frac{T}{6}=\frac{2T}{3}=\frac{2}{3f}.$ Chọn B.
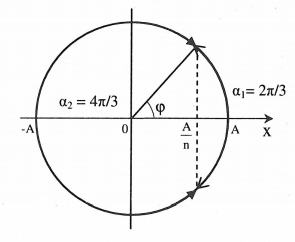
| Bài tập 7: Một vật nhỏ đang dao động điều hòa, biết rằng khoảng thời gian dài nhất giữa hai lần liên tiếp vật đi qua vị trí có li độ bằng A/n đúng bằng khoảng thời gian trong đó vật đi được quãng đường dài nhất là 3A. Giá trị của n là
A. $n=2.$ B. $n=\frac{1}{2}.$ C. $n=\frac{\sqrt{3}}{2}.$ D. $n=\frac{2}{\sqrt{3}}.$ |
Lời giải chi tiết
| ${{S}_{\max }}=k.2A+2A\sin \left( {\alpha }/{2}\; \right)=3A$
$\Rightarrow k=1$ và $\alpha ={\pi }/{3}\;\Rightarrow t=1.\frac{T}{2}+\frac{\alpha }{\omega }=\frac{T}{2}+\frac{T}{6}=\frac{2T}{3}s$( cứ đi được 2A hết T/2 s). Khoảng thời gian đi trong đoạn 3A trên bằng với khoảng thời gian giữa 2 lần liên tiếp đi qua li độ ${A}/{n}\;=t={2T}/{3}\;s.$ $\Rightarrow {{\alpha }_{2}}=\omega .t=\frac{2\pi }{T}.\frac{2T}{3}=\frac{4\pi }{3}rad.$ Quãng thời gian t dài nhất ứng với ${{\alpha }_{2}}$ là cung lớn trên đường tròn. $\Rightarrow $Cung nhỏ ${{\alpha }_{1}}={2\pi }/{3}\;rad.$ $\Rightarrow \varphi ={\pi }/{3}\;\Rightarrow {A}/{n=A.cos{\pi }/{3}\;\Rightarrow n=2}\;.$ Chọn A. |
 |
| Bài tập 8: Một chất điểm khối lượng 200g dao động điều hòa với phương trình $x=10\cos \left( 2\pi t-\frac{2\pi }{3} \right)cm$. Tại thời điểm ${{t}_{1}}$ gia tốc của chất điểm cực tiểu. Tại thời điểm ${{t}_{2}}={{t}_{1}}+\vartriangle t({{t}_{2}}<2015T)$ thì độ lớn động lượng của chất điểm là $0,02\pi \sqrt{2}kgm/s$. Giá trị lớn nhất của $\vartriangle t$ là
A. 2015,825 s. B. 2014,542 s. C. 2014,875 s. D. 2014,625 s. |
Lời giải chi tiết
Chu kì dao động T = 1 s. Ta có $\vartriangle t={{t}_{2}}-{{t}_{1}}$ để $\vartriangle {{t}_{\max }}\Leftrightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}_{\max }}$
Khi $p=0,02\pi \sqrt{2}\Rightarrow v=\frac{p}{m}=10\pi \sqrt{2}cm/s.$
Khi $v=10\pi \sqrt{2}\Rightarrow x=\pm 10\sqrt{2}.$ Trong một chu kì vật đi qua vị trí có vận tốc $10\pi \sqrt{2}cm/s$ 2 lần
Để ${{\left( {{t}_{2}}-{{t}_{1}} \right)}_{\max }}$ thì lúc đó chất điểm phải ở xa vị trí biên dương nhất $\Rightarrow $chính là vị trí có $x=10\sqrt{2}$ và $v>0$
$\Rightarrow $Từ vị trí t1, đến vị trí đó mất khoảng thời gian $t=T-\frac{T}{8}=\frac{7T}{8}=\frac{7}{8}s$
Do$\Rightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}_{\max }}=kT+\frac{7}{8}=2k+\frac{7}{8}.$
Do $\vartriangle t<2015T\Rightarrow 2k+\frac{7}{8}<4030\Leftrightarrow k<2014,5625\Rightarrow k=2014\Rightarrow \vartriangle {{t}_{\max }}=2014,825s.$ Chọn C.
| Bài tập 9: Một chất điểm dao động điều hòa với phương trình $x=A\cos \left( \pi t-\frac{\pi }{6} \right)cm$. Tại thời điểm ${{t}_{1}}$, gia tốc của chất điểm đổi chiều. Tại thời điểm ${{t}_{2}}={{t}_{1}}+\vartriangle t(\vartriangle t<2015T)$ thì tốc độ của chất điểm là $\frac{A\pi }{3}cm/s.$ Giá trị lớn nhất của $\vartriangle t$ là
A. 4029,608 s. B. 4029,892 s. C. 4025,25 s. D. 4025,4 s. |
Lời giải chi tiết
Chu kì dao động T = 2 s. Ta có $\vartriangle t={{t}_{2}}-{{t}_{1}}$ để $\vartriangle {{t}_{\max }}\Leftrightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}_{\max }}$
Khi $v=\frac{A\pi }{3}\Rightarrow x=\sqrt{{{A}^{2}}-{{\left( \frac{v}{\omega } \right)}^{2}}}=\frac{2\sqrt{2}A}{3}$. Trong một chu kì vật đi qua vị trí có tốc độ $\frac{A\pi }{3}cm/s$4 lần.
Để ${{\left( {{t}_{2}}-{{t}_{1}} \right)}_{\max }}$ thì lúc đó chất điểm phải ở xa vị trí biên dương nhất $\Rightarrow $chính là vị trí có $x=10\sqrt{2}$ và $v>0$
Và lúc đó chiều chuyển động là lúc vật đi qua vị trí cân bằng theo chiều âm
$\Rightarrow $ Từ vị trí ${{t}_{1}}$ đến vị trí đó mất khoảng thời gian $t=\frac{T}{2}+\frac{\arcsin \left( \frac{2\sqrt{2}}{3} \right)T}{2\pi }=0,6959T=1,4s$
Do$\Rightarrow \left( {{t}_{2}}-{{t}_{1}} \right)\max =kT+1,4=2k+1,4$
Do $\vartriangle t<2015T\Rightarrow 2k+1,4<4030\Leftrightarrow k<2014,3\Rightarrow k=2014\Rightarrow \vartriangle {{t}_{\max }}=4029,4s.$ Chọn D.
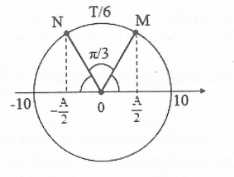
| Bài tập 10: Một vật dao động điều hòa có biên độ A = 10 cm. Trong khoảng thời gian $\frac{13}{6}s$ vật đi được quãng đường lớn nhất S = 90 cm. Tìm tốc độ của vật ở cuối quãng đường trên.
A. $5\sqrt{2}\pi cm/s.$ B. $10\sqrt{2}\pi cm/s.$ C. $10\sqrt{3}\pi cm/s.$ D. $10\pi cm/s.$ |
Lời giải chi tiết
| ${{S}_{\max }}=90cm=9A=2.(4A)+A\Leftrightarrow t=\frac{13}{6}s=2T+\vartriangle t$
$\Rightarrow {{S}_{\max }}\left( \vartriangle t \right)=A$ đối xứng nhau qua vị trí cân bằng, mỗi bên $={A}/{2}\;$$\Rightarrow \widehat{MN}=\frac{\pi }{3}\Rightarrow \vartriangle t=\frac{T}{6}.$ $\begin{array}{} \Rightarrow t=\frac{13}{6}s=2T+\frac{T}{6}=>T=1s \\ {} {{x}_{cuoi}}=\pm \frac{A}{2}\Rightarrow \left| v\right|=\frac{\sqrt{3}}{2}{{v}_{0}}=\frac{\sqrt{3}}{2}.2\pi .10=10\sqrt{3}\pi cm/s. \\ \end{array}$ |
 |
Chọn C.
| Bài tập 11: Một vật dao động điều hòa dọc theo trục Ox, gọi $\vartriangle t$ là khoảng thời gian giữa 2 lần liên tiếp vật có động năng bằng thế năng. Tại thời điểm t vật qua vị trí có tốc độ $15\pi \sqrt{3}cm/s$với độ lớn gia tốc $22,5m/{{s}^{2}}$, sau đó một khoảng thời gian đúng bằng $\vartriangle t$ vật qua vị trí có độ lớn vận tốc $45\pi cm/s$. Lấy ${{\pi }^{2}}=10$. Quãng đường mà vật có thể đi được tối đa trong 0,1s là
A. $6\sqrt{3}cm$ B. $6\sqrt{6}cm$ C. $6\sqrt{2}cm$ D. $6cm$ |
Lời giải chi tiết
Thời gian ngắn nhất giữa 2 lần liên tiếp vật có động năng bằng thế năng: $\vartriangle t=\frac{T}{4}\Rightarrow \vartriangle \varphi =\frac{\pi }{2}.$
Vận tốc tại thời điểm ${{t}_{1}}$ vuông pha với vận tốc tại thời điểm $t={{t}_{1}}+\vartriangle t$ suy ra $x=\frac{A}{2}.$
Áp dụng hệ thức vuông pha tại thời điểm ${{t}_{1}}$ ta có: ${{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}+{{\left( \frac{a}{{{a}_{\max }}} \right)}^{2}}=1\Leftrightarrow {{a}_{\max }}=15\sqrt{3}m/{{s}^{2}}$
$\Rightarrow \omega =\frac{{{a}_{\max }}}{{{v}_{\max }}}=5\pi \Rightarrow A=6\sqrt{3}cm.$
Mặt khác ${{S}_{\max }}=2A\sin \frac{\omega \vartriangle t}{2}=2.6\sqrt{3}.\sin \frac{5\pi .0,1}{2}=6\sqrt{3}cm.$ Chọn A.
VẬT LÝ LỚP 12
