Cho mạch điện như hình vẽ:
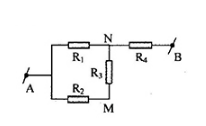
Phương pháp giải
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: \(R{\rm{ }} = {\rm{ }}{R_1} + {\rm{ }}{R_2} + {\rm{ }}....{\rm{ }} + {\rm{ }}{R_n}\)
+ Áp dụng biểu thức xác định điện trở trong mạch song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}\)
Lời giải của Tự Học 365
Vì ampe kế có điện trở rất nhỏ nên M và B cùng điện thế
=> chập M và B mạch điện được vẽ lại như hình
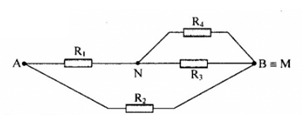
Ta có: \({R_2}//{\rm{ }}[\left( {{R_1}nt{\rm{ }}\left( {{R_3}//{R_4}} \right)} \right]\)
\(\begin{array}{l}\dfrac{1}{{{R_{34}}}} = \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_4}}}\\ \to {R_{34}} = \dfrac{{{R_3}{R_4}}}{{{R_3} + {R_4}}} = \dfrac{{3.6}}{{3 + 6}} = 2\Omega \end{array}\)
\({R_{134}} = {R_1} + {R_{34}} = 3 + 2 = 5\Omega \)
Điện trở tương đương của toàn mạch: \(\dfrac{1}{R} = \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_{134}}}} \to R = \dfrac{{{R_2}{R_{134}}}}{{{R_2} + {R_{134}}}} = \dfrac{{3.5}}{{3 + 5}} = \dfrac{{15}}{8}\Omega \)
Đáp án cần chọn là: b
Vật lý Lớp 12
