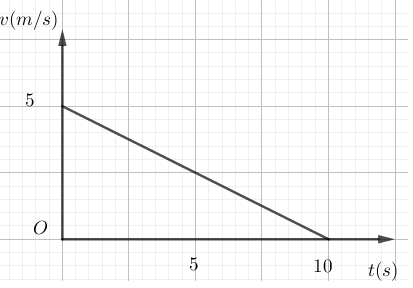
Một xe đạp đang chuyển động với vận tốc \(5m/s\) thì hãm phanh chuyển động chậm dần đều có đồ thị vận tốc theo thời gian như sau:
Phương pháp giải
+ Đọc đồ thị v – t
+ Sử dụng công thức tính gia tốc: \(a = \dfrac{{\Delta v}}{{\Delta t}}\)
+ Sử dụng hệ thức liên hệ: \({v^2} - v_0^2 = 2as\)
Lời giải của Tự Học 365
Từ đồ thị ta có:
+ Vận tốc của xe tại thời điểm \({t_0} = 0\) là \({v_0} = 5m/s\)
+ Vận tốc của xe tại thời điểm \(t = 10s\) là \(v = 0m/s\) (xe dừng lại)
\( \Rightarrow \) Gia tốc của xe: \(a = \dfrac{{\Delta v}}{{\Delta t}} = \dfrac{{v - {v_0}}}{{t - {t_0}}} = \dfrac{{0 - 5}}{{10 - 0}} = - 0,5m/{s^2}\)
Áp dụng công thức liên hệ, ta có:
\({v^2} - v_0^2 = 2as\)
\( \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {5^2}}}{{2.\left( { - 0,5} \right)}} = 25m\)
Đáp án cần chọn là: d
Vật lý Lớp 12
