Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t1, li độ của ba phần tử A, B, C lần lượt là – 2,4mm; 0 mm; 2,4 mm. Nếu tại thời điểm t2, li độ của A và C đều bằng +3,2 mm, thì li độ của phần tử tại B là:
Phương pháp giải
+ Sử dụng vòng tròn lượng giác
+ Sử dụng hệ thức \({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha = 1\)
Lời giải của Tự Học 365
Xác định tọa độ các điểm tại các thời điểm t1 và t2
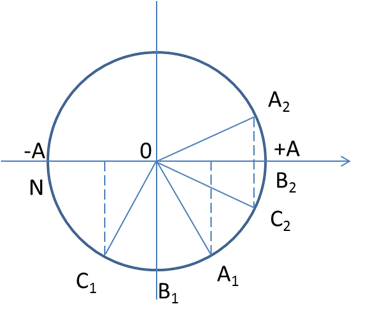
Từ vòng tròn lượng giác, ta có:
B quay góc \({90^0}\)
=> Tại t2 li độ B chính bằng biên độ
A, C cũng tương tự
Ta có:
\(\begin{array}{l}\dfrac{{2,{4^2}}}{{{A^2}}} + \dfrac{{3,{2^2}}}{{{A^2}}} = 1\\ \to A = \sqrt {2,{4^2} + 3,{2^2}} = 4mm\end{array}\)
Đáp án cần chọn là: c
Vật lý Lớp 12
