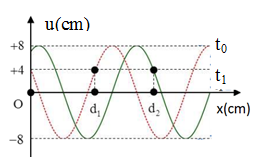
Một sóng cơ truyền trên trục Ox trên một dây đàn hồi rất dài với tần số f = 1/3 Hz. Tại thời điểm t0 = 0 và tại thời điểm t1 = 0,875s hình ảnh của sợi dây được mô tả như hình vẽ. Biết rằng: d2 - d1 = 10 cm. Gọi δ là tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng. Giá trị của δ là:
Phương pháp giải
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính độ lệch pha theo không gian và thời gian:
\(\Delta \varphi = \Delta {\varphi _t} + \Delta {\varphi _x} = \omega \Delta t + \dfrac{{2\pi \Delta x}}{\lambda }\)
Lời giải của Tự Học 365
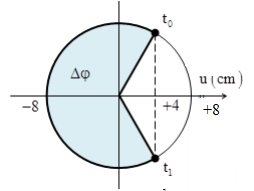
- Biểu diễn trên vòng tròn lượng giác, ta được:
- Độ lệch pha giữa hai điểm cách O các khoảng d1 và d2 như hình vẽ:
\(\begin{array}{l}\Delta \varphi = \Delta {\varphi _t} + \Delta {\varphi _x} = 2\pi f\Delta t + \dfrac{{2\pi \Delta d}}{\lambda } = {240^0} = \dfrac{{4\pi }}{3}\\ \\\leftrightarrow \dfrac{{7\pi }}{{12}} + \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{4\pi }}{3} \\\to \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{3\pi }}{4} \\\to \lambda = \dfrac{{8\Delta d}}{3} = \dfrac{{8.10}}{3} = \dfrac{{80}}{3}cm\end{array}\)
Tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng:
\(\delta = \dfrac{{\omega A}}{v} = \dfrac{{\omega A}}{{\lambda f}} = \dfrac{{\omega A}}{{\lambda \dfrac{\omega }{{2\pi }}}} = \dfrac{{2\pi A}}{\lambda } = \dfrac{{2\pi 8}}{{\dfrac{{80}}{3}}} = \dfrac{{3\pi }}{5}\)
Đáp án cần chọn là: b
Vật lý Lớp 12
