Cho hypebol (H):x^2 4 - y^2 16 = 1. Tìm phương trình đường chéo của hình chữ nhật tâm O có 4 đỉnh

Câu hỏi
Nhận biếtCho hypebol \((H):\,{{{x^2}} \over 4} - {{{y^2}} \over {16}} = 1\). Tìm phương trình đường chéo của hình chữ nhật tâm O có 4 đỉnh thuộc (H) sao cho hệ số góc các đường chéo là số nguyên.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
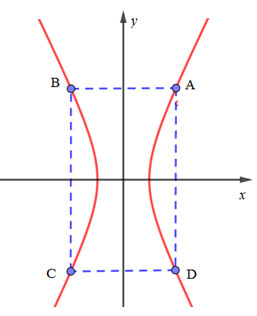
Gọi\(A\left( {{x_0};\,{y_0}} \right),\,\,B\left( { - {x_0};\,{y_0}} \right),\,C\left( { - {x_0};\, - {y_0}} \right);\,D\left( {{x_0};\, - {y_0}} \right),\,\,({x_0},{y_0} > 0)\) là 4 đỉnh của hình chữ nhật ABCD, có tâm O.
\(A,B,C,D \in (H) \Rightarrow {{{x_0}^2} \over 4} - {{{y_0}^2} \over {16}} = 1\) (1)
Phương trình đường thẳng \(AC:\,\,y = {{{y_0}} \over {{x_0}}}x\) và phương trình đường thẳng \(BD:\,\,y = - {{{y_0}} \over {{x_0}}}.x\)
Hệ số góc của đường chéo AC, BD lần lượt là : \({{{y_0}} \over {{x_0}}}\) và \( - {{{y_0}} \over {{x_0}}}\)
Hệ số góc các đường chéo là số nguyên \( \Leftrightarrow {{{y_0}} \over {{x_0}}} \in Z,\, - {{{y_0}} \over {{x_0}}} \in Z \Leftrightarrow {{{y_0}} \over {{x_0}}} \in Z.\)
Đặt \({{{y_0}} \over {{x_0}}} = k \in {Z^ + } \Leftrightarrow {y_0} = k{x_0}\). Thay vào (1), ta được :
\({{{x_0}^2} \over 4} - {{{k^2}{x_0}^2} \over {16}} = 1 \Leftrightarrow {{{k^2}{x_0}^2} \over {16}} = {{{x_0}^2} \over 4} - 1 \Leftrightarrow {k^2}{x_0}^2 = 4{x_0}^2 - 16 \Leftrightarrow {k^2} = 4 - {{16} \over {{x_0}^2}}\) (2)
Từ (2) \( \Rightarrow 0 < {k^2} < 4\)
Mà \(k \in Z \Rightarrow {k^2} = 1 \Leftrightarrow \left[ \matrix{ k = 1\,\,(TM) \hfill \cr k = - 1(L) \hfill \cr} \right.\)
\(k = 1 \Rightarrow AC:\,\,y = x,\,\,\,BD:\,\,y = - x\)
Vậy, phương trình đường chéo cần tìm là: \(y = x,\,\,\,y = - x\).
Chọn: C
