Cho hypebol (H):x^2 a^2 - y^2 b^2 = 1. Lập công thức tính góc varphi tạo bởi 2 đường tiệm cận của

Câu hỏi
Nhận biếtCho hypebol \((H):\,{{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1\). Lập công thức tính góc \(\varphi \) tạo bởi 2 đường tiệm cận của (H).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
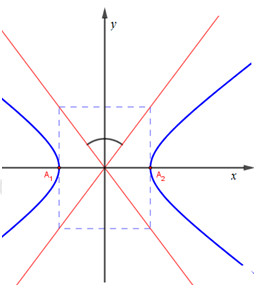
Hypebol \((H):\,{{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1\) có 2 đường tiệm cận là: \(y = {b \over a}x,\,\,\,y = - {b \over a}x\)
Nhận \(\overrightarrow {{n_1}} \left( {b; - a} \right),\,\,\overrightarrow {{n_2}} \left( {b;a} \right)\) lần lượt là các VTPT.
Khi đó, góc tạo bởi 2 đường tiệm cận của (H) được tính bởi công thức: \(\cos \varphi = {{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|} \over {\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = {{\left| {b.b + ( - a).a} \right|} \over {\sqrt {{a^2} + {{\left( { - b} \right)}^2}} .\sqrt {{a^2} + {b^2}} }} = {{\left| {{b^2} - {a^2}} \right|} \over {{a^2} + {b^2}}}\)
Chọn: A.
