Trong mặt phẳng với hệ tọa độ Oxy cho hình chữ nhật ABCD. Các đường thẳng AC và AD lần lượt có phươn

Câu hỏi
Nhận biếtTrong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD. Các đường thẳng AC và AD lần lượt có phương trình là \(x + 3y = 0\) và\( x – y + 4 = 0\), đường thẳng BD đi qua điểm \(M\left( { - \frac{1}{3};1} \right)\). Tính diện tích hình chữ nhật ABCD.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
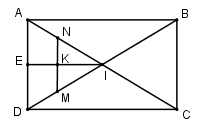
\(A = AC \cap AD \Rightarrow \) Tọa độ của điểm A là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 3y = 0\\x - y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = 1\end{array} \right. \Leftrightarrow A\left( { - 3;1} \right)\)
Kẻ MN // AD \(\left( {N \in AC} \right) \Rightarrow \) phương trình MN có dạng \(x – y + c = 0\).
\(M \in MN \Rightarrow - \frac{1}{3} - 1 + c = 0 \Leftrightarrow c = \frac{4}{3} \Rightarrow pt\left( {MN} \right):x - y + \frac{4}{3} = 0 \Leftrightarrow 3x - 3y + 4 = 0\)
\(N = AC \cap MN \Rightarrow \) Tọa độ điểm N là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 3y = 0\\3x - 3y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = \frac{1}{3}\end{array} \right. \Rightarrow N\left( { - 1;\frac{1}{3}} \right)\)
Gọi K là trung điểm của MN \( \Rightarrow \left\{ \begin{array}{l}{x_K} = \frac{{{x_M} + {x_N}}}{2} = \frac{{ - \frac{1}{3} - 1}}{2} = - \frac{4}{6}\\{y_K} = \frac{{{y_M} + {y_N}}}{2} = \frac{{1 + \frac{1}{3}}}{2} = \frac{4}{6}\end{array} \right. \Leftrightarrow K\left( { - \frac{4}{6};\frac{4}{6}} \right)\)
Gọi I là tâm hình chữ nhật ABCD, kẻ \(IE \bot AD \Rightarrow K \in IE\)
IE vuông góc với AD nên pt(IE) có dạng \(x + y + c = 0.\)
\(K \in IE \Rightarrow - \frac{4}{6} + \frac{4}{6} + c = 0 \Leftrightarrow c = 0 \Rightarrow pt\left( {IE} \right):x + y = 0\)
\(E = IE \cap AD \Rightarrow \) tọa độ điểm E là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 0\\x - y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 2\end{array} \right. \Rightarrow E\left( { - 2;2} \right)\) là trung điểm của AD \( \Rightarrow \left\{ \begin{array}{l}{x_D} = 2{x_E} - {x_A} = - 1\\{y_D} = 2{y_E} - {y_A} = 3\end{array} \right. \Rightarrow D\left( { - 1;3} \right) \Rightarrow AD = \sqrt {{{\left( { - 1 + 3} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = 2\sqrt 2 \)
\(I = AC \cap IE \Rightarrow \) Tọa độ của I là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 0\\x + 3y = 0\end{array} \right. \Leftrightarrow x = y = 0 \Rightarrow I\left( {0;0} \right)\) là trung điểm của AC \( \Rightarrow \left\{ \begin{array}{l}{x_C} = 2{x_I} - {x_A} = 3\\{y_C} = 2{y_I} - {y_A} = - 1\end{array} \right. \Leftrightarrow C\left( {3; - 1} \right) \Rightarrow AC = \sqrt {{{\left( {3 + 3} \right)}^2} + {{\left( { - 1 - 1} \right)}^2}} = 2\sqrt {10} \)
\(\begin{array}{l}\Rightarrow CD = \sqrt {A{C^2} - A{D^2}} = \sqrt {40 - 8} = 4\sqrt 2 \\{S_{ABCD}} = AD.CD = 2\sqrt 2 .4\sqrt 2 = 16\end{array}\)
Chọn B.
