Tam giác ABC nội tiếp đường tròn ( O ) biết góc góc C = 45^o và AB = a. Bán kính đường tròn ( O )

Câu hỏi
Nhận biếtTam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) biết góc \(\widehat C = {45^o}\) và \(AB = a\). Bán kính đường tròn \(\left( O \right)\) là:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Lời giải chi tiết
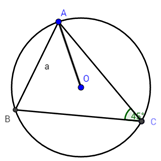
Ta có: \(\widehat {ACB} = {45^0} \Rightarrow \widehat {AOB} = {90^0} \Rightarrow \Delta AOB\) vuông cân tại \(O\).
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\2A{O^2} = A{B^2}\\AO = \frac{{a\sqrt 2 }}{2}\end{array}\)
Chọn đáp án C.

