Hai tập con của R là A và B. Hãy xác định A cup CRB;CRA cap B;CR( A cup B ) và biểu diễn chúng trên

Câu hỏi
Nhận biếtHai tập con của R là A và B. Hãy xác định \(A \cup {C_R}B;{C_R}A \cap B;{C_R}\left( {A \cup B} \right)\) và biểu diễn chúng trên trục số
a) \( A = \left( { - 1;0} \right];B = \left[ {0;2} \right) \)
b) \(A = \left[ {0;3} \right);B = \left( { - 1; + \infty } \right) \)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a) Ta có: \( {C_R}A = \left( { - \infty ; - 1} \right] \cup \left( {0; + \infty } \right)\)
\({C_R}B = \left( { - \infty ;0} \right) \cup \left[ {2; + \infty } \right) \)
\( A \cup B = \left( { - 1;2} \right) \)
Ta có: \(A \cup {C_R}B = \left( { - 1;0} \right] \cup \left( { - \infty ;0} \right) \cup \left[ {2; + \infty } \right) = \left( { - \infty ;0} \right] \cup \left[ {2; + \infty } \right) \)

Ta có: \( {C_R}A \cap B = \left( { - \infty ; - 1} \right] \cup \left( {0; + \infty } \right) \cap \left[ {0;2} \right) = \left( {0;2} \right) \)

Ta có: \( {C_R}\left( {A \cup B} \right) = R\backslash \left( { - 1;2} \right) = \left( { - \infty ; - 1} \right] \cup \left[ {2; + \infty } \right)\)

b) \( A = \left[ {0;3} \right);B = \left( { - 1; + \infty } \right)\)
\({C_R}A = \left( { - \infty ;0} \right) \cup \left[ {3; + \infty } \right)\)
\( {C_R}B = \left( { - \infty ; - 1} \right] \)
\( A \cup B = \left( { - 1; + \infty } \right) \)
Ta có: \( A \cup {C_R}B = \left( { - \infty ; - 1} \right] \cup \left[ {0;3} \right)\)
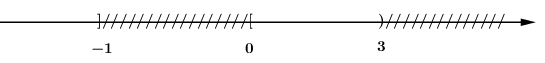
Ta có: \( {C_R}A \cap B = \left( { - \infty ;0} \right) \cup \left[ {3; + \infty } \right) \cap \left( { - 1; + \infty } \right) = \left( { - 1;0} \right) \cup \left[ {3; + \infty } \right) \)
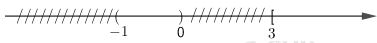
Ta có: \( {C_R}\left( {A \cup B} \right) = R\backslash \left( { - 1; + \infty } \right) = \left( { - \infty ; - 1} \right] \)

Chọn D.
