Đặt AP = x. Tính MP theo R và x. Tìm vị trí của M trên (O) để hình chữ nhật APMQ có diện tích lớn nh

Câu hỏi
Nhận biếtĐặt AP = x. Tính MP theo R và x. Tìm vị trí của M trên (O) để hình chữ nhật APMQ có diện tích lớn nhật.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
AB = 2R, AP = x =>PB = 2R – x
∆AMB vuông tại M có MP là đường cao
=> MP2 = PA.PB = x(2R – x) => MP = 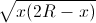
SAPMQ = AP.MP
= x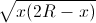 = x√3
= x√3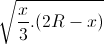 ≤ x√3(
≤ x√3(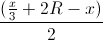
= x√3(R - 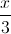 ) = 3√3.
) = 3√3.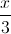 (R -
(R - 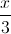 ) ≤ 3√3(
) ≤ 3√3(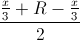 )2 =
)2 = 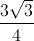 R2
R2
Dấu “ =” xảy ra khi x = 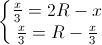 => x =
=> x = 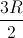
Vậy diện tích MPAQ lớn nhất khi M thuộc đường tròn sao cho P là trung điểm của OB.

