Cho a b c là các số thực dương. Chứng minh rằng nếu <
Câu hỏi
Nhận biếtCho a, b, c là các số thực dương. Chứng minh rằng nếu 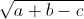= √a + √b - √c thì (a + b – c)2 = a2 + b2 – c2. Điều ngược lại có đúng không? Tại sao?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
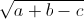= √a + √b - √c => 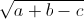+ √c = √a + √b
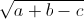=> ( + √c)2 = (√a + √b)2
=> a + b – c + c + 2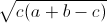
= a + b + 2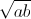
=> =
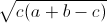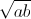
=> c(a + b – c) = ab => c(a + b – c) – ab = 0
=> ca + c(b – c) – ab = 0
=> c(b – c) – a(b – c) = 0
=> c(a + b – c) – ab = 0
=> c(b – c) – a(b – c) = 0
=> (b – c)(c – a) = 0
=> 
=> 
=> 
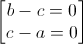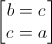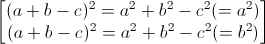
Vậy (a + b – c)2 = a2 + b2 – c2
Điều ngược lại cũng đúng. Thật vậy (a + b – c)2 = a2 + b2 – c2
=> a2 + b2 + c2 + 2ab – 2ca – 2bc = 0 => bc – c2 – ab + ca = 0
=> c(b – c) – a(b – c) = 0
=> (b – c)(c – a) = 0
=> =>
=> 
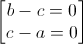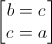
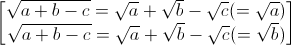
Vậy 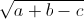= √a + √b - √c.
