[LỜI GIẢI] Cho hình bình hành ABCD, tâm O, M là điểm tùy ý. a. Chứng minh rằng:  - Tự Học 365
KHỞI ĐỘNG CHO MÙA THI ĐẠI HỌC 2026

Ôn đúng trọng tâm – Học chắc từ hôm nay

BẮT ĐẦU NGAY

Cho hình bình hành ABCD, tâm O, M là điểm tùy ý. a. Chứng minh rằng: 

Câu hỏi

Nhận biết

Cho hình bình hành ABCD, tâm O, M là điểm tùy ý.

a. Chứng minh rằng: 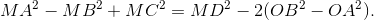MA^{2} - MB^{2}+ MC^{2}= MD^{2} - 2(OB^{2} - OA^{2}).

b. Giả sử M di động trên đường tròn (d), xác định vị trí của M để:

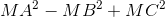MA^{2} - MB^{2}+ MC^{2} đạt giá trị nhỏ nhất.


Đáp án đúng:

Lời giải của Tự Học 365

Giải chi tiết:

a. Ta có: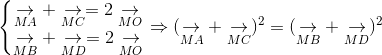 

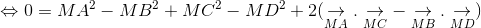 (1)

Ta xét: 

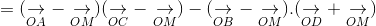
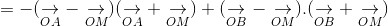
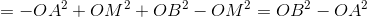           (2)

Thay (2) vào (1), ta được:

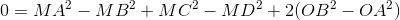
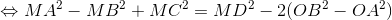, đpcm.

b. Từ kết quả câu a suy ra 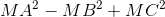 đạt giá trị nhỏ nhất khi và chỉ khi  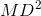nhỏ nhất.

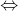 M là hình chiếu vuông góc của D lên (d)

Ý kiến của bạn

Luyện tập

Câu hỏi liên quan

  • Giải Bất phương trình sau : 2x(3x-5) > 0

    Giải Bất phương trình sau :

    2x(3x-5) > 0

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx + m + 3 ≥ 0 với x ε R 

    Định m để  f(x) = mx2 – mx + m + 3 ≥ 0 với x ε R 

    Chi tiết
  • Định m để f(x) = mx<sup>2</sup> – 2(m+1)x – m + 5 > 0 với x

    Định m để f(x) = mx2 – 2(m+1)x – m + 5 > 0 với x < 1

    Chi tiết
  • Định m sao cho : (m+1)x<sup>2</sup> – 2(m+1)x + 4 > 0 ; x ε

    Định m sao cho : (m+1)x2 – 2(m+1)x + 4 > 0 ; x ε R  (1)

    Chi tiết
  • TÌm a để 3 đường thẳng sau đây đồng qui: y=2x ; y= -x-3 ; y

    TÌm a để 3 đường thẳng sau đây đồng qui:

    y=2x ; y= -x-3 ; y= ax + 5

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx – 5 < 0 với x ε R   (1

    Định m để  f(x) = mx2 – mx – 5 < 0 với x ε R   (1)

    Chi tiết
  • Định m sao cho : x<sup>2</sup> – (3m – 2)x + 2m<sup>2</sup>

    Định m sao cho : x2 – (3m – 2)x + 2m2 – 5m – 2 > 0 ; x ε R

    Chi tiết
  • Khảo sát và vẽ đồ thị của hàm số :  1)y = 2|x| 2) y = 3√x

    Khảo sát và vẽ đồ thị của hàm số : 

    1)y = 2|x|

    2) y = 3√x

    Chi tiết
  • Định m để f(x) = x<sup>2</sup> – 2mx – m ≥ 0 với x > 0     

    Định m để f(x) = x2 – 2mx – m ≥ 0 với x > 0           

    Chi tiết
  • Định m sao cho : mx<sup>2</sup> – 10x – 5 ≤ 0 ; x ε R  (1)

    Định m sao cho : mx2 – 10x – 5 ≤ 0 ; x ε R  (1)

    Chi tiết