Cho tam giác ABC có widehatBAC=60^0;AC=b,AB=c (b>c). Đường kính EF củ

Câu hỏi
Nhận biếtCho tam giác ABC có \(\widehat{BAC}={{60}^{0}};AC=b,AB=c\ \ (b>c).\) Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H, K là chân đường vuông góc hạ từ F xuống các đường AB và AC.
a) Chứng minh các tứ giác AEIJ và CMJE nội tiếp và EA.EM = EC. EI.
b) Chứng minh I, J, M thẳng hàng và IJ vuông góc với HK.
c) Tính độ dài cạnh BC và bán kính đường tròn ngoại tiếp tam giác ABC theo b, c.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
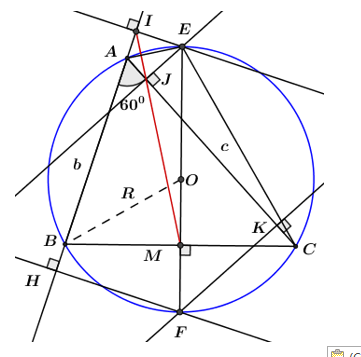
a)
Vì \(\widehat{AIE}+\widehat{\text{AJ}E}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow \) tứ giác AIEJ nội tiếp.
Vì \(\widehat{CJE}=\widehat{CME}={{90}^{0}}\Rightarrow \)tứ giác CMJE nội tiếp (hai góc
cùng nhìn cạnh EC).
Vì \(\widehat{IAE}={{180}^{0}}-\widehat{BAE}=\widehat{BCE}=\widehat{MCE}\) (góc ngoài của tứ
giác nội tiếp).
Và \(\widehat{AIE}=\widehat{CME}={{90}^{0}}.\)
\(\begin{align} \Rightarrow \Delta AIE\sim \Delta CME(g.g) \\ \Rightarrow \frac{EA}{EC}=\frac{EI}{EM}\Rightarrow EA.EM=EI.EC\left( dpcm \right). \\ \end{align}\)
b) Tứ giác IEMB có: \(\widehat{BIE}+\widehat{EMB}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\)
\(\Rightarrow \)Tứ giác IEMB nội tiếp \(\Rightarrow \widehat{IEM}+\widehat{MBI}={{180}^{0}}.\) (tổng hai góc
đối diện)
Do tứ giác ABCE nội tiếp nên: \(\widehat{AEC}+\widehat{CBA}={{180}^{0}}\Rightarrow \widehat{IEM}=\widehat{AEC}\) (cùng bù với góc ABC).
\(\begin{align} \Rightarrow \widehat{IEA}+\widehat{AEM}=\widehat{AEM}+\widehat{MEC} \\ \Rightarrow \widehat{IEA}=\widehat{MEC}. \\ \end{align}\)
Mà tứ giác IEJA nội tiếp nên: \(\widehat{IEA}=\widehat{\text{IJ}A}\) (cùng nhìn đoạn IA).
Tứ giác EJMC nội tiếp nên: \(\widehat{MEC}=\widehat{MJC}\Rightarrow \widehat{\text{IJ}A}=\widehat{MJC}\)
Lại có A, J, C thẳng hàng nên I, J, M thẳng hàng.
Tương tự có M, H, K thẳng hàng.
Xét tam giác EFC có EF là đường kính hình tròn ngoại tiếp tam giác do đó:
\(\widehat{ECF}={{90}^{0}}\Rightarrow \widehat{\text{ECJ}}+\widehat{JCF}={{90}^{0}}\)
Mặt khác:
\(\begin{align} \widehat{\text{ACJ}}+\widehat{KFC}={{90}^{0}}\Rightarrow \widehat{\text{ECJ}}=\widehat{KFC} \\ \Rightarrow \widehat{JME}=\widehat{KMC} \\ \widehat{EMK}+\widehat{KMC}=\widehat{EMC}={{90}^{0}} \\ \Rightarrow \widehat{EMK}+\widehat{JME}=\widehat{JMK}={{90}^{0}} \\ \Rightarrow IK\bot HK\left( dpcm \right). \\ \end{align}\)
c) Áp dụng định lý cos và sin trong tam giác ta thu được:
\(\begin{align} B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB.AC-\sin \widehat{BAC} \\ \Rightarrow B{{C}^{2}}={{b}^{2}}+{{c}^{2}}-bc\sqrt{3} \\ \end{align}\)
Theo định lý sin ta lại có:
\(\frac{BC}{\sin \widehat{BAC}}=2R\Rightarrow R=\frac{\sqrt{{{b}^{2}}+{{c}^{2}}-bc\sqrt{3}}}{\sqrt{3}}\)

