1) Cho tứ giác ABCD, chứng minh: rightarrow AB + rightarrow CD = ri

Câu hỏi
Nhận biết1) Cho tứ giác \(ABCD,\) chứng minh: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} .\)
2) Trong mặt phẳng \(Oxy\), cho các vectơ \(\overrightarrow a \left( {2; - 1} \right),\overrightarrow b \left( {0;4} \right),\overrightarrow c \left( {3;3} \right).\) Tìm hai số thực \(m,n\) sao cho \(\overrightarrow c = m\overrightarrow a - n\overrightarrow b .\)
3) Cho tam giác \(ABC,\) gọi \(I,\,\,J\) lần lượt là trung điểm các cạnh \(AB\) và \(AC.\) Điểm \(M\) nằm trên cạnh \(BC\) sao cho \(MC = 2MB.\) Hãy phân tích vectơ \(\overrightarrow {AM} \) theo hai vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} .\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) Cho tứ giác \(ABCD,\) chứng minh: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} .\)
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \Leftrightarrow \left( {\overrightarrow {AB} - \overrightarrow {AD} } \right) + \left( {\overrightarrow {CD} - \overrightarrow {CB} } \right) = 0 \Leftrightarrow \overrightarrow {DB} + \overrightarrow {BD} = 0\), luôn đúng.
Vậy ta có điều phải chứng minh.
2) Trong mặt phẳng \(Oxy,\) cho các vecto \(\overrightarrow a \left( {2; - 1} \right),\,\,\overrightarrow b \left( {0;\,\,4} \right),\,\,\overrightarrow c \left( {3;\,\,3} \right).\) Tìm hai số thực \(m,\,\,n\) sao cho \(\overrightarrow c = m\overrightarrow a - n\overrightarrow b .\)
Ta có:\(\) \(\left\{ \begin{array}{l}m\overrightarrow a = \left( {2m; - m} \right)\\n\overrightarrow b = \left( {0;4n} \right)\end{array} \right. \Rightarrow m\overrightarrow a - n\overrightarrow b = \left( {2m; - m - 4n} \right).\)
\( \Rightarrow \overrightarrow c = m\overrightarrow a - n\overrightarrow b \Rightarrow \left\{ \begin{array}{l}3 = 2m\\3 = - m - 4n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \frac{3}{2}\\n = \frac{{ - 9}}{8}\end{array} \right..\)
Vậy \(m = \frac{3}{2};\,\,n = \frac{{ - 9}}{8}.\)
3) Cho tam giác \(ABC,\,\) gọi \(I,\,\,J\) lần lượt là trung điểm các cạnh \(AB\) và \(AC.\) Điểm \(M\) nằm trên cạnh \(BC\) sao cho \(MC = 2MB.\) Hãy phân tích vecto \(\overrightarrow {AM} \) theo hai vecto \(\overrightarrow {AI} ,\,\,\overrightarrow {AJ} .\)
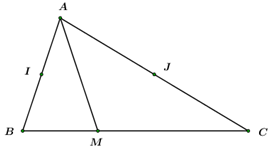
\(\begin{array}{l}\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{1}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\\ = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} = \frac{4}{3}\overrightarrow {AI} + \frac{2}{3}\overrightarrow {AJ} .\end{array}\)
