Cho đường tròn tâm O đường kính MN và dây cung PQ vuông góc với MN tại

Câu hỏi
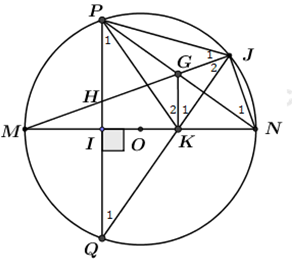
Nhận biếtCho đường tròn tâm O đường kính MN và dây cung PQ vuông góc với MN tại I (I khác M, I khác N). Trên cung nhỏ NP lấy điểm J (J khác N, J khác P), nối M với J cắt PQ tại H. Gọi giao điểm của PN với MJ là G, giao điểm của JQ với MN là K. Chứng minh rằng:
1) Tứ giác GKNJ là tứ giác nội tiếp.
2) KG song song với PQ.
3) Điểm G là tâm đường tròn nội tiếp tam giác PKJ.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) Tứ giác GKNJ là tứ giác nội tiếp.
\(MN\bot PQ\) tại I nên I là trung điểm của \(PQ\) (quan hệ vuông góc giữa đường kính và dây cung)
\(\Rightarrow MN\) là trung trực của PQ.
\(\Rightarrow MP=MQ\Rightarrow sd\overset\frown{MP}=sd\overset\frown{MQ}.\)
Lại có \(\widehat{PNM}\) là góc nội tiếp chắn cung PM, \(\widehat{MJQ}\) là góc nội tiếp chắn cung MQ \(\Rightarrow \widehat{PNM}=\widehat{MJQ}\).
\(\Rightarrow \) Tứ giác GKNJ là tứ giác nội tiếp (Tứ giác có 2 góc nội tiếp cùng chắn 1 cung bằng nhau).
2) KG song song với PQ.
Tứ giác GKNJ nội tiếp \(\Rightarrow \widehat{GKN}+\widehat{GJN}={{180}^{0}}.\)(tổng hai góc đối diện trong tứ giác).
Mà \(\widehat{MJN}\) là góc nội tiếp chắn nửa đường tròn (O) \(\Rightarrow \widehat{MJN}={{90}^{0}}\) (số đo góc nội tiếp bằng nửa số đo cung bị chắn) hay \(GK\bot MN.\)
Lại có \(MN\bot PQ\ \ \left( gt \right)\Rightarrow GK//PQ\) (từ vuông góc đến song song).
3) Điểm G là tâm đường tròn nội tiếp tam giác PKJ.
\(sd\overset\frown{MP}=sd\overset\frown{MQ}\Rightarrow \widehat{{{J}_{1}}}=\widehat{{{J}_{2}}}\Rightarrow \) JG là tia phân giác của \(\widehat{PJK}\)
Ta có : \(K\in MN\Rightarrow KP=KQ\Rightarrow \Delta KPQ\) cân tại K \(\Rightarrow \widehat{{{P}_{1}}}=\widehat{{{Q}_{1}}}\)
Mà \(\widehat{{{P}_{1}}}=\widehat{{{K}_{2}}}\) (so le trong), \(\widehat{{{Q}_{1}}}=\widehat{{{K}_{1}}}\,\,\left( cmt \right)\Rightarrow \widehat{{{K}_{1}}}=\widehat{{{K}_{2}}}\Rightarrow KG\) là tia phân giác của \(\widehat{JKP}\).
\(IG\cap KG=G\Rightarrow \) G là tâm đường tròn nội tiếp tam giác PKJ (đpcm).

