Cho tam giác ABC nội tiếp đường tròn ( O ) đường kính AC( BA < BC ). T

Câu hỏi
Nhận biếtCho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AC\,\,\,\left( {BA < BC} \right).\) Trên đoạn thẳng \(OC\) lấy điểm \(I\) bất kì \(\left( {I \ne C} \right).\) Đường thẳng \(BI\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(D.\) Kẻ \(CH\) \(CH \bot BD\,\,\,\left( {H \in D} \right),\,\,DK \bot AC\,\,\left( {K \in AC} \right).\)
a) Chứng minh rằng tứ giác \(DHKC\) là tứ giác nội tiếp.
b) Cho độ dài đoạn thẳng \(AC\) là \(4cm\) và \(\angle ABD = {60^0}.\) Tính diện tích \(\Delta ACD.\)
c) Đường thẳng đi qua \(K\) song song với \(BC\) cắt đường thẳng \(BD\) tại \(E.\) Chứng minh rằng khi \(I\) thay đổi trên đoạn thẳng \(OC\,\,\left( {I \ne C} \right)\) thì điểm \(E\) luôn thuộc một đường tròn cố đinh.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
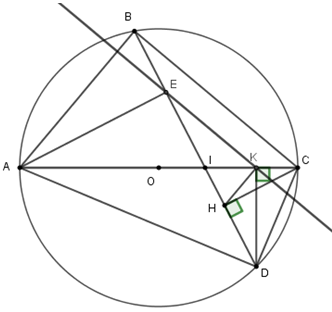
a) Xét tứ giác \(DHKC\) có
\(\angle DHC = 90^\circ \,\)(do \(CH \bot BD\))
\(\angle DKC = 90^\circ \) (do \(DK \bot AC\))
Suy ra \(\angle DHC = \angle DKC\left( { = 90^\circ } \right)\) nên hai đỉnh \(H;K\) kề nhau cùng nhìn cạnh \(CD\) dưới các góc vuông nên tứ giác \(DHKC\) là tứ giác nội tiếp.
b) Gọi \(O\) là trung điểm \(AC\)
Xét đường tròn \(\left( O \right)\) có \(\angle ABD = 60^\circ \Rightarrow \angle ACD = \angle ABD = 60^\circ \) (hai góc nội tiếp cùng chắn cung \(AD\))
Lại có \(\angle CDA = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACD\) vuông tại \(D\) có \(AC = 4cm;\,\angle ACD = 60^\circ \) nên \(AD = AC.\sin \angle ACD = 4.\sin 60^\circ = 2\sqrt 3 \,cm\)
Và \(CD = AC.\cos \angle ACD = 4.\cos 60^\circ = 2\,cm\)
Diện tích tam giác \(ACD\) là \({S_{\Delta ACD}} = \frac{1}{2}AD.DC = \frac{1}{2}.2\sqrt 3 .2 = 2\sqrt 3 \,c{m^2}.\)
c) Vì \(EK//BC \Rightarrow \angle DEK = \angle DBC\) (1) (hai góc ở vị trí đồng vị)
Xét đường tròn \(\left( O \right)\) có \(\angle DBC = \angle DAC\) (2) (hai góc nội tiếp cùng chắn cung \(CD\))
Từ (1) và (2) suy ra \(\angle DEK = \angle DAK\)
Suy ra tứ giác \(AEKD\) có hai đỉnh \(A,E\) cùng nhìn cạnh \(KD\) dưới các góc bằng nhau nên tứ giác \(AEKD\) là tứ giác nội tiếp, suy ra \(\angle AED = \angle AKD = 90^\circ \)
Do đó \(AE \bot EB\) suy ra \(\Delta AEB\) vuông tại \(E.\)
Lại có \(AB\) cố định nên \(E\) thuộc đường tròn đường kính \(AB\) cố định khi \(I\) thay đổi trên đoạn \(OC.\)

