Cho đường tròn ( O ) đường kính AB, trên đường tròn ( O ) lấy điểm M k

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) đường kính \(AB,\) trên đường tròn \(\left( O \right)\) lấy điểm \(M\) không trùng với \(A\) hoặc \(B.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) và \(M\) cắt nhau tại điểm \(C.\)
a) Chứng minh tứ giác \(OACM\) nội tiếp.
b) Chứng minh \(MA.MO = MB.MC.\)
c) Gọi \(D\) là giao điểm của \(AC\) và \(BM.\) Chứng minh \(AC = CD.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
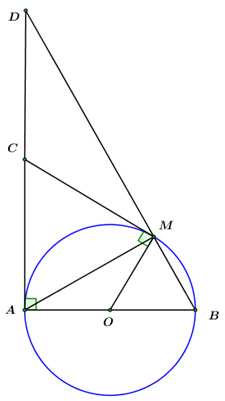
a) Chứng minh tứ giác \(OACM\) nội tiếp.
Ta có: \(CM\) là tiếp tuyến của \(\left( O \right)\) tại\(M \Rightarrow OM \bot MC \Rightarrow \angle OMC = {90^0}.\)
\(AC\) là tiếp tuyến của \(\left( O \right)\) tại \(A \Rightarrow OA \bot CA \Rightarrow \angle OAC = {90^0}.\)
Xét tứ giác \(OACM\) ta có: \(\angle CAO + \angle OMC = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện.
\( \Rightarrow OACM\) là tứ giác nội tiếp. (dhnb)
b) Chứng minh \(MA.MO = MB.MC.\)
Ta có: \(\angle AMC = \angle ABM\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AM\))
Xét \(\Delta OMB\) ta có: \(OM = OB = R \Rightarrow \Delta OMB\) là tam giác cân tại \(O.\)
\( \Rightarrow \angle OMB = \angle OBM.\) (tính chất tam giác cân)
Xét \(\Delta CAM\) ta có: \(CA = CM\) (tính chất hai đường tiếp tuyến cắt nhau).
\( \Rightarrow \Delta CAM\) là tam giác cân tại \(C.\)
\( \Rightarrow \angle CAM = \angle CMA.\) (tính chất tam giác cân)
\(\begin{array}{l} \Rightarrow \angle OMB = \angle MBO = \angle CMA = \angle CAM.\\ \Rightarrow \Delta CAM \sim \Delta OBM\,\,\left( {g - g} \right)\\ \Rightarrow \frac{{MA}}{{MB}} = \frac{{MC}}{{MO}} \Leftrightarrow MA.MO = MB.MC\,\,\,\left( {dpcm} \right).\end{array}\)
c) Gọi \(D\) là giao điểm của \(AC\) và \(BM.\) Chứng minh \(AC = CD.\)
Ta có: \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( O \right)\))
\( \Rightarrow AM \bot BM\,\,hay\,\,\,AM \bot BD \Rightarrow \angle AMD = {90^0}\)
\( \Rightarrow \Delta AMD\) là tam giác vuông tại \(M.\)
\( \Rightarrow \left\{ \begin{array}{l}\angle ADM + \angle DAM = {90^0}\\\angle CMA + \angle CMD = {90^0}\end{array} \right.\)
Mà \(\angle CAM = \angle CMA\,\,\,\left( {cm\,\,b} \right)\)
\( \Rightarrow \angle ADM = \angle DMC\,\,\,hay\,\,\,\angle CDM = CMD\)
\( \Rightarrow \Delta CMD\) là tam giác cân tại \(C \Rightarrow CD = CM\)
Mặt khác: \(CA = CM\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow CD = CA\,\,\left( { = CM} \right)\,\,\,\,\left( {dpcm} \right).\)

