Cho đường tròn ( O ) và điểm A ở ngoài đường tròn. Các tiếp tuyến với

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) và điểm A ở ngoài đường tròn. Các tiếp tuyến với đường tròn \(\left( O \right)\) kẻ từ điểm A tiếp xúc với đường tròn \(\left( O \right)\) tại B và C. Trên đường tròn \(\left( O \right)\) lấy điểm M (khác với B và C) sao cho M và A nằm về 2 phía của đường thẳng BC. Từ M kẻ MH vuông góc với BC, MK vuông góc với AC và MI vuông góc với AB.
1) Chứng minh tứ giác MIBH nội tiếp.
2) Đường thẳng AM cắt đường tròn tại điểm thứ hai N. Chứng minh tam giác ABN đồng dạng với tam giác AMB, từ đó suy ra \(A{B^2} = AM.AN\).
3) Chứng minh: \(\angle MIH = \angle MHK\)
4) Chứng minh rằng \(MI + MK \ge 2MH\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
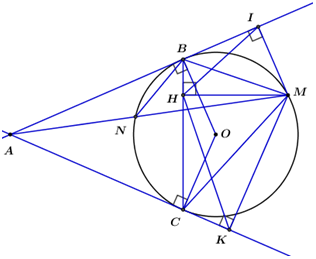
1) Chứng minh tứ giác MIBH nội tiếp.
Tứ giác MIBH có:
\(\begin{array}{l}\angle MHB = {90^o}\,\,\,\left( {MH \bot BC} \right)\\\angle MIB = {90^o}\,\,\,\,\left( {MI \bot AB} \right)\\ \Rightarrow \angle MHB + \angle MIB = {90^0} + {90^9} = {180^o}\end{array}\)
\( \Rightarrow \) Tứ giác MIBH nội tiếp. (dhnb) (đpcm)
2) Đường thẳng AM cắt đường tròn tại điểm thứ hai N. Chứng minh tam giác ABN đồng dạng với tam giác AMB, từ đó suy ra \(A{B^2} = AM.AN\).
Ta có AB là tiếp tuyến tại B của đường tròn \(\left( O \right)\) (gt)
\( \Rightarrow \angle ABN = \angle AMB\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BN)
Xét \(\Delta ABN\) và \(\Delta AMB\) có:
\(\begin{array}{l}\angle A\,\,chung\\\angle ABN = \angle AMB\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ABN \sim \Delta AMB\,\,\,\left( {g - g} \right) \Rightarrow \frac{{AB}}{{AM}} = \frac{{AN}}{{AB}}\\ \Rightarrow A{B^2} = AM.AN\,\,\,\left( {dpcm} \right).\end{array}\)
3) Chứng minh: \(\angle MIH = \angle MHK\)
Tứ giác MKCH có:
\(\begin{array}{l}\angle MHC = {90^o}\,\,\,\left( {MH \bot BC} \right)\\\angle MKC = {90^o}\,\,\,\left( {MK \bot AC} \right)\\ \Rightarrow \angle MHC + \angle MKC = {90^0} + {90^0} = {180^o}\end{array}\)
\( \Rightarrow \) Tứ giác MKCH nội tiếp. (dhnb)
\( \Rightarrow \angle MHK = \angle MCK\) (góc nội tiếp cùng chắn cung MK)
Mà \(\angle MCK = \angle MBC = \angle MBH\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung MC)
\(\angle MBH = \angle MIH\) (tứ giác MIBH nội tiếp, góc nội tiếp cùng chắn cung MH)
\( \Rightarrow \angle MIH = \angle MHK\) (đpcm)
4) Chứng minh rằng \(MI + MK \ge 2MH\)
Ta có: \(\angle MHI = \angle MBI\) (tứ giác MIBH nội tiếp, góc nội tiếp cùng chắn cung MI)
\(\angle MBI = \angle MCB = \angle MCH\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BM)
\(\angle MCH = \angle MKH\) (tứ giác MKCH nội tiếp, góc nội tiếp cùng chắn cung MH)
\( \Rightarrow \angle MHI = \angle MKH\,\,\,\left( { = \angle MCH} \right)\)
Xét \(\Delta MIH\) và \(\Delta MHK\) có:
\(\begin{array}{l}\angle MIH = \angle MHK\,\,\,\left( {cmt} \right)\\\angle MHI = \angle MKH\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MIH \sim \Delta MHK\,\,\left( {g - g} \right) \Rightarrow \frac{{MH}}{{MK}} = \frac{{MI}}{{MH}}\\ \Rightarrow MI.MK = M{H^2}.\end{array}\)
Áp dụng bất đẳng thức Cô-si ta được:
\(MI + MK \ge 2\sqrt {MI.MK} = 2\sqrt {M{H^2}} = 2MH\) (đpcm)

